15 страниц

‹ › ×

Устанавливает процедуры определения точечной и интервальной оценок медианы для любой совокупности случайных величин, описываемой непрерывной функцией распределения. Приведенные в стандарте методы не требуют знания функции распределения. Аналогичные процедуры могут применяться для определения оценок квартилей и других процентных точек распределения.

Скачать PDF

Дата введения	01.06.2004
Добавлен в базу	01.09.2013
Актуализация	01.01.2021

Раздел Строительство
- Раздел Стандарты
  - Раздел Другие государственные стандарты, применяемые в строительстве
    - Раздел 03 Социология. Услуги. Организация фирм и управление ими. Администрация. Транспорт

А также в:

Раздел Экология
- Раздел 03 СОЦИОЛОГИЯ. УСЛУГИ. ОРГАНИЗАЦИЯ ФИРМ И УПРАВЛЕНИЕ ИМИ. АДМИНИСТРАЦИЯ. ТРАНСПОРТ
  - Раздел 03.120 Качество
    - Раздел 03.120.20 Сертификация продукции и фирм. Оценка соответствия

А также в:

Раздел Электроэнергия
- Раздел 03 СОЦИОЛОГИЯ. УСЛУГИ. ОРГАНИЗАЦИЯ ФИРМ И УПРАВЛЕНИЕ ИМИ. АДМИНИСТРАЦИЯ. ТРАНСПОРТ
  - Раздел 03.120 Качество
    - Раздел 03.120.20 Сертификация продукции и фирм. Оценка соответствия

Организации:

27.01.2004	Утвержден	Госстандарт России	34-ст
	Разработан	ТК 125 Статистические методы в управлении качеством продукции
	Издан	ИПК Издательство стандартов	2004 г.

Statistical methods. Statistical interpretation of data. Median. Estimation and confidence intervals

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ ПО СТАНДАРТИЗАЦИИ И МЕТРОЛОГИИ

ГОСТ Р исо

16269-7—

2004

НАЦИОНАЛЬНЫЙ

СТАНДАРТ

РОССИЙСКОЙ

ФЕДЕРАЦИИ

Статистические методы

СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ.

МЕДИАНА

Определение точечной оценки и доверительных интервалов

ISO 16269-7:2001 Statistical interpretation of data —

Part 7: Median — Estimation and confidence intervals (IDT)

Издание официальное

Москва ИПК Издательство стандартов 2004

ГОСТ Р ИСО 16269-7-2004

Предисловие

1 ПОДГОТОВЛЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» на основе собственного аутентичного перевода стандарта, указанного в пункте 4

2 ВНЕСЕН Научно-техническим управлением Госстандарта России

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 27 января 2004 г. № 34-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 16269-7-2001. «Статистическое представление данных. Часть 7. Медиана. Определение точечной оценки и доверительных интервалов» (ISO 16269-7:2001 «Statistical interpretation of data — Part 7: Median — Estimation and confidence intervals»)

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5 (подраздел 3.6).

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении С

5 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в указателе «Национальные стандарты», а текст этих изменений — в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе «Национальные стандарты»

Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Госстандарта России

ГОСТ Р ИСО 16269-7-2004

Содержание

1 Область применения................................................................. 1

2 Нормативные ссылки................................................................. 1

3 Термины, определения и обозначения.................................................. 1

4 Условия применения................................................................. 2

5 Определение точечной оценки......................................................... 2

6 Определение доверительного интервала................................................ 2

Приложение А (справочное) Классический метод определения границ доверительных интервалов для

медианы............................................................... 7

Приложение В (справочное) Примеры определения доверительных границ.................... 8

Приложение С (справочное) Сведения о соответствии национальных стандартов Российской Федерации ссылочным международным стандартам...............................11

ГОСТ Р ИСО 16269-7-2004

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Статистические методы

СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ. МЕДИАНА

Определение точечной оценки и доверительных интервалов

Statistical methods. Statistical interpretation of data. Median. Estimation and confidence intervals

Дата введения — 2004—06—01

1 Область применения

Настоящий стандарт устанавливает процедуры определения точечной и интервальной оценок медианы для любой совокупности случайных величин, описываемой непрерывной функцией распределения. Приведенные в стандарте методы не требуют знания функции распределения. Аналогичные процедуры могут применяться для определения оценок квартилей и других процентных точек распределения.

Примечание — Медиана — 50 %-мая точка распределения,

2 Нормативные ссылки

В настоящем стандарте использована ссылка на следующий стандарт:

ИСО 3534-1:1993 Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основные статистические термины.

3 Термины, определения и обозначения

3.1 Термины и определения

В настоящем стандарте применены термины по ИСО 3534-1. а также следующие термины с соответствующими определениями:

3.1.1 А-я порядковая статистика выборки (A-th order statistic of a sample):

Значение А-го элемента выборки, когда все элементы выборки расположены в таком порядке, при котором каждый последующий элемент выборки более или равен (не менее) предыдущему (порядок неубывания).

Примечание — Для выборки из п элементов, расположенных в порядке неубывания Ц,| < £ ... £ ).

к-й порядковой статистикой является элемент

3.1.2 медиана непрерывного распределения (median of a continuous probability distribution): Такая величина, когда каждая из долей распределения, лежащих по обе стороны от нее. равна 0,5.

Примечание — В настоящем стандарте для медианы непрерывного распределения применен термин «медиана совокупности» и обозначен буквой М.

3.2 Обозначения

В настоящем стандарте применены следующие обозначения:

/1 — нижняя граница значений случайной величины в совокупности: b — верхняя граница значений случайной величины в совокупности;

Издание официальное

ГОСТ Р ИСО 16269-7-2004

С — уровень доверия;

с — постоянная, используемая для определения величины к в уравнении (1); к — номер порядковой статистики, используемый для определения нижней доверительной границы;

М — медиана совокупности;

N — объем выборки;

7', — нижняя доверительная граница, рассчитанная по выборке;

7*2 — верхняя доверительная граница, рассчитанная по выборке;

0 — квантиль стандартного нормального распределения;

^ХИ “ элемент выборки, когда элементы выборки расположены в порядке неубывания (каждый последующий элемент ряда более или равен предыдущему); х — выборочное значение медианы (оценка медианы, рассчитанная по выборочным данным); у — значение промежуточных вычислений при определении величины к (см. уравнение (1)).

4 Условия применения

Метод, описанный в настоящем стандарте, применим при выполнении следующих условий:

- генеральная совокупность описывается непрерывной функцией распределения;

- выборка составляется случайным образом.

Примечание — Для случаев, когда распределение совокупности может быть описано нормальным распределением, медиана совокупности совпадает с математическим ожиданием. В этом случае могут применяться методы определения доверительных границ для математического ожидания совокупности.

5 Определение точечной оценки

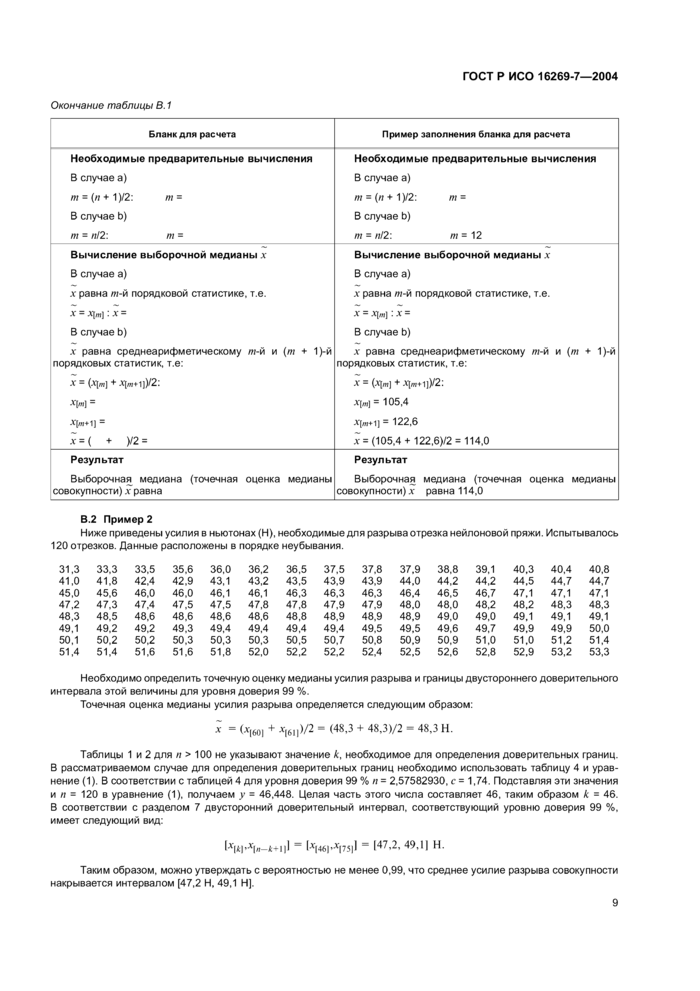
Точечной оценкой медианы совокупности является выборочная медиана х. Для определения выборочной медианы все элементы выборки необходимо расположить в порядке их неубывания. Выборочная медиана х равна:

х, , — если л нечетное число;

*♦ I

х *

— порядковая статистика с номером

Л+ 1

2 ^:

Примечани е —Данная оценка в общем случае для несимметричных распределений является смещенной. При этом не существует метода определения несмещенной оценки для любых непрерывных распределений.

6 Определение доверительного интервала

6.1 Общие положения

Двусторонний доверительный интервал для медианы — это закрытый интервал (7‘,. Т₂], где 7', < Т₂. а /', и Т₂ — соответственно нижняя и верхняя доверительные границы.

ГОСТ Р ИСО 16269-7-2004

Если а и Ь — соответственно нижняя и верхняя границы значений случайной величины в генеральной совокупности, то односторонние доверительные интервалы, соответственно, имеют вид [Т_л, Ь) и (a, 7у.

Примечание — На практике часто значение а принимают равным нулю для положительных переменных, а для переменных, не имеющих естественной верхней границы, в качестве b принимают бесконечность.

Практическое значение применения доверительного интервала состоит в том, что исследователь может определить интервал, накрывающий неизвестное значение медианы совокупности М. Причем вероятность противоположного события (интервал не накрывает М) не превышает назначенного малого значения. Вероятность того, что доверительный интервал накрывает медиану совокупности, называется доверительной вероятностью.

6.2 Классический метод

Классический метод определения границ доверительного интервала для медианы совокупности приведен в приложении А Метод включает решение двух неравенств. Альтернативные методы определения границ доверительного интервала для некоторых значений уровня доверия приведены ниже.

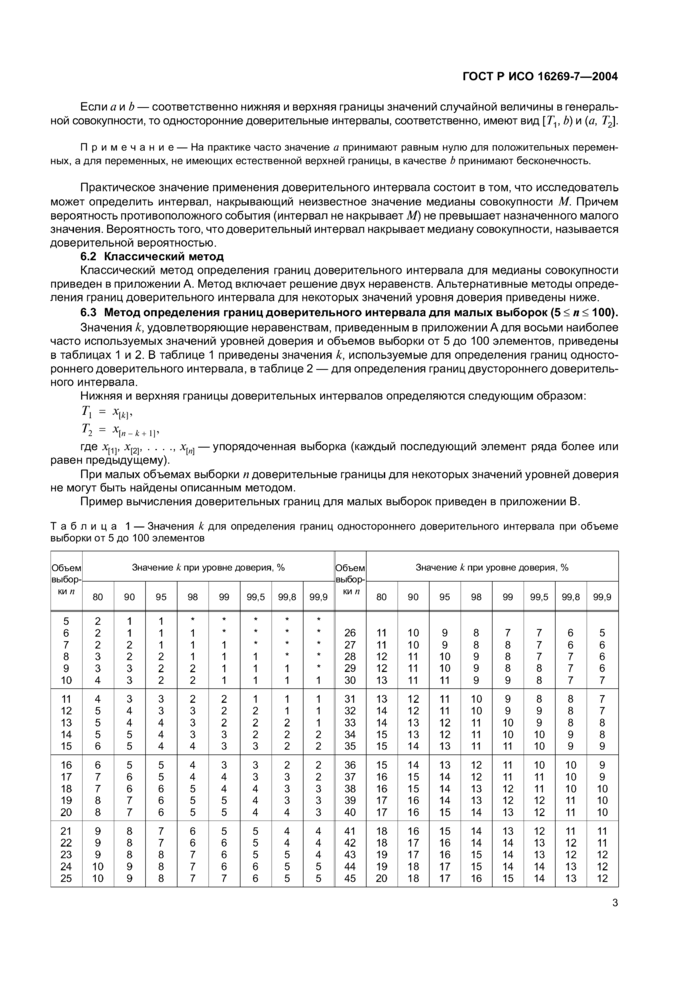
6.3 Метод определения границ доверительного интервала для малых выборок (5 < л ? 100).

Значения к, удовлетворяющие неравенствам, приведенным в приложении А для восьми наиболее

часто используемых значений уровней доверия и объемов выборки от 5 до 100 элементов, приведены в таблицах 1 и 2. В таблице 1 приведены значения к, используемые для определения границ одностороннегодоверительного интервала, в таблице 2 — для определения границ двустороннего доверительного интервала.

Нижняя и верхняя границы доверительных интервалов определяются следующим образом:

'2 ~ ^х|в-*« ||*

где х_[2]......лг_(п, — упорядоченная выборка (каждый последующий элемент ряда более или

равен предыдущему).

При малых объемах выборки «доверительные границы для некоторых значений уровней доверия не могут быть найдены описанным методом.

Пример вычисления доверительных границ для малых выборок приведен в приложении В.

Таблица 1— Значения к для определения границ одностороннего доверительного интервала при объеме выборки от 5 до 100 элементов

Обьем пыбор-	Змачо**ю к при уровне доверия Ч								Обьем выбор-	Значение к при уровне доверия. %
ни п	80	90	95	98	99	99.5	99.8	99.9	ки п	80	90	95	98	99	99.5	99.8	99.9
5	2	1	1	•	•	•	•	•
6	2	1	1	1	•	•	•	•	26	11	10	9	8	7	7	6	5
7	2	2	1	1	1	•	•	•	27	11	10	9	8	8	7	6	6
8	3	2	2	1	1	1	•	•	28	12	11	10	9	8	7	7	6
9	з	3	2	2	1	1	1	•	29	12	11	10	9	8	8	7	6
10	4	3	2	2	1	1	1	1	30	13	11	11	9	9	8	7	7
11	4	3	3	2	2	1	1	1	31	13	12	11	10	9	8	8	7
12	5	4	3	3	2	2	1	1	32	14	12	11	10	9	9	8	7
13	5	4	4	3	2	2	2	1	33	14	13	12	11	10	9	8	8
14	5	5	4	3	3	2	2	2	34	15	13	12	11	10	10	9	8
15	6	5	4	4	3	3	2	2	35	15	14	13	11	11	10	9	9
16	6	5	5	4	3	3	2	2	36	15	14	13	12	11	10	10	9
17	7	6	5	4	4	3	3	2	37	16	15	14	12	11	11	10	9
18	7	6	6	5	4	4	3	3	38	16	15	14	13	12	11	10	10
19	8	7	6	5	5	4	3	3	39	17	16	14	13	12	12	11	10
20	8	7	6	5	5	4	4	3	40	17	16	15	14	13	12	11	10
21	9	8	7	6	5	5	4	4	41	18	16	15	14	13	12	11	11
22	9	8	7	6	6	5	4	4	42	18	17	16	14	14	13	12	11
23	9	8	8	7	6	5	5	4	43	19	17	16	15	14	13	12	12
24	10	9	8	7	6	6	5	5	44	19	18	17	15	14	14	13	12
25	10	9	8	7	7	6	5	5	45	20	18	17	16	15	14	13	12

ГОСТ Р ИСО 16269-7-2004

Окончание таблицы 1

Объем выбор-	Значение к при уровне доверия. %								Объем	Змачс*мо к при уровне доверия %
--Т- ки п	80	90	95	98	99	99.5	998	99,9	ки я	80	90	95	98	99	99.5	99.8	999
46	20	19	17	16	15	14	13	13	76	34	32	31	29	28	27	26	25
47	21	19	18	17	16	15	14	13	77	35	33	31	30	28	27	26	25
48	21	20	18	17	16	15	14	13	78	35	33	32	30	29	28	26	25
49	22	20	19	17	16	16	15	14	79	36	34	32	30	29	28	27	26
50	22	20	19	18	17	16	15	14	80	36	34	33	31	30	29	27	26
51	22	21	20	18	17	16	15	15	81	37	35	33	31	30	29	28	27
52	23	21	20	19	18	17	16	15	82	37	35	34	32	31	29	28	27
53	23	22	21	19	18	17	16	15	83	38	36	34	32	31	30	28	28
54	24	22	21	19	19	18	17	16	84	38	36	34	33	31	30	29	28
55	24	23	21	20	19	18	17	16	85	39	37	35	33	32	31	29	28
56	25	23	22	20	19	18	17	17	86	39	37	35	33	32	31	30	29
57	25	24	22	21	20	19	18	17	87	40	38	36	34	33	32	30	29
58	26	24	23	21	20	19	18	17	88	40	38	36	34	33	32	31	30
59	26	25	23	22	21	20	19	18	89	41	38	37	35	34	32	31	30
60	27	25	24	22	21	20	19	18	90	41	39	37	35	34	33	31	30
61	27	25	24	23	21	21	19	19	91	41	39	38	36	34	33	32	31
62	28	26	25	23	22	21	20	19	92	42	40	38	36	35	34	32	31
63	28	26	25	23	22	21	20	19	93	42	40	39	37	35	34	33	32
64	29	27	25	24	23	22	21	20	94	43	41	39	37	36	35	33	32
65	29	27	26	24	23	22	21	20	95	43	41	39	38	36	35	34	33
66	30	28	26	25	24	23	21	21	96	44	42	40	38	37	35	34	33
67	30	28	27	25	24	23	22	21	97	44	42	40	38	37	36	34	33
68	31	29	27	26	24	23	22	21	98	45	43	41	39	38	36	35	34
69	31	29	28	26	25	24	23	22	99	45	43	41	39	38	37	35	34
70	31	30	28	26	25	24	23	22	100	46	44	42	40	38	37	36	35
71	32	30	29	27	26	25	23	23
72	32	31	29	27	26	25	24	23
73	33	31	29	28	27	26	24	23
74	33	31	30	28	27	26	25	24
75	34	32	30	29	27	26	25	24

• Доверительные границы не могут быть определены для данного уровня доверия и данного объема выборки.

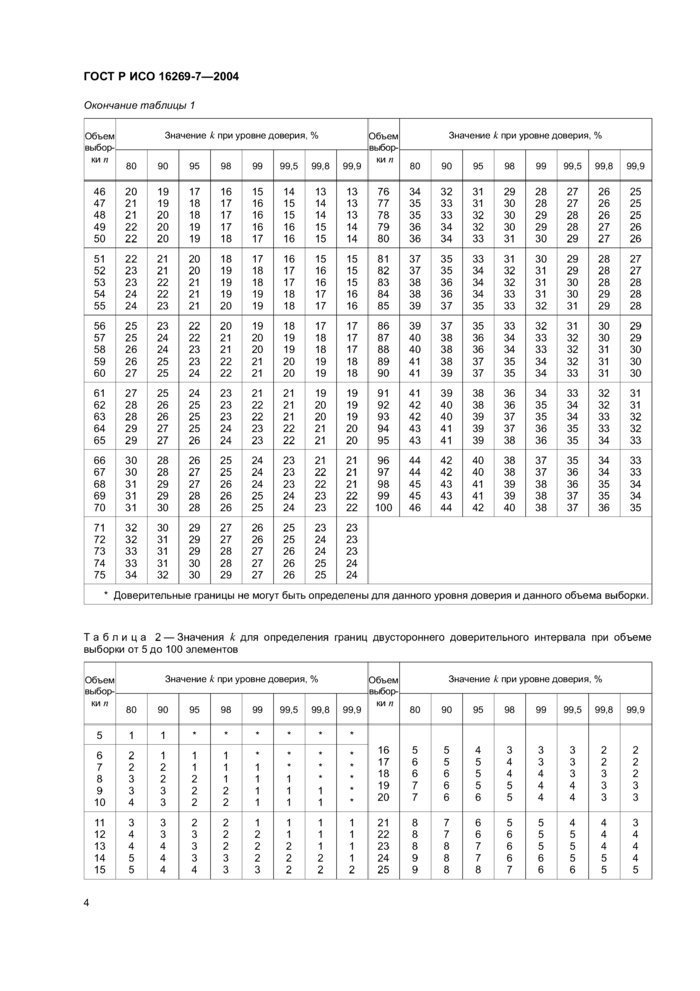
Таблица 2 — Значения А для определения границ двустороннего доверительного интервала при объеме выборки от 5 до 100 элементов

Объем выбор-	Значение к при уровне доверия. % _								Объем	Значение к при уровне доверия. %
ки л	80	90	95	98	99	99.5	99.8	99.9	ки я	80	90	95	98	99	99,5	99.8	99.9
5	1	1	•	•	•	•	•	•
6	2	1	1	1	•	•	•	•	16	5	5	4	3	3	3	2	2
7	2	2	1	1	1	•	•	•	17	6	5	5	4	3	3	2	2
8	3	2	2	1	1	1	•	•	18	6	6	5	4	4	3	3	2
9	3	3	2	2	1	1	1	•	19	7	6	5	5	4	4	3	3
10	4	3	2	2	1	1	1	•	20	7	6	6	5	4	4	3	3
11	3	3	2	2	1	1	1	1	21	8	7	6	5	5	4	4	3
12	4	3	3	2	2	1	1	1	22	8	7	6	6	5	5	4	4
13	4	4	3	2	2	2	1	1	23	8	8	7	6	5	5	4	4
14	5	4	3	3	2	2	2	1	24	9	8	7	6	6	5	5	4
15	5	4	4	3	3	2	2	2	25	9	8	8	7	6	6	5	5

ГОСТ Р ИСО 16269-7-2004

Окончание табпицы 2

Обьем выбор-	Значение к при уровне доверия. %								Обьем выбор-	Значение к при уровне доверия. %
ни п	80	90	95	98	99	99.5	99.8	99.9	КИ л	80	90	95	98	99	99.5	99.8	99.9
26	10	9	8	7	7	6	5	5	66	28	26	25	24	23	22	21	20
27	10	9	8	8	7	6	6	5	67	28	27	26	24	23	22	21	20
28	11	10	9	8	7	7	6	6	68	29	27	26	24	23	23	21	21
29	11	10	9	8	8	7	6	6	69	29	28	26	25	24	23	22	21
30	11	11	10	9	8	7	7	6	70	30	28	27	25	24	23	22	21
31	12	11	10	9	8	8	7	7	71	30	29	27	26	25	24	23	22
32	12	11	10	9	9	8	7	7	72	31	29	28	26	25	24	23	22
33	13	12	11	10	9	9	8	7	73	31	29	28	27	26	25	23	23
34	13	12	11	10	10	9	8	8	74	31	30	29	27	26	25	24	23
35	14	13	12	11	10	9	9	8	75	32	30	29	27	26	25	24	23
36	14	13	12	11	10	10	9	8	76	32	31	29	28	27	26	25	24
37	15	14	13	11	11	10	9	9	77	33	31	30	28	27	26	25	24
38	15	14	13	12	11	10	10	9	78	33	32	30	29	28	27	25	25
39	16	14	13	12	12	11	10	9	79	34	32	31	29	28	27	26	25
40	16	15	14	13	12	11	10	10	80	34	33	31	30	29	28	26	25
41	16	15	14	13	12	12	11	10	81	35	33	32	30	29	28	27	26
42	17	16	15	14	13	12	11	11	82	35	34	32	31	29	28	27	26
43	17	16	15	14	13	12	12	11	83	36	34	33	31	30	29	28	27
44	18	17	16	14	14	13	12	11	84	36	34	33	31	30	29	28	27
45	18	17	16	15	14	13	12	12	85	37	35	33	32	31	30	28	27
46	19	17	16	15	14	14	13	12	86	37	35	34	32	31	30	29	28
47	19	18	17	16	15	14	13	12	87	38	36	34	33	32	30	29	28
48	20	18	17	16	15	14	13	13	88	38	36	35	33	32	31	30	29
49	20	19	18	16	16	15	14	13	89	38	37	35	34	32	31	30	29
50	20	19	18	17	16	15	14	14	90	39	37	36	34	33	32	30	30
51	21	20	19	17	16	16	15	14	91	39	38	36	34	33	32	31	30
52	21	20	19	18	17	16	15	14	92	40	38	37	35	34	33	31	30
53	22	21	19	18	17	16	15	15	93	40	39	37	35	34	33	32	31
54	22	21	20	19	18	17	16	15	94	41	39	38	36	35	33	32	31
55	23	21	20	19	18	17	16	15	95	41	39	38	36	35	34	33	32
56	23	22	21	19	18	18	17	16	96	42	40	38	37	35	34	33	32
57	24	22	21	20	19	18	17	16	97	42	40	39	37	36	35	33	32
58	24	23	22	20	19	18	17	17	98	43	41	39	38	36	35	34	33
59	25	23	22	21	20	19	18	17	99	43	41	40	38	37	36	34	33
60	25	24	22	21	20	19	18	17	100	44	42	40	38	37	36	35	34
61	25	24	23	21	21	20	19	18
62	26	25	23	22	21	20	19	18
63	26	25	24	22	21	20	19	19
64	27	25	24	23	22	21	20	19
65	27	26	25	23	22	21	20	19

* Доверительные границы не могут быть определены для данного уровня доверия и данного объема выборки.

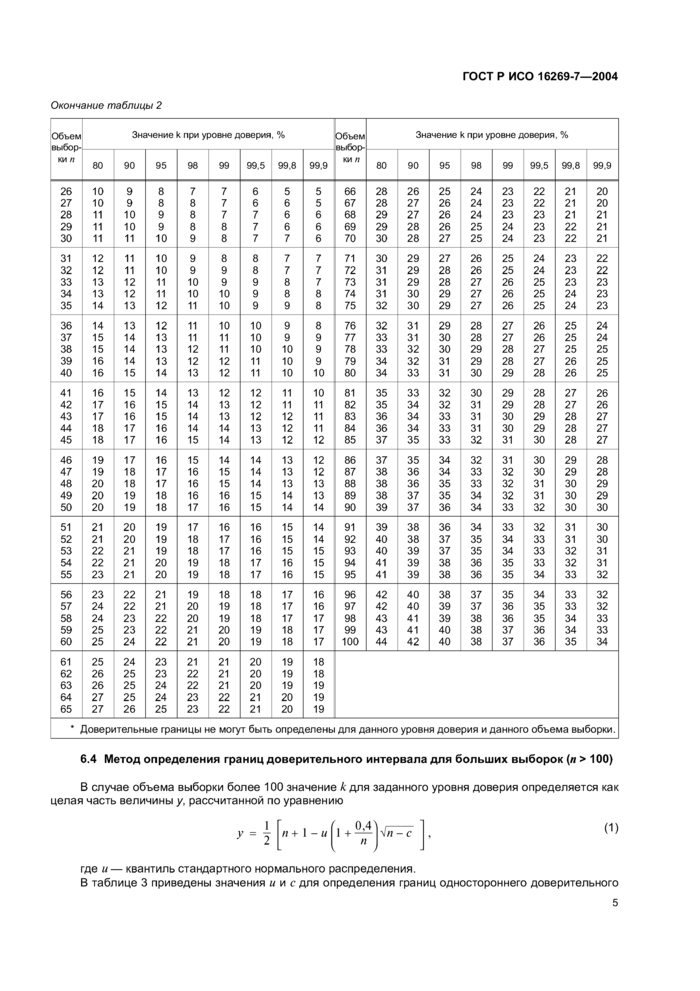
6.4 Метод определения границ доверительного интервала для больших выборок (я > 100)

В случае объема выборки более 100 значение к для заданного уровня доверия определяется как целая часть величины у, рассчитанной по уравнению

(1)

где и — квантиль стандартного нормального распределения.

В таблице 3 приведены значения и и с для определения границ одностороннего доверительного

ГОСТ Р ИСО 16269-7-2004

интервала. В таблице 4 приведены значения и и г для определения границ двустороннего доверительного интервала.

Таблица 3 — Значения и и с для определения границ одностороннего доверительного интервала

Уровень доверия, %	Значение и	Значение с
80.0	0.841 621 22	0.7500
90.0	1.281 551 56	0.9030
95,0	1,644 853 64	1.0870
98.0	2.053 748 92	1.3375
99.0	2.326 347 88	1.5360
99.5	2.575 829 30	1.7400
99.8	2,878 161 73	2.0140
99.9	3,090 232 29	2.2220

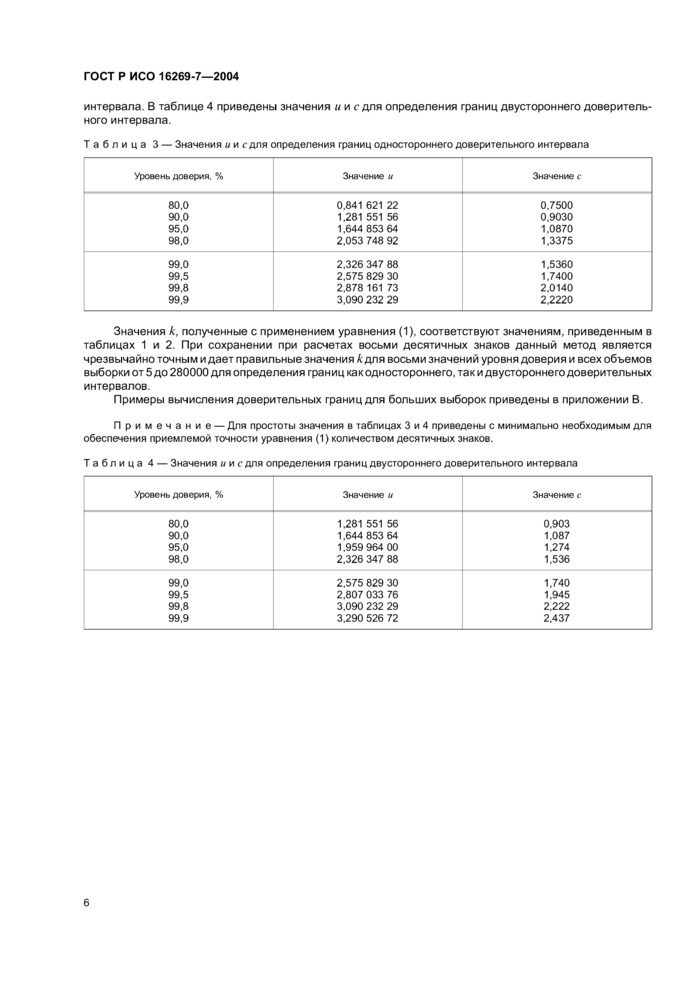
Значения к, полученные с применением уравнения (1), соответствуют значениям, приведенным в таблицах 1 и 2. При сохранении при расчетах восьми десятичных знаков данный метод является чрезвычайно точным и дает правильные значения к для восьми значений уровня доверия и всех объемов выборки от 5 до 280000 для определения гран иц ка к одностороннего, так и двустороннего доверительных интервалов.

Примеры вычисления доверительных границ для больших выборок приведены в приложении В.

Примечание — Для простоты значения в таблицах 3 и 4 приведены с минимально необходимым для обеспечения приемлемой точности уравнения (1) количеством десятичных знаков.

Таблица 4 — Значения миг для определения границ двустороннего доверительного интервала

Уровень доверия, %	Значение и	Значение с
80.0	1.281 551 56	0.903
90,0	1,644 853 64	1,087
95.0	1.959 964 00	1.274
98,0	2.326 347 88	1.536
99,0	2.575 829 30	1.740
99,5	2,807 033 76	1,945
99,8	3.090 232 29	2.222
99.9	3,290 526 72	2.437

ГОСТ Р ИСО 16269-7-2004

Приложение А (справочное)

Классический метод определения границ доверительных интервалов для медианы

Предположим, что выборка объема п выбрана случайным образом из непрерывной генеральной совокупности. Тогда вероятность того, что точно к выборочных значений будут менее медианы совокупности, описывается биномиальным распределением:

Это является также и вероятностью того, что точно к выборочных значений будут более медианы совокупности.

Нижней и верхней границами двустороннего доверительного интервала, соответствующего доверительной вероятности (1 - а), являются достаточные статистики и х^_я t.,| соответственно. Значение величины к должно удовлетворять следующим неравенствам:

то есть

(А.2)

(АЗ)

(А 4)

При определении границ одностороннего доверительного интервала в уравнениях (А.1) — (А.4) необходимо заменить а/2 на а.

ГОСТ Р ИСО 16269-7-2004
Статистические методы. Статистическое представление данных. Медиана. Определение точечной оценки и доверительных интервалов

Оглавление

Этот ГОСТ находится в:

Организации:

Statistical methods. Statistical interpretation of data. Median. Estimation and confidence intervals

ГОСТ Р ИСО 16269-7-2004Статистические методы. Статистическое представление данных. Медиана. Определение точечной оценки и доверительных интервалов

Оглавление

Этот ГОСТ находится в:

Организации:

Statistical methods. Statistical interpretation of data. Median. Estimation and confidence intervals

Статистические методы

СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ.

МЕДИАНА

Определение точечной оценки и доверительных интервалов

ГОСТ Р ИСО 16269-7-2004

1 Область применения

2 Нормативные ссылки

3 Термины, определения и обозначения

4 Условия применения

5 Определение точечной оценки

6 Определение доверительного интервала

ГОСТ Р ИСО 16269-7-2004
Статистические методы. Статистическое представление данных. Медиана. Определение точечной оценки и доверительных интервалов