ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
ГОСТ 11.007-75
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ СОВЕТА МИНИСТРОВ СССР
Москва
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
ГОСТ 11.007-75
Издание официальное
ГОСТ 11.007-75 Стр. 9
|
Продолжение табл. 2 |
|
Объем выборки п |
|
г, |
4 |
|
|
|
3 |
|
|
V 1=0,75 |
Vi=0,90 |
Yi=o,95 |
Vi=0,98 |
Y2=0,75 |
72=0,90 |
7,=0,95 |
7*=0,93 |
|
16 |
1,223 |
1,406 |
1,535 |
1,693 |
0,926 |
0,826 |
0,775 |
0,723 |
|
17 |
1,213 |
1,388 |
1,510 |
1,660 |
0,927 |
0,829 |
0,779 |
, 0,728 |
|
18 |
1,204 |
1,371 |
1,487 |
1,630 |
0,927 |
0,832 |
0,784 |
0,734 |
|
19 |
1,196 |
1,356 |
1,467 |
1,603 |
0,928 |
0,835 |
0,788 |
0,739 |
|
20 |
1,188 |
1,343 |
1,449 |
1,579 |
0,929 |
0,838 |
0,791 |
0,743 |
|
22 |
1,176 |
1,320 |
1,418 |
1,538 |
0,930 |
0,843 |
0,798 |
0,752 |
|
24 |
1,165 |
1,301 |
1,392 |
1,504 |
0,932 |
0,848 |
0,805 |
0,759 |
|
26 |
1,156 |
1,284 |
1,370 |
1,475 |
0,933 |
0,852 |
0,810 |
0,766 |
|
’28 |
1,148 |
1,269 |
1,351 |
1,450 |
0,934 |
0,856 |
0,815 |
0,772 |
|
30 |
1,141 |
1,257 |
1,334 |
1,429 |
0,935 |
0,860 |
0,820 |
0,778 |
|
32 |
1,135 |
1,246 |
1,319 |
1,409 |
0,937 |
0,863 |
0,824 |
0,783 |
|
34 |
1,129 |
1,236 |
1,306 |
1,392 |
0,938 |
0,866 |
0,828 |
0,788 |
|
36 |
1,125 |
1,227 |
1,294 |
1,377 |
0,939 |
0,869 |
0,832 |
0,793 |
|
38 |
1,120 |
1,219 |
1,283 |
1,363 |
0,940 |
0,872 |
0,835 |
0,797 |
|
40 |
1,116 |
1,211 |
1,273 |
1,351 |
0,940 |
0,875 |
0,839 |
0,801 |
|
42 |
1,112 |
1,204 |
1,265 |
1,339 |
0,941 |
0,877 |
0,842 |
0,804 |
|
44 |
1,109 |
1,198 |
1,256 |
1,329 |
0,942 |
0,880 |
0,845 |
0,808 |
|
46 |
1,106 |
1,192 |
1,249 |
1,319 |
0,943 |
0,882 |
0,847 |
0,811 |
|
48 |
1,103 |
1,187 |
1,242 |
1,310 |
0,944 |
0,884 |
0,850 |
0,814 |
|
50 |
1,100 |
1,182 |
1,235 |
1,301 |
0,944 |
0,886 |
0,852 |
0,817 |
|
52 |
1,098 |
1,177 |
1,229 |
1,294 |
0,945 |
0,888 |
0,854 |
0,820 |
|
54 |
1,095 |
1,173 |
1,224 |
1,286 |
0,946 |
0,890 |
0,857 |
0,822 |
|
56 |
1,093 |
1,169 |
1,218 |
1,280 |
0,946 |
0,891 |
0,859 |
0,825 |
|
58 |
1,091 |
1,165 |
1,213 |
1,273 |
0,947 |
0,893 |
0,861 |
0,827 |
|
60 |
1,089 |
1,162 |
1,208 |
1,267 |
0,948 |
0,894 |
0,863 |
0,830 |
|
62 |
1,087 |
1,158 |
1,204 |
1,262 |
0,948 |
0,896 |
0,864 |
0,832 |
|
64 |
1,086 |
1,155 |
1,200 |
1,256 |
0,949 |
0,897 |
0,866 |
0,834 |
|
66 |
1,084 |
1,152 |
1,196 |
1,251 |
0,949 |
0,899 |
0,868 |
0,836 |
|
68 |
1,083 |
1,149 |
1,192 |
1,246 |
0,950 |
0,900 |
0,869 |
0,838 |
|
70 |
1,081 |
1,146 |
1,188 |
1,242 |
0,950 |
0,901 |
0,871 |
0,840 |
|
72 |
1,080 |
1,144 |
1,185 |
1,237 |
0,951 |
0,903 |
0,872 |
0,841 |
|
74 |
1,078 |
1,141 |
1,182 |
1,233 |
0,951 |
0,904 |
0,874 |
0,843 |
|
76 |
1,077 |
1,139 |
1,179 |
1,229 |
0,952 |
0,905 |
0,875 |
0,845 |
|
78 |
1,076 |
1,136 |
1,176 |
1,225 |
0,952 |
0,906 |
0,876 |
0,846 |
|
80 |
1,075 |
1,134 |
1,173 |
1,222 |
0,952 |
0,907 |
0,878 |
0,848 |
|
85 |
1,072 |
1,129 |
1,166 |
1,213 |
0,953 |
0,910 |
0,881 |
0,852 |
|
90 |
1,069 |
1,124 |
1,160 |
1,206 |
0,954 |
0,912 |
0,883 |
0,855 |
|
95 |
1,067 |
1,120 |
1,155 |
1,199 |
0,955 |
0,914 |
0,886 |
0,858 |
|
100 |
1,065 |
1,116 |
1,150 |
1,192 |
0,956 |
0,916 |
0,888 |
0,861 |
|
110 |
1,062 |
1,110 |
1,141 |
1,181 |
0,958 |
0,920 |
0,893 |
0,866 |
|
420 |
1,058 |
1,104 |
1,133 |
1,171 |
0,959 |
0,923 |
0,897 |
0,871 |
|
Op. 10 ГОСТ 11.007-75
|
Значения |
|
|
00
сл
1 |
^cooo^Ooc^Oco^^OooapoocoO^oqpTt-'CNiOOOt—'Coio COOOHOION^qD-<001Л<МСГ|Ь-1Л'^чО00СО'ФсдОО^00^СС>Ю'фС¥5<М
О СО ^ О О 00 00 t'-* CD СО СОЮ 1ЛЮ 1Л Й ^ со со со со со со со со —^ _Г —Г o' О О О О" о сГ o' о o' о o' о о" o' o'1 o' o' o' o' о" о" o' o' о" о
1 III 1 ITIII ITI ITI 1 1 1 111 ITI 1 ITI t |
|
|
ю
сл
1 |
—|l0’^00^tH,,^NC^00C0l^i0CD00OC0C0O ^t4Or-'CO’—lOCMOQLOcOOGOt^LO^fCNOOOCDLOCOCg—<OCnoOOOt--CDCD C\|O^NNc£3i£)l^lOiCL0'^'^^T:tl''t'^00r0C0C0000000CNOlCviOl(N(>l |
|
ffl
N |
£ |
*-i -H о o' о о о" о о о' о о о о" о" О о о' о o' о" о' о" o' о" О o' о С?" о*
И 1 1 ! 1 1 1 II N II 1 1 1 1 1 Т II i II 7 i 1 7 1 |
|
|
§
о
'L |
000{N—•OOoOOLOOOCMCsi'^OO^h’^-'^CDOO^— -^ООСОООСО .30 ^tlOOi'tONlOCs)-'OiN0lOTtfO'*<aoONCDlO'tCOrO(N — -lOO OOt^OLOlO^^'^',^'^OCOOOCOCOCOCOCN)CNCvlCStOjCN<NCNCSt(NCSI<N<N |
|
|
|
О СГ О О ООО о о о о о о о о о o' o' о o' о' о" о" о о о" o’ о о' о"
1 Т 1 М 1 1 II II II 1 1 II 1 II 1 1 1 1 II 1 1 1 1 |
|
|
£
о
II,
£ |
^ю^соспоооаоо^орооо -HiotDooo'tai'^aiw — ooccMMOuo 00 ’—1 ОО CD LQ СО Cs| О О О 00 b~ CD Ю СО СО СО CN CS) С\) '—> »—1 ’—' О О ^COOOO-JC'-'ICsiC'sjC4-) СЧ СМ СМ ’—1 00 г~‘ '—’ ’—1 ’—’—1 ’—1 •—1 '—' 1—1 1—< д—1 — у-i ^
o' о“ o' o' о“ о" o' о' о” о'’ о' cf о ~ o' о о' о' o’ о" о о” o' o’ о” o'1 о” о о' o'"
1 I 1 1 1 1 1 1 1 I J ! 1 <j> 1 1 i 1 1 1 1 J 1 1 J 1 1 1 1 1 |
|
|
00
сл
о*
11^ |
(NWOcON^NW^^WN^^CCOlSSwCOinoOCOlM^-HW^CO OOffilMO - ЛОЮ^ООКХМОоОЮ^ип'ф^^^МООЮОЬЩЮ^СО ЮС^^О0^00Ь^КС0ОС0С01бЮ1Л^ "’^^^^^Г0с0С0С0С,0Г000
~ —Г ^ о o' o' o' o' o' o' o' o' o' o' o' ° о o' o' o' o' o' o' o' o' o' o' o' |
|
|
£ |
|
|
иэ
О)
f |
ка)01-н^^ю^т1'0050гоьсо-оосп<мьт1-сос1(мсо1лоогн^оо OCO(MWOi^ON't(MO36?)CD'tCOCSig)N0^mCN-ЮФСОМ^ФЮ 05 00 N 0 CD CD Ю Ю Ю ^ «Ф ^ Tt со СО СО СО СО ГО CO CO (N (N CS| C^l (N |
|
|
|
—Г o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' |
|
|
§
о
£ |
(N<D00NNiO00lOCDOl’tO00000000(M00C£ll0cDNa5CMC0O't(b^C) Ncn^TfON Tf CN О OO CD CO CM ’—1 О 00 N tD LQ Tf f0 OQ C-) <M ■—'ООО N CD ю 1б Ю Tl- тг ^ CO w со C3 СО О СЧ СЧ CSIr w W (N W (N W (N CSJ «
Q o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' о о' о' о' о о о' о' о' о' |
|
|
ю
о'
й,
£ |
О (М CN >—<LO(Ni—iW't ЬОЮСЮ-'ЬО^СО^СЛЮ^ООЮГО OqpiOCO -ФОб-ЮОСО—OOOOOOb-r-COCOir>lO^OOOCS|CM^~~. — -—ООО СОСОСМ(МС^<М<МС^^^—^—‘ ^ ^ ^ ^"1 — —^ ~ ~ ~“L о' о о' о о о' о' о' о' о' о' о' о' О О о' о о' о' о о' О ООО о' о' о' о |
|
Объем выборки п |
о—i(NC0-^,L0CCt^00aiOCMrt4CD0QOCN'^C000OCS|T^C000 |
|
00-^0с0000с0о001''--10см0а010с0а0т^сг>с00с0
OOOOOOOb-r'^l''-t''--CO<OCOcOlOLOlO^''t,COCOCMCM
т^СМОООО^сМ’—1idGOtOtA’^CO’—'C^QOlOCOi—• Г"- ’'f oOocr>a>o^ajoioooogpQDoocooo®bh-Nh-co<£) ^ °„0„0 2 0 Ooooos OO OOO^CSOO Cf o' o' О o' o' о d o’ o' o' o' o' О o' o'" о о о' о о" о"
I I I I I II I I 1 и I I I I I II I II
QO-HlOO)CON(NN(No0^05(D(MOOlOCOCi(N(D^lO (NC^-.OOa)0)OOoOh-NOtOtDWWTt'COCO(N^O « CO CO 00 СО СЧ « N « w CM CM CM CM CM CM CM CM CM CMCM CM^
o' o' o' o' o' o' o' o' o' O' o' o' o' o' o' o' o' o' o' o' o' o'
«NcOOOCOO)lO-OO^^OOlCC)CDNOLOCDlCCDffi Ю'^’^СОСОСМСМСМ^—'гнОООСО)СоО^ЬСОЮ CM^CN CM CM CM CM 04 CM CM CM CM CM CM <N ~ ~ ~ ~ ^
o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o'
lOMN't^S^^aiCD't^OlMnfOflOCOClCDCfO
OCiOOOOooNSNCOCDcDCOlOlOlClO^TfCQCOOlIN
о о' о' о' о' о' о' о' о' о о' о' о о' о' о' о' о' о' о' о' о
^Cibcp'tCN^C500biO'tCO(N^ONiOW^N^ 00501®CO)C)OOOOCDOOOOC£)OOOOOONNNbtnCD — OoOOOoOOOOOOOOOOOOOOO
o' o' Q o' q' о' о о о' о' о о' о о' о о о' о' о о о' о'
|
СП |
со |
|
СП |
см |
|
о |
со |
|
|
см" |
|
QO |
■'f |
|
СП |
ю |
|
о" |
Ол |
|
|
см' |
|
lo |
ю |
|
СП |
|
|
о“ |
со |
|
|
f—( |
|
g |
см
СО |
|
о |
см^ |
|
|
|
|
|
ю |
|
из |
г- |
|
t- |
со |
|
о' |
о" |
|
|
?• |
|
> |
3 |
go о ■ см
lOUjlOlOlOtbtDtO(D0NNNNSoOOO^O)^-H^
Стр. 12 ГОСТ 11.007-75
7.5. Определение верхней доверительной границы для параметра а при неизвестном значении параметра Ь и известном значении с осуществляется следующим образом:
задают одностороннюю доверительную вероятность у2 и вычисляют корни b и а уравнений (1) и (2) приложения 1;
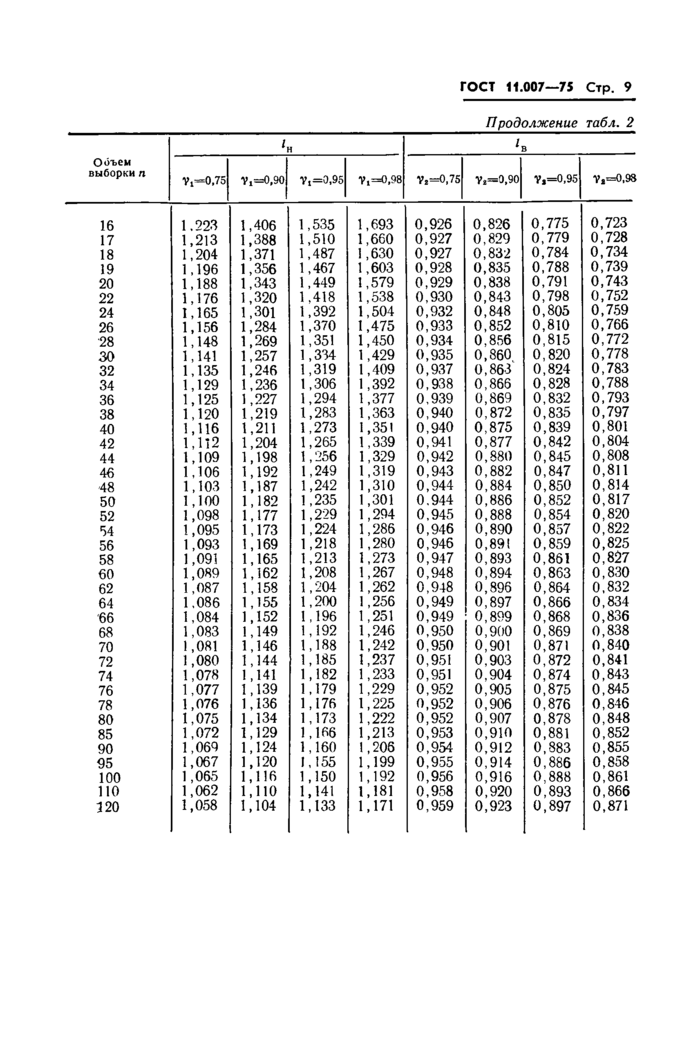
по заданному объему выборки п (5<п<120) и значению у2 из табл. 3 находят значение коэффициента zB;
определяют верхнюю доверительную границу для параметра а по формуле
при значении объема выборки п> 120 значение гв определяют по формуле
(21)
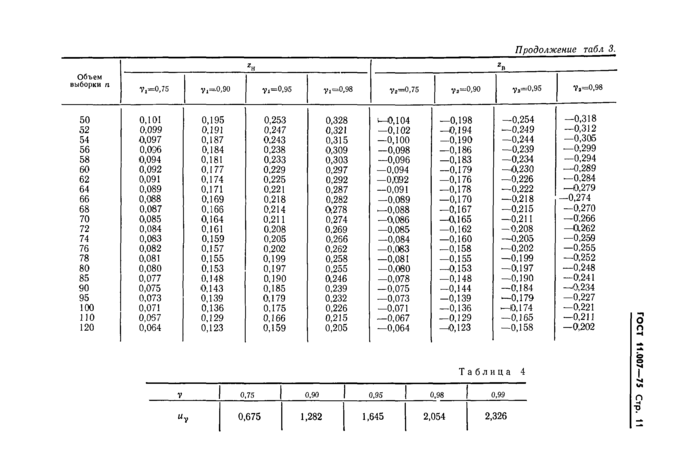
где Uy2 — приведено в табл. 4.
7.6. Определение доверительного интервала для параметра а при неизвестном значении параметра b и известном значении с осуществляют следующим образом:
задают доверительную вероятность у* и односторонние доверительные вероятности Уи и ?2 таким образом, чтобы у*, Yi и у2 удовлетворяли соотношению (13);
для односторонней доверительной вероятности у{ согласно п. 7.4 определяют нижнюю границу он;
для односторонней доверительной вероятности у2 согласно п. 7.5 определяют верхнюю доверительную границу ав;
нижняя ан и верхняя ав доверительные границы образуют доверительный интервал для параметра а при доверительной вероятности y* = Уь+Уг—1 (см. приложение 2, примеры 6, 8).
ПРИЛОЖЕНИЕ / Рекомендуемое
ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
1. Метод максимального правдоподобия применяется, когда имеются повышенные требования к эффективности оценок.
Случай [а, Ь]. Оценка параметров масштаба а и формы b при известном значении параметра сдвига с по методу максимального правдоподобия осуществляется путем решения системы уравнений
п
«2 (•*<—'c)b\n(xt—,с) п
JL— —----Ь2'п(^)=0> (1)
1 = 1
Решение уравнения (1) данного приложения осуществляется методом последовательных приближений (методом Ньютона — Рафсона) по рекуррентной формуле
S1=2 ln (-*«—c). (4)
(=1
4fe)=2(x~c) h ’ (5)
n A
^=2^-c) (6)
{=1
n /ч
S4fc)=2(Jf‘—b<i'ln2 (A—Ic).
i=1
Ьк — k~e приближение к корню b уравнения (1) данного приложения,
Ь0 — начальное приближение к корню b уравнения (1) данного приложения.
2. В качестве начального приближения может быть взято значение оценки Ь, полученной методом моментов, или значение оценки параметра 5, полученной с помощью вероятностных сеток (по ГОСТ 11.008-74), или значение оценки параметра Ь, полученной по значению вероятности Р0 с помощью табл. 1.
Я0=Вер{л:<Т}. (8)
Оценка вероятности Pq осуществляется по накопленной частости
(См. приложение 2, пример 8).
3. Чтобы получить несмещенную оценку b для параметра Ь, следует ум-
ножить значение корня b на коэффициент £(п), приведенный в таблице данного приложения.
Оценка а параметра а получается из уравнения (2) данного приложения,
в которое вместо значения b подставляется значение b (см. приложение 2, пример 6).
|
Значения В (п) для получения несмещенной оценки параметра формы b |
|
п |
В(п) |
п |
В(п) |
п |
В(п) |
п |
В(п) |
п |
В(п) |
|
5 |
0,669 |
15 |
0,908 |
3i |
0,960 |
54 |
0,975 |
74 |
0,982 |
|
6 |
0,752 |
16 |
0,914 |
36 |
0,962 |
56 |
0,976 |
76 |
0,983 |
|
7 |
0,792 |
18 |
0,923 |
38 |
0,964 |
58 |
0,977 |
78 |
0,983 |
|
8 |
0,820 |
20 |
0,931 |
40 |
0,968 |
60 |
0,978 |
80 |
9,984 |
|
9 |
0,842 |
22 |
0,938 |
42 |
0,968 |
62 |
0,979 |
85 |
9,985 |
|
10 |
0,859 |
24 |
0,943 |
41 |
0,970 |
64 |
0,980 |
90 |
0,985 |
|
11 |
0,872 |
26 |
0,947 |
46 |
0,971 |
66 |
0,98с |
1 100 |
0,987 |
|
12 |
0,883 |
28 |
0,951 |
48 |
0,972 |
68 |
0,981 |
120 |
0,990 |
|
13 |
0,893 |
30 |
0,955 |
50 |
0,973 |
70 |
0,981 |
|
|
|
14 |
0,901 |
32 |
0,958 |
52 |
0,974 |
72 |
0,982 |
|
|
|
4. Случай [а, с]. Оценка параметра а и с при известном значении параметра b~bQ по методу максимального правдоподобия осуществляется следующим образом:
— если значение \0<Ь0<2, то в качестве оценки параметра с берут минимальное значение хп(\) из наблюденных значений хи х3, . . хп;
— вычисляют оценку параметра а по формуле
(10)
(См. приложение 2, пример 9).
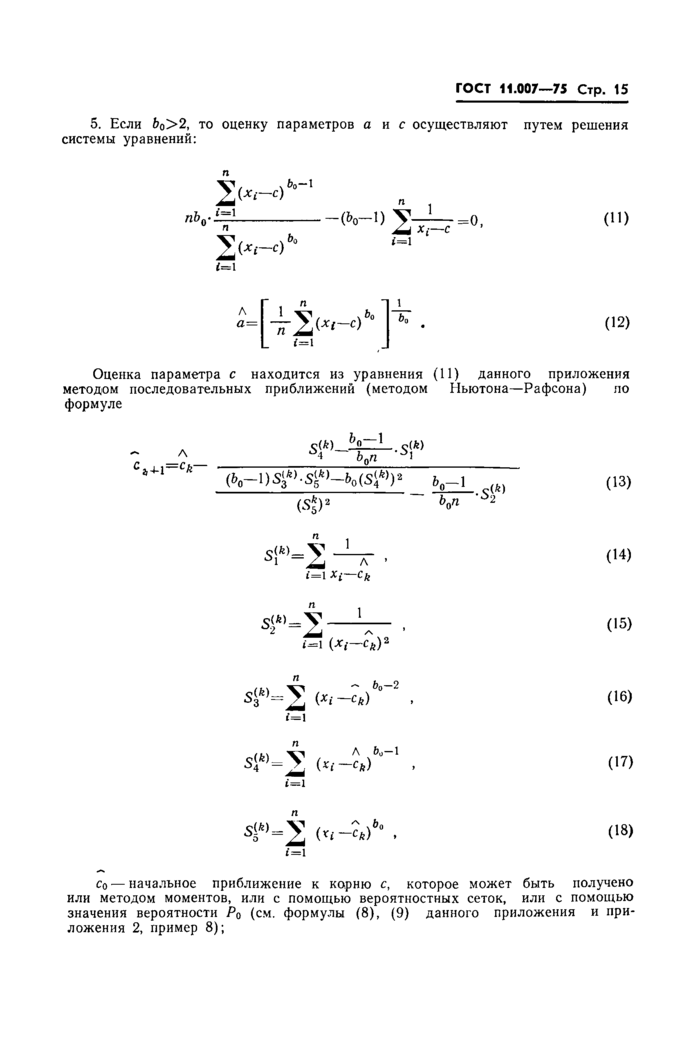
5. Если Ьо>2, то оценку параметров а и с осуществляют путем решения системы уравнений:
(12)
Оценка параметра с находится из уравнения (11) данного приложения методом последовательных приближений (методом Ньютона—Рафсона) по
формуле
(b0~l)S^-Slk)~b0(Sik>)2 b,
4^=2 ^~Ck)b° 2 - (16>
i=1
/L\ Ж’I A b0 1
si*>=2 (*<-<*) . (17>
t=l
si*>=2 (4-V". 08)
1=1
Co — начальное приближение к корню с, которое может быть получено или методом моментов, или с помощью вероятностных сеток, или с помощью значения вероятности Р0 (см. формулы (8), (9) данного приложения и приложения 2, пример 8);
по полученному значению с=с и данному значению Ь0 согласно формуле (12) данного приложения находят оценку для параметра а (см. приложение 2, пример 10).
6. Случай [а, Ь, с]. Оценка параметров а, b, с распределения Вейбулла по методу максимального правдоподобия осуществляется путем решения системы уравнений:
(20)
-2 <*->■
(21)
Решение системы уравнений (19), (20), (21), осуществляется следующим образом:
согласно п. 2 данного приложения находят начальное приближение для оценок параметров а, Ь, с.
Если окажется, что начальное приближение оценки параметра b не более 2, то в качестве оценки параметра сдвига берут наименьшее значение хп (1) из наблюденных значений хи х2, . . хп.
Затем из уравнения (20) методом последовательных приближений (методом Ньютона—Рафсона) находят оценку для параметра b по формулам (3)—(7) данного приложения, где вместо значения с следует подставлять значение хп (1) (см. приложение 2, пример 11).
ГОСТ 11.007—75 Стр. 17
ПРИЛОЖЕНИЕ 2 Справочное
ПРИМЕРЫ ПРИМЕНЕНИЯ ПРАВИЛ СТАНДАРТА
|
Таблица 1
Значения xt |
|
10,96 |
13,445 |
3,670 |
3,703 |
7,744 |
16,832 |
|
5,532 |
6,182 |
6,472 |
17,034 |
|
|
|
Пример 1. Дано 10 наблюдений случайной величины X, подчиняющейся распределению Вейбулла с известными значениями параметров формы Ь=2 и сдвига с—2. Найти оценку для параметра масштаба а. Результаты наблюдений приведены в табл. 1 данного приложения.
Решение. Согласно формуле (2) получают:
Г 10
Пример 2. Дано 100 наблюдений случайной величины, подчиняющейся распределению Вейбулла, если известно, что параметр сдвига с=0.
Результаты наблюдений, расположенные в порядке возрастания (вариационный ряд), приведены в табл. 2 данного приложения. Найти методом моментов оценки для параметров формы b и масштаба а.
|
Таблица 2
Значения х i |
|
0,027 |
0,251 |
0,446 |
0,667 |
0,843 |
|
0,033 |
0,266 |
0,480 |
0,670 |
0,855 |
|
0,091 |
0,267 |
0,506 |
0,675 |
0,887 |
|
0,106 |
0,270 |
0,510 |
0,705 |
0,925 |
|
0,117 |
0,273 |
0,561 |
0,706 |
0,937 |
|
0,135 |
0,288 |
0,576 |
0,738 |
0,949 |
|
0,136 |
0,291 |
0,588 |
0,741 |
0,949 |
|
0,211 |
0,333 |
0,611 |
0,748 |
0,986 |
|
0,211 |
0,342 |
0,615 |
0,748 |
0,987 |
|
0,228 |
0,363 |
0,631 |
0,749 |
1,085 |
|
0,231 |
0,415 |
0,646 |
0,778 |
1,127 |
|
0,236 |
0,434 |
0,646 |
0,782 |
1,161 |
|
0,239 |
0,445 |
0,649 |
0,826 |
1,198 |
|
|
Продолжение таблч 2 |
|
1,225 |
1,373 |
1,435 |
1,822 |
2,185 |
|
1,242 |
1,375 |
1,501 |
1,849 |
2,285 |
|
1,248 |
1,418 |
1,521 |
1,897 |
2,646 |
|
1,265 |
1,419 |
1,573 |
1,964 |
3,101 |
|
1,283 |
1,421 |
1,745 |
1,969 |
3,904 |
|
1,341 |
1,427 |
1,764 |
2,031 |
4,007 |
|
1,363 |
1,432 |
1,807 |
2,038 |
4,388 |
|
Решение. Согласно формулам (3), (4) и (5) вычисляют
1 100
-Tool *‘-=!'034,
i=1
Из табл. 1 находят, что для 6=1,10 v = 0,910, а для 6=1,20 vb =0,83?. Применяя линейную интерполяцию:
6Х — 1,10; vbl =0,910;
Ъ= ; оь=0,Ш;
Ъ2 — \ ,20; vb2 =0,837,
получают
. , Щ-Ьъг Vb2-bb 1,20(0,845-0 910) 1,10(0,837-0,845)
Vb2 —vbi +%&2 — vbl - 0,837—0,910 + 0,837—0,910
С помощью табл. 1 и используя линейную интерполяцию, получают значение кь;
6^1,10; Кьг =0,965;
6 = 1,19; Кь= ;
Ь2= 1,20; Кьг =0,940.
Согласно формуле (6) находят оценку для параметра масштаба а
1,034 а~0,942 ~1,10'
Таким образом оценки для параметров а и 6 следующие:
а= 1,10; 6=1,19.
УДК 658.562.012.71083.74J Группа Т59
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Прикладная статистика ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
Applied statistics. iPioint and interval estimators for parameters of weibull distribution
Постановлением Государственного комитета стандартов Совета Министров ССОР от 5 сентября 1975 г. № 2347 срок введения установлен
с 01.07. 1976 г.
Настоящий стандарт устанавливает правила определения оценок и доверительных границ для параметров распределения Вей-булла по совокупности статистических (опытных) данных, полученных на производстве в процессе измерений, испытаний и анализов, если эти опытные данные подчиняются распределению Вейбулла.
1. ОБЩИЕ ПОНЯТИЯ И ПОЛОЖЕНИЯ
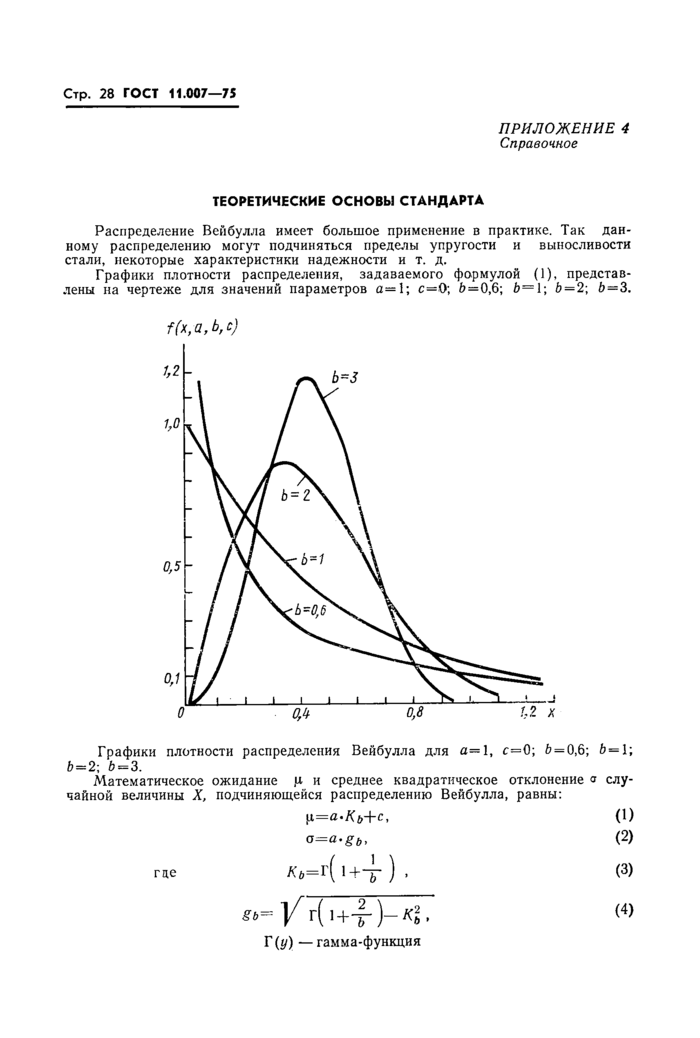
1.1. Правила и положения данного стандарта устанавливаются для распределения Вейбулла, задаваемого плотностью распределения:
/(*, а, Ь, с)= |— (—' “ , если х>с (1)
( 0, если x<ic,
где а — параметр масштаба, b — параметр формы, с — параметр сдвига (см. приложение 4, чертеж).
1.2. Оценка параметров а, Ь, с осуществляется по выборке независимых наблюдений хи х2, . . ., хп случайной величины
X, заведомо подчиняющейся распределению Вейбулла. Согласие наблюдений хи %2> • . хпс распределением Вейбулла — по
ГОСТ 11.006-74.
Переиздание. Ноябрь 1977 г.
ГОСТ 11.007-75 Стр. 19
Пример 3. табл. 2 примера 2 дано 100 наблюдений случайной величины X, подчиняющейся распределению Вейбулла. Известно, что 6 =1,2. Методом моментов найти оценки для параметров масштаба и сдвига.
Решение. Из табл. 1 определяют значение коэффициентов К ь и . В нашем случае для 6=1,20 имеем Кь —0,940; g*=0,787.
Определяют среднее значение х и среднее квадратическое отклонение 5
1 юо
1*034;
Согласно формуле (7) определяют оценку а для параметра а
- 0,874 ,
0,787 ~1,115*
По формуле (8) определяют
с=1,034—I,115-0,940=— 0,014.
Согласно формуле (9) в качестве оценки параметра сдвига с берут значение с = —0,014, так как
Г=-0,014<*1ОО(1)=0,027.
Таким образом оценки для параметров масштаба а и сдвига с следующие:
а= 1,115; Г=-0,014.
Пример 4. Для 100 наблюдений, приведенных в табл. 2 примера 2, найти методом моментов оценки для параметров масштаба, формы и сдвига распределения Вейбулла.
Решение. Согласно формуле (10) вычисляют:
100
99-98 х*~~ 1 > 034)3
i=\
~ | 100 “|3/2 gg-^(x(.-l,034)2 (=1
где х= 1,034; 5=0,874 получено согласно примеру 2.
По значению р* = 2,109 из табл. 1 находят значение 6 = 0,97; /(* = 1,013; ££ = 1,043. В данном случае применена линейная интерполяция для получения1 значений 6 = 0,97; /(* = 1,013; g*= 1,043.
Согласно п. 5.1 и формуле (7)) вычисляют:
л— 1,043 —°-838-
Стр. 2 ГОСТ 11.007-75
1.3. Стандарт устанавливает правила определения оценок для параметров а, б, с методом моментов для следующих случаев:
[а]—оценка параметра масштаба а при известном значении параметров формы б и сдвига с,
[а, б] —оценка параметров масштаба а и формы б при известном значении параметра сдвига с,
[а, с] —оценка параметров масштаба а и сдвига с при известном значении параметров формы б,
[а, б, с] —оценка всех трех параметров.
Стандарт устанавливает правила определения доверительных границ для параметров а, б, с для случаев:
[а] — определение доверительных границ для параметра а при известных значениях параметров формы б и сдвига с;
[а, б] —определение доверительных границ для параметров масштаба а и формы б при известном значении параметра сдвига с.
2. ОЦЕНКА ПАРАМЕТРА МАСШТАБА а ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРОВ ФОРМЫ b И СДВИГА с (СЛУЧАЙ [а]]
2.1. Оценка параметра а при известном значении параметров бис осуществляется по формуле
п \1_
s у
~\ /
(См. приложение 2, пример 1).
3. ОЦЕНКА ПАРАМЕТРОВ МАСШТАБА а И ФОРМЫ b ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРА СДВИГА с (СЛУЧАЙ [а, Ь])
3.1. Оценка параметров а и б при значении параметра с осуществляется следующим образом:
вычисляют выборочное среднее арифметическое значение х и выборочное среднее квадратическое отклонение 5 по формулам:
п
*=4*2**> (з)
t=\ t=l
ГОСТ 11.007-75 Стр. 3
а также отношение
= , (5)
X—С
по полученному значению vb из табл. 1 находят значение оценки Ь параметров Ь и значение коэффициента Къ\
по полученному значению Кь определяют оценку для параметра а по формуле
X—с
Кь
Если в табл. 1 нет соответствующего значения vb, то необходимо воспользоваться линейной интерполяцией (см. приложение 2, пример 2).
4. ОЦЕНКА ПАРАМЕТРОВ МАСШТАБА а И СДВИГА с ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРА ФОРМЫ Ъ (СЛУЧАИ [ат с])
4.1. Оценка параметров а и с при известном значении параметра b = b0 осуществляется следующим образам:
по значению параметра b = b0 из табл. 1 находят значение коэффициентов gb и Кь ;
определяют оценку для параметра а по формуле
- S
а=—
ёь
где S — определяется согласно формуле (4); находят значение с по формуле
с х аКь (3)
в качестве оценки параметра с берут одно из двух значений:
I с, если с<хл(1).
1лгл(1), еслис>л:/г(1), где х„(1)—наименьшее значение среди наблюденных значений
(См. приложение 2, пример 3).
5. ОЦЕНКА ПАРАМЕТРОВ МАСШТАБА а ФОРМЫ Ь И СДВИГА с {СЛУЧАЙ [а Ь.с])
5.1. Оценка параметра а осуществляется следующим образом: определяют асимметрию р4 по формуле
Стр. 4 ГОСТ 11.007-75
по полученному значению р6 из табл. 1 находят оценку Ь параметра b и значения коэффициентов gb и /С*;
по полученному значению b осуществляют оценку параметров. а и с согласно разд. 4.
(См. приложение 2, пример 4).
6. ПРАВИЛА ОПРЕДЕЛЕНИЯ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРА МАСШТАБА а ПРИ ИЗВЕСТНЫХ ЗНАЧЕНИЯХ ПАРАМЕТРОВ ФОРМЫ b И СДВИГА с (СЛУЧАЙ [а])
6.1. Определение доверительных границ для параметра а при известном значении параметров b и с сводится к определению доверительных границ для параметров экспоненциального распределения и осуществляется следующим образом:
из совокупности наблюдений хи х2, . . хп образуют
совокупность величин
Ух={Х —с)Ь> Уг = {Хъ—с)Ь,...,уп={Хп—с)Ь\
по совокупности значений уь уъ> • • •, у п согласно
ГОСТ 11.005-74 образуют доверительные границы для парамет-, 1
pa л = — экспоненциального распределения;
вычисляют нижнюю доверительную границу для параметра а по формуле
гдеХв— верхняя доверительная граница для параметра X, найденная согласно ГОСТ 11.005-74; вычисляют верхнюю доверительную границу для параметра а по формуле
где Ан— нижняя доверительная граница для параметра А, най-денная согласно ГОСТ 11.005-74;
ГОСТ 11.007'—75 Стр. 5
нижняя и верхняя доверительные границы ан, ав образуют доверительный интервал для параметра а, соответствующий доверительной вероятности у*
7*=Ti+T.-l. (13)
Ti>0.5; т2>0Д
где — односторонняя доверительная вероятность, соответствующая доверительной транице ан;
72 — односторонняя доверительная вероятность, соответствующая верхней доверительной границе ав.
Вер {л>лн) = т1; Вер {а\<ав}=т2.
(См. приложение 2, пример 5).
7. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ МАСШТАБА а И ФОРМЫ b ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРА СДВИГА с (СЛУЧАЙ [а, Ъ]).
7.1. Определение нижней доверительной границы b н для параметра b при неизвестном значении параметра а и известном значении параметра с осуществляется следующим образом: задают одностороннюю доверительную вероятность Уь
вычисляют корень Ь уравнения (1) приложения 1; по заданному объему выборки п (5</г<120) и заданному значению Vi в табл. 2 находят значение коэффициента /н;
вычисляют нижнюю доверительную границу для параметра Ь по формуле
при значении объема выборки /г> 120 значение коэффициента /н вычисляют по формуле
, 1 , 1 / 0,608
^н=1+ у (15)
где иУх — квантиль нормального распределения, соответствующая вероятности Yi (см. табл. 4).
7.2. Определение верхней доверительной границы Ьв для параметра b при неизвестном значении параметра а и известном значении параметра с осуществляется следующим образом: задают одностороннюю доверительную вероятность Уг;
вычисляют корень b уравнения (1) приложения 1; по заданному объему выборки п (5<п<120) и значению из табл. 2 находят значение коэффициента 1В\
Стр. 6 ГОСТ 11.007-75
вычисляют верхнюю доверительную границу для параметра Ь по формуле
б.-f ; (16)
LB
при значении объема выборки «>120 значение /в определяется по формуле
, , _ /0.608
г /г * ^V2 - (17)
где значение иУг —приведено в табл. 4 (см. п. 7.1). (См. приложение 2, примеры 6,7).
7.3. Определение доверительного интервала для параметра b при неизвестном значении параметра а и известном значении параметра с осуществляется следующим образом:
задают доверительную вероятность Y* и односторонние доверительные вероятности Yi и у2 таким образом, чтобы у*, yi и У% удовлетворяли соотношению (13);
для односторонней доверительной вероятности у \ согласно п. 7.1 определяют нижнюю доверительную границу Ьп\
для односторонней доверительной вероятности у2 согласно п. 7.2 определяют верхнюю доверительную границу Ьв;
нижняя Ьн и верхняя Ьв доверительной границы образуют доверительный интервал для параметра b с доверительной вероятностью
Т * = Т1+Т 2— 1 •
(См. приложение 2, примеры 6,7).
7.4. Определение нижней доверительной границы ан для параметра а при неизвестном значении параметра Ъ и известном значении с осуществляется следующим образом:
задают одностороннюю доверительную вероятность Уь
вычисляют корни b я а уравнений (1), (2) приложения 1; по заданному объему выборки « (5<«<120) и значению yt из табл. 3 находят значение коэффициента гн;
вычисляют нижнюю доверительную границу для параметра а по формуле
л
Л ~ZJb * V
а^а-е ; (18)
при значении объема выборки «>120 значение гн вычисляют по формуле
/1 108" п ’
где значение иУх —приведено в табл. 4 (см. п. 7.1).
ГОСТ 11.007-75 Стр. 7
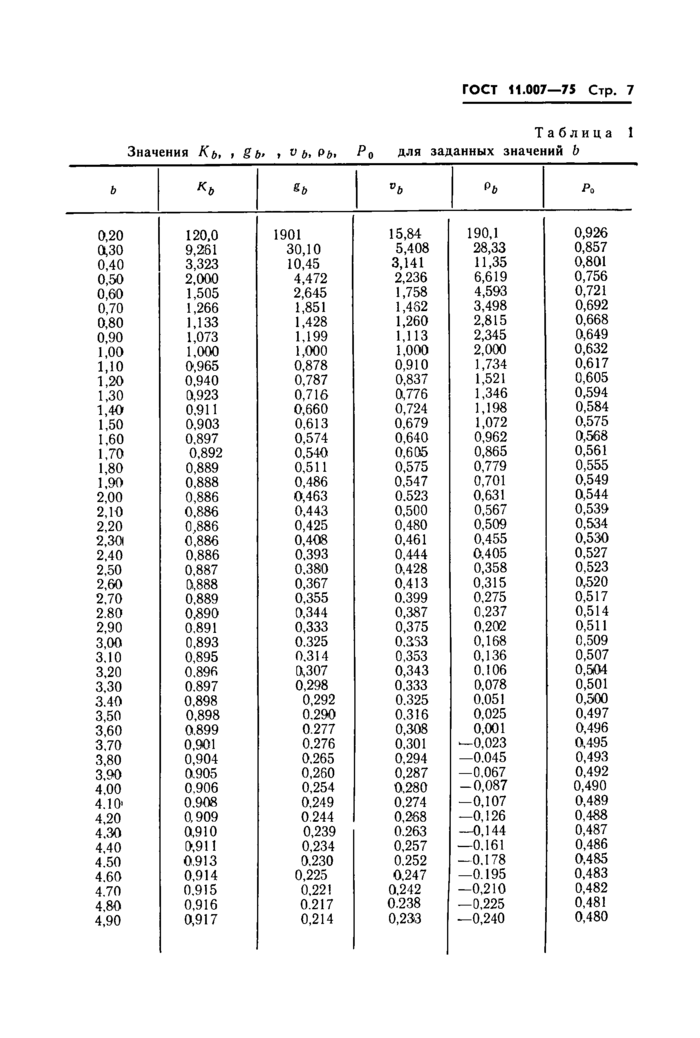
|
Таблица 1
Значения Кь* г 8Ь> » v Ы Рг>» ?о для заданных значений b |
|
ъ |
К* |
Ч |
vb |
<>ь |
Ро |
|
0,20 |
120,0 |
1901 |
15,84 |
190,1 |
0,926 |
|
0,30 |
9,261 |
30Л0 |
5,408 |
28,33 |
0,857 |
|
0,40 |
3,323 |
10,45 |
3,141 |
11,35 |
0,801 |
|
0,50 |
2,000 |
4,472 |
2,236 |
6,619 |
0,756 |
|
0,60 |
1,505 |
2,645 |
1,758 |
4,593 |
0,721 |
|
0,70 |
1,266 |
1,851 |
1,462 |
3,498 |
0,692 |
|
0,80 |
1,133 |
1,428 |
1,260 |
2,815 |
0,668 |
|
0,90 |
1,073 |
1,199 |
1,113 |
2,345 |
0,649 |
|
1,00 |
1,000 |
1,000 |
1,000 |
2,000 |
0,632 |
|
1,10 |
0,965 |
0,878 |
0,910 |
1,734 |
0,617 |
|
1,20 |
0,940 |
0,787 |
0,837 |
1,521 |
0,605 |
|
1,30 |
0,923 |
0,716 |
0,776 |
1,346 |
0,594 |
|
1,40 |
0,911 |
0,660 |
0,724 |
1,198 |
0,584 |
|
1,50 |
0,903 |
0,613 |
0,679 |
1,072 |
0,575 |
|
1,60 |
0,897 |
0,574 |
0,640 |
0,962 |
0,568 |
|
1,70 |
0,892 |
0,540 |
0,606 |
0,865 |
0,561 |
|
1,80 |
0,889 |
0,511 |
0,575 |
0,779 |
0,555 |
|
1,90 |
0,888 |
0,486 |
0,547 |
0,701 |
0,549 |
|
2,00 |
0,886 |
0,463 |
0.523 |
0,631 |
0,544 |
|
2,10 |
0,886 |
0,443 |
0,500 |
0,567 |
0,539 |
|
2,20 |
0,886 |
0,425 |
0,480 |
0,509 |
0,534 |
|
2,30 |
0,886 |
0,408 |
0,461 |
0,455 |
0,530 |
|
2,40 |
0,886 |
0,393 |
0,444 |
0,405 |
0,527 |
|
2,50 |
0,887 |
0,380 |
0,428 |
0,358 |
0,523 |
|
2,60 |
0,888 |
0,367 |
0,413 |
0,315 |
0,520 |
|
2,70 |
0,889 |
0,355 |
0,399 |
0,275 |
0,517 |
|
2.80 |
0,890 |
0,344 |
0,387 |
0,237 |
0,514 |
|
2,90 |
0,891 |
0,333 |
0,375 |
0,202 |
0,511 |
|
3,00 |
0,893 |
0,325 |
0,353 |
0,168 |
0,509 |
|
ЗЛО |
0,895 |
0.314 |
0,353 |
0,136 |
0,507 |
|
3,20 |
0,896 |
0,307 |
0,343 |
0,106 |
0,504 |
|
3,30 |
0.897 |
0,298 |
0,333 |
0,078 |
0,501 |
|
3,40 |
0,898 |
0,292 |
0.325 |
0,051 |
0,500 |
|
3,50 |
0,898 |
0,290 |
0,316 |
0,025 |
0,497 |
|
3,60 |
0,899 |
0.277 |
0,308 |
0,001 |
0,496 |
|
3,70 |
0,901 |
0,276 |
0,301 |
—0,023 |
0,495 |
|
3,80 |
0,904 |
0.265 |
0,294 |
—0,045 |
0,493 |
|
3,90 |
0.905 |
0,260 |
0,287 |
—0,067 |
0,492 |
|
4,00 |
0,906 |
0,254 |
0,280 |
-0,087 |
0,490 |
|
4.10' |
0.908 |
0,249 |
0,274 |
-0,107 |
0,489 |
|
4,20 |
0,909 |
0.244 |
0,268 |
—0,126 |
0,488 |
|
4,30 |
0,910 |
0,239 |
0.263 |
—0,144 |
0,487 |
|
4,40 |
0,911 |
0,234 |
0,257 |
—0,161 |
0,486 |
|
4.50 |
0.913 |
0,230 |
0,252 |
—0,178 |
0,485 |
|
4,60 |
0,914 |
0,225 |
0.247 |
—0.195 |
0,483 |
|
4.70 |
0,915 |
0,221 |
0,242 |
—0,210 |
0,482 |
|
4,80 |
0,916 |
0.217 |
0.238 |
—0,225 |
0,481 |
|
4,90 |
0,917 |
0,214 |
0,233 |
—0,240 |
0,480 |
|
|
Продолжение табл. 1 |
|
ъ |
*6 |
|
vb |
р * |
Ро |
|
5,00 |
0,918 |
0,210 |
0,229 |
■—0,254 |
0,479 |
|
5,Ю |
0,919 |
0,207 |
0,225 |
—0,268 |
0,478 |
|
5,20 |
0,920 |
0,203 |
0,221 |
—0,281 |
0,477 |
|
6,30 |
0,921 |
0,199 |
0,217 |
■—0,294 |
0,477 |
|
5,40 |
0,922 |
0,197 |
0,213 |
—0,306 |
0,476 |
|
5,50 |
0,923 |
0,194 |
0,210 |
—0,318 |
0,475 |
|
5,60 |
0,924 |
0,190 |
0,206 |
—0,330 |
0,474 |
|
5,70 |
0,925 |
0,187 |
0,203 |
—0,341 |
0,474 |
|
5,80 |
0,926 |
0,184 |
0,200 |
—0,352 |
0,473 |
|
5,90 |
0,927 |
0,181 |
0,197 |
—0,363 |
0,472 |
|
6,00 |
0,928 |
0,180 |
0,194 |
—0,373 |
0,471 |
|
6,10 |
0,928 |
0,177 |
0,191 |
—0,383 |
0,471 |
|
6,20 |
0,929 |
0,175 |
0,188 |
—0,393 |
0,471 |
|
6,30 |
0,930 |
0,173 |
0,185 |
—0.403 |
0,470 |
|
6,40 |
0,931 |
0,170 |
0,183 |
|—0,412 |
0,469 |
|
6,50 |
0,932 |
0,168 |
0,180 |
—0,421 |
0,468 |
|
6,60 |
0,932 |
0,166 |
0,177 |
—0,430 |
0,468 |
|
6,70 |
0,933 |
0,163 |
0,175 |
—0,439 |
0,468 |
|
6,80 |
0,934 |
0,161 |
0,173 |
—0,447 |
0,467 |
|
6,90 |
0,935 |
0,159 |
0,170 |
—0,455 |
)0i468 |
|
7,00 |
0,935 |
0,157 |
0,168 |
—0,463 |
0,465 |
|
7,50 |
0,939 |
0,147 |
0,158 |
—0,500 |
0,464 |
|
8,00 |
0,942 |
0,140 |
0,148 |
—0,534 |
0,461 |
|
8,50 |
0,945 |
0,131 |
0,140 |
—0,564 |
0,460 |
|
9,00 |
0,947 |
0,126 |
0,133 |
—0,591 |
0,458 |
|
9,50 |
0,949 |
0,120 |
0,126 |
—0,615 |
0,457 |
|
10,00 |
(0,951 |
0,114 |
0,120 |
—0,638 |
0,455 |
|
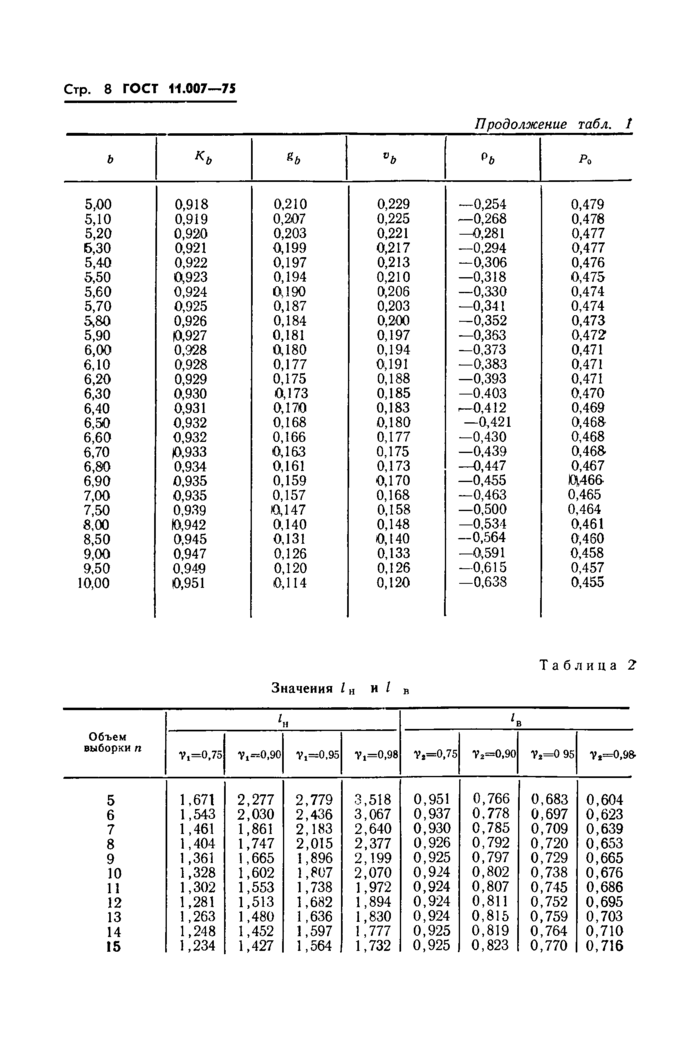
|
Таблица 2
Значения / н и / в |
|
Объем выборки п |
|
1 |
н |
|
|
|
|
|
|
Vi=0,75 |
Vi=0,90 |
71=0,95 |
71=0,98 |
72=0,75 |
V 2=0.90 |
?2=0 95 |
7*=0,9& |
|
5 |
1,671 |
2,277 |
2,779 |
3,518 |
0,951 |
0,766 |
0,683 |
0,604 |
|
6 |
1,543 |
2,030 |
2,436 |
3,067 |
0,937 |
0,778 |
0,697 |
0,623 |
|
7 |
1,461 |
1,861 |
2,183 |
2,640 |
0,930 |
0,785 |
0,709 |
0,639 |
|
8 |
1,404 |
1,747 |
2,015 |
2,377 |
0,926 |
0,792 |
0,720 |
0,653 |
|
9 |
1,361 |
1,665 |
1,896 |
2,199 |
0,925 |
0,797 |
0,729 |
0,665 |
|
10 |
1,328 |
1,602 |
1,807 |
2,070 |
0,924 |
0,802 |
0,738 |
0,676 |
|
11 |
1,302 |
1,553 |
1,738 |
1,972 |
0,924 |
0,807 |
0,745 |
0,686 |
|
12 |
1,281 |
1,513 |
1,682 |
1,894 |
0,924 |
0,811 |
0,752 |
0,695 |
|
13 |
1,263 |
1,480 |
1,636 |
1,830 |
0,924 |
0,815 |
0,759 |
0,703 |
|
14 |
1,248 |
1,452 |
1,597 |
1,777 |
0,925 |
0,819 |
0,764 |
0,710 |
|
15 |
1,234 |
1,427 |
1,564 |
1,732 |
0,925 |
0,823 |
0,770 |
0,716 |
|