МИНИСТЕРСТВО НЕФТЯНОЙ ПРОМЫШЛЕННОСТИ

ВНИИСПТнефть

РУКОВОДЯЩИЙ ДОКУМЕНТ

МЕТОДИЧЕСКОЕ РУКОВОДСТВО ПО ОБОСНОВАНИЮ И ВЫБОРУ МОДЕЛЕЙ ПРИ ГИДРАВЛИЧЕСКИХ И ТЕПЛОВЫХ РАСЧЕТАХ

ТРУБОПРОВОДОВ РД 39-30-857-83

1984

Министерство нефтяной промышленности

ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ПО СВОРУ, ПОДГОТОВКЕ И ТРАНСПОРТУ НЕФТИ И НЕФТЕПРОДУКТОВ

(ВНИИСПТнефть)

утверждено

первый заместителем министра нефтяной промышленности В.И.Игревским 12 января 1983г.

РУКОВОДЯЩИЙ ДОКУМЕНТ

МЕТОДИЧЕСКОЕ РУКОВОДСТВО ПО ОБОСНОВАНИЮ И ВЫБОРУ МОДЕЛЕЙ

ПРИ ГИДРАВЛИЧЕСКИХ и тепловых расчетах ТРУБОПРОВОДОВ

РД 39-30-857-83

1984

II

б) Для проведения распознавания или экзамена выбирается, на-пример, I -й эксперимент. Признаки этого эксперимента

IgA- -1,502; LgHe- 5,487; 1дйеш 4,210, вычисленные нормировочные коэффициенты (п.а) и коэффициенты 0(

(в.2) подставляются в (2.1) и (2.2).

Если распознавание проводится на уровне точности 0,01. то вычисление показателей экспонент в (2.1), (2.2) следует проводить е точностью до 0,01, так как дальнейоие уточнения не сказываются на результатах вычисления потенциальных функций с точностью до

0M(e*p(-CtOOj/x exp(-0,0*) = 0,99).

Для распознавания выбранного (1-го) эксперимента знамения потенциальных функций подучились следующими:

К^Тш 2,96;    Д^с-    2,92    .

Здесь /Т^Г> /Т^С .Следовательно, выбранный (I-Й) эксперимент

С

относится к турбулентной области течения. В результате экзамена по оставшимся 33 экспериментам (соответственно 16 из области турбулентного течения и 17 из структурной области) правильно распознались 28 экспериментов, что составляет 86 % распознавания (100 % для турбулентной области и 75 % для структурной (табл. 3).

Пример 2.2

Применим метод потенциальных функций для диагностирования коэффициента гидравлического сопротивления трубопроводов, по которым транспортируется газонефтяная смесь на основе данных работы [_13] . В качестве потенциальной функции а данном примере взята зависимость вида

-llfi+crfffx. у)),    ₍₂.з,

-А.    /К*.у).    ft -yj '

Л - число параметров, характеризующих данный объект;

<Х-С0Л$1 >0 .

12

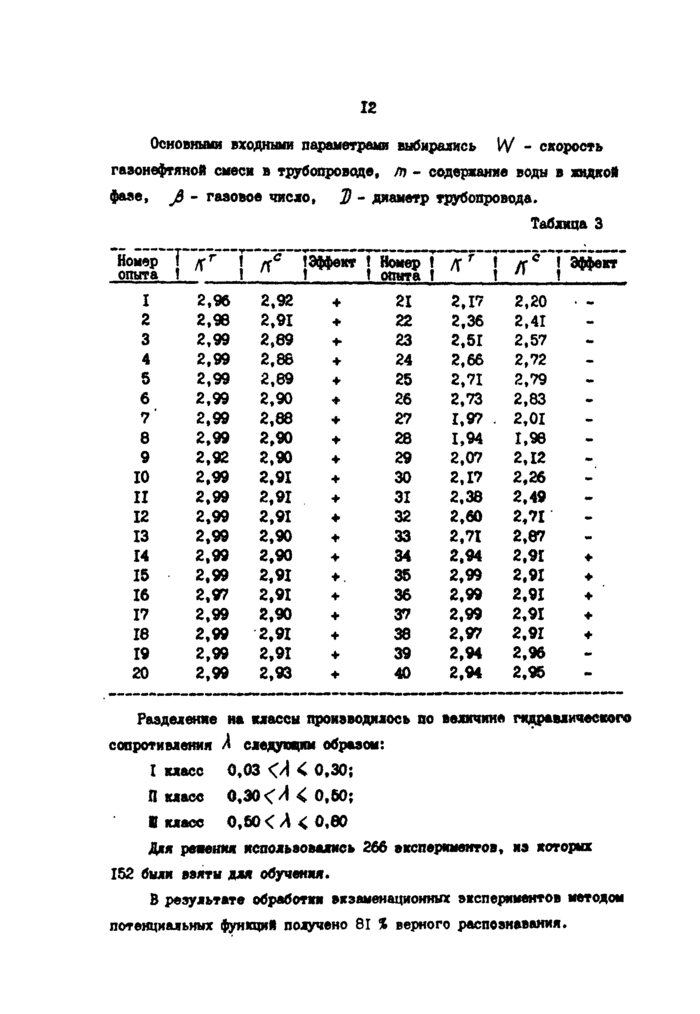
Основнши входными параметрами выбирались IV - скорость газонефтяной смеси в трубопроводе, т - содержание воды в ходкой фазе, j5 - газовое число, ]} - диаметр трубопровода.

Таблица 3

Разделение на классы производилось по величине гидравлического сопротивления Л сведущим образом:

I класс 0,03    <    0,30;

П класс 0,30 < Л < 0,60;

В класс 0,60 < Л < 0,0О

Для решения использовались 266 вкспериментов, из которых 152 были взяты для обучения.

В результате обработки вхзаменационных экспериментов методом потенциальных функций получено BI * верного распознавания.

13

2.2. Метод главных компонент

При выявлении характерных областей режимов течения важно проводить диагностирование по возможности по меньшему числу зависимых признаков. Это может быть достигнуто применением одного из методов распознавания образов - метода главных компонент.

Главные компоненты - это линейные комбинации статистических величин, характеризующиеся тем, что их нормированные линейные комбинации располагаются в порядке убывания дисперсии.

Метод главных компонент заключается в таком линейном преобразовании п случайных величин Х_у|..., в новый набор случайных величин Z_i ....»    * который сделал бы их независимыми и располо

жил в порядке убывания дисперсии. Число главных компонент равно числу признаков, однако несколько первых главных компонент учитывают всю долю изменения f3j .

Пример 2.3.

В примере 2.1 была показана возможность диагностирования характерных областей течения по параметрам А , Не % Re • Дм уменьшения числа зависимых признаков можно использовать метод главных компонент. Для этого строятся главные компоненты по параметрам:

I) A_fHe,Rt ;    2) А,Ие ; 3) A, Re ; 4) Ms, Re .

Ни», приводится полная схема построения главных компонент.

Имеется 40 наблюдший (табл. 2): N - 40, /7 -/К -1-39. Каждое наблюдение состоит из 3 измерений ( А , Не , Re ).

В результате вычислений по данным табл. 2 подучается следующей ковариационная матрица:

-0,1111

0,0045

0,1024

Для нахождения первой главной компоненты применяем метод последовательных приближений, вычисляя последовательно произведение

15

-W

выбирается начальное приближение Z и, аналогично, последовательно находятся Гг и    собственный    вектор второй главной

*

компоненты:

-0,3915

0,9847

-0,4334

Ее дисперсией будет

1_г ш у 0,0481²+0,0131²+0,0068² - 0,0506 . '

Вычисляется матрица    _а(г)_а(2)'

Находятся и    собственный вектор третьей главной компоненты:

/ -0,0096

O.OIbo \ 0,2361

0,0301²+0,0181²+0,0101² - 0,0134 . Результаты расчетов представляются в виде L- (0,5289, 0,0506, 0,0134) ;

0,7631    -0,3915    -0,0096

В «г    I 0,5845    0,9847    0,0185

.-0,2757    -0,4334    0,2361

• Следует отметить,, что на долю ^:первой главной компоненты при-

в

ходится 89 % общей дисперсии этих трех измерений. На долю второй компоненты - 9 % и третьей - 2 %. Общая дисперсия есть диагональный элемент ковариационной матрицы. Она равна сумме дисперсий главных компонент:

0,2601+0,2304+0,1024 - 0,5289+0,0506+0,0134 * 0,5929 . Графическая интерпретация результатов наблюдений в системе координат Z₄ и 2_г для главных компонент Л _f Hi , Яб приведена на рис. I. Значения Z_i и Z_£ вычисляются по уравнениям Z,- 0,7631 IgA +0,5845 l#Hejb,zmLgfa ;

Z_t - -0,3915 IgA +о,9в47-0,4334 Lgfe .

16

По параметрам А , ff$ процент ошибки составил 18 % для структурной области и 6 % для турбулентной области, по А * Нс -18 % и 6 %, по //* ,/?£ - 6 % и 35 соответственно.

Рис, I. Графическая интерпретация метода главных компонент

Пример 2.4

Как было показано выве, определяющую роль при диагностировании режимов течения играет коэффициент гидравлического сопротивления А - В связи с этим представляет интерес прогнозирование А при течении неньютоновских систем типа суспензий. При движении суспензий на J влияют такие факторы,как скорость, концентрация твердой фазы, вязкость, плотность суспензии. Для прогнозирования коэффициента гидравлического сопротивления можно использовать метод главных компонент.

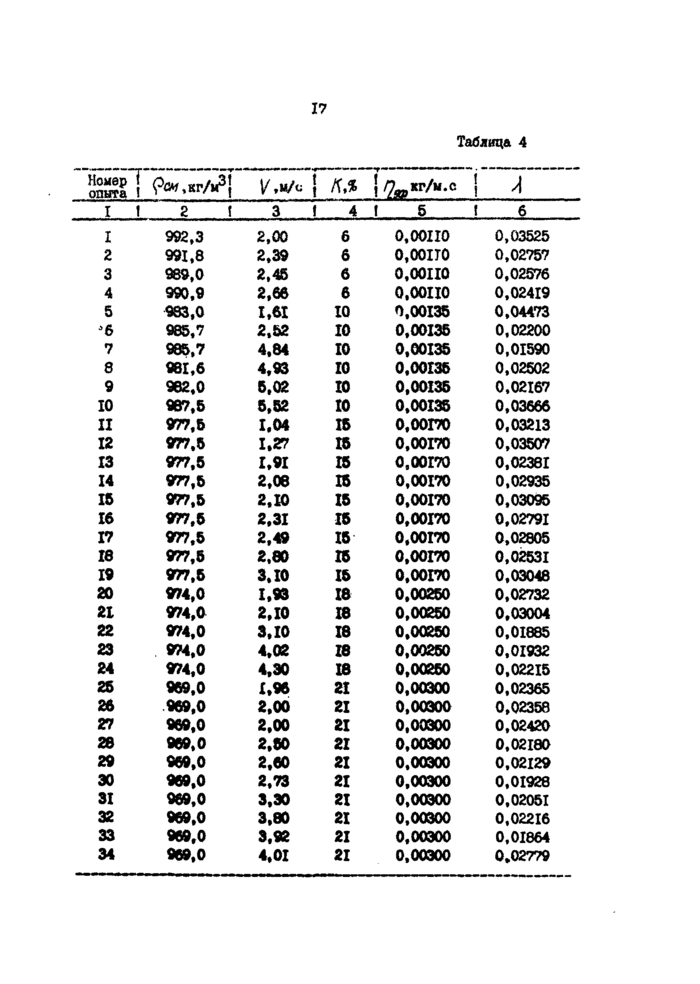
В качестве исходных данных были использованы результаты экспериментальных исследований со движению суспензий различной концентрацией твердой фазы. В качестве рабочих сред использовались водонесущая среда и гранулированные частицы полиэтилена с концентрацией от 6 до 34 %. Результаты экспериментов приведены в табл. 4.

б

0,02830

0,01701

0,03371.

0,02538

0,02202

0,01940

0,01697

0,01740

0,02114

0,02129

0,02073

о;озоз8

0,02522

0,02308

0,02747

0,03335

0,01902

0,02051

0,02735

0,01956

0,05449

0,03907

0,04079

0,02665

0,03041

0,03020

0,02375

0,02522

0,02182

0,02193

0,02462

0,02136

0,0X601

0,02136

0,01738

0,02378

19

I ! 2 ! 3 1 4 ! 5 ! 6 72 953,0 0,89 29 0,00510 0,03131 73 953,0 1,34 29 0,00510 0,03305 74 953,0 3,06 29 0,00510 0,0198© 75 953,0 3,11 29 0,00510 0,02051 76 953,0 3,53 29 0,00510 0,01990 77 953,0 3,93 29 0,00510 0,01846 78 953,0 4,03 29 0,00510 0,02215 79 953,0 4,34 29 0,00510 0,01712 80 953,0 4,67 29 0,00510 0,03130 81 953,0 4,88 29 0,00510 0,02885 82 953,0 5,41 29 0,00510 0,02883 83 949,0 1,33 31 0,00580 0,03277 84 949,0 1,42 31 0,00580 0,02831 85 949,0 1,94 31 0,00580 0,02968 86 949,0 3,98 ЗГ 0,00580 0,01620 87 947,0 4,83 34 0,00650 0,02766 88 947,0 5,45 34 0,00650 0,02206 89 947,0 5,54 34 0,00650 0,01827

Исследуемый объект характеризуется вектором состояния

<з

где р - плотность суспензии, кг/м ;

У ~ скорость потока, м/сек;

А

/Г - концентрация твердой фазы;

~ коэффициент гидравлического сопротивления;

- эффективная вязкость суспензии, кг/м.сек*

Пересчет исходной информации в компоненты Z, и проиэво дится по формулам:

(2.4>

J7 - -0,046^(0+0,188 IgV +0,631^-0,099^ +0,745^

Методическое руководство разработано Всесоюзным научно-исследовательским институтом по сбору, подготовке и транспорту нефти и нефтепродуктов (ВЙИИСПТнефть) под научным руководством академика АН АзССР А. X.Мирзаджанзаде.

Авторский коллектив: Галлямов А.К., Сковородников Ю.А., Саттаров Р.М., Юфян В.А., Мукук К.В., Мамедов А.В., Бахтизин Р.Н., Ризванов Н.Р., Хайбуллин Р.Я., Шамнаэов А.М., Бахииев А.А», Пивоваров В.1\, Васильченко С.В., Фаттахов М.М., Пирвердян Н.А.,

Настоящее руководство посвящено разработке методов контроля и регулирования работы трубопроводов, представляющих собой сложные системы. Рассмотрены вопросы расчета трубопроводов, транспортирующих различные гетерогенные системы (суспензии нефти, нефтепесчаные смеси, нефть с включениями парафина, газожидкостные потоки и др.) с учетом проявления неньютоновских свойств - реологических и гидродинамических параметров транспортируемых сред.

В методике подробно изложены вопросы обоснования и выбора моделей при гидравлических и тепловых расчетах трубопроводов с учетом адаптационных методов классификации и распознавания объектов на основе самоорганизующихся моделей.

Приведены методы диагностирования реологических свойств вязкоупругих нефтей при их движении по трубам.

Методическое руководство предназначено для инженерно-технических работников предприятий нефтяной промышленности, научно-исследовательских институтов и лабораторий, а также для студентов нефтяных вузов.

20

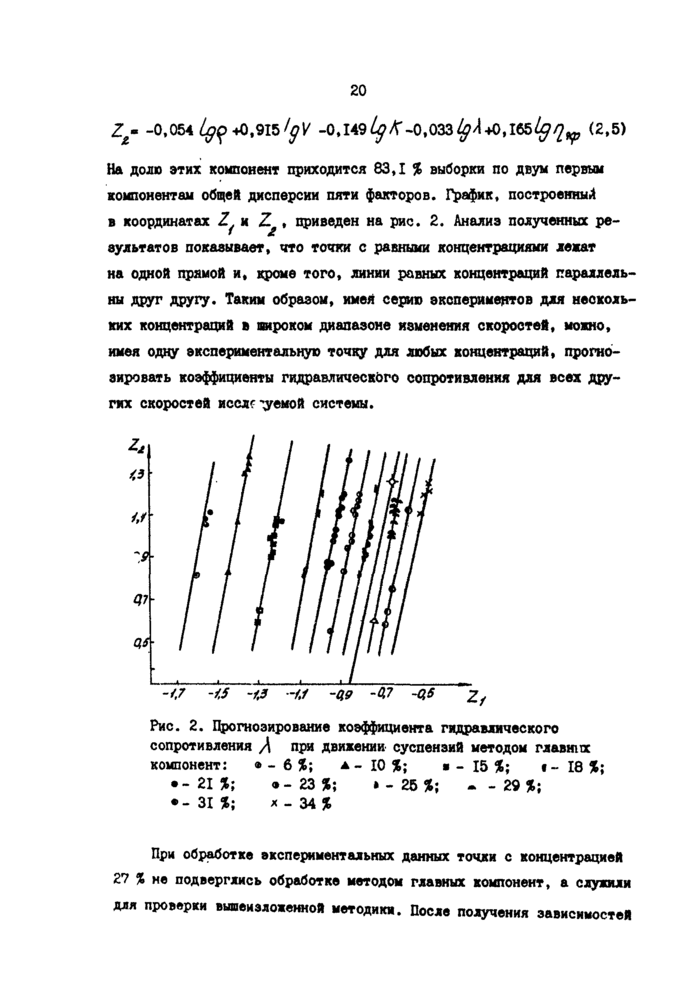
Z« -0,054    40,915    fgV    -О.МЭ^/Г-О.ОЗЗ^Л+Мбб^^ (2,5)

На долю этих компонент приходится 83,1 % выборки по двум первым компонентам общей дисперсии пяти факторов. График, построенный в координатах и Z_£, приведен на рис. 2. Анализ полученных результатов показывает, что точки с равными концентрациями лежат на одной прямой и, кроме того, линии равных концентраций параллельны друг другу. Таким образом, имея серию экспериментов для нескольких концентраций в широком диапазоне изменения скоростей, можно, имея одну экспериментальную точку для любых концентраций, прогнозировать коэффициенты гидравлического сопротивления для всех других скоростей исследуемой системы.

Рис. 2. Прогнозирование коэффициента гидравлического сопротивления /\ при движении суспензий методом главных компонент:    ®    -    6    56;    а    -    Ю    56;    ■    -    15    56;    t    -    18    56; • -21%;    <*    -    23    %;    »    -    25 56;    *    -    29    %; •- 31 56; х - 34 56

При обработке экспериментальных данных точки с концентрацией 27 % не подверглись обработке методом главных компонент, а служили для проверки вышеизложенной методики. После получения зависимостей

РУКОВОДЯЩИЙ ДОКУМЕНТ

Методическое руководство по обоснованию и выбору моделей при гидравлических и тепловых расчетах трубопроводов, РД 39-30-857-83

Вводится впервые

Приказом Министерства нефтяной промышленности от 01,06.83г. № 284 срок введения установлен с 01.06.83г.,

срок действия до 01.06.88 г.

I. ОПРЕДЕЛЕНИЕ СТЕПЕНИ ЗНАЧИМОСТИ ФАКТОРОВ, ВЛИЯЮЩИХ НА ИССЛЕДУЕМЫЙ ПРОЦЕСС

Расчет трубопроводов, транспортирующих различные гетерогенные системы (нефть с включениями парафина, суспензии нефти, нефтепесчаные смеси, газожидкостные потоки и др.), необходимо проводить с учетом проявления вышеуказанными средами неныотоновских свойств. Поэтому в зависимости от особенностей проявления реологических свойств таких систем пользуются обычно при гидравлических расчетах эмпирическими полузмпирическиии формулами, учитывающими те или иные гидродинамические и реологические параметры транспортируемых сред. При таком подходе следует расположить факторы, влияющие на процесс, по степени их влияния на гидравлические характеристики. Это необходимо как для выявления режима течения, так и для выбора аппроксимационной зависимости коэффициента гидравлического сопротивления.

В случае вязкопластичных сред на коэффициент гидравлического сопротивления влияют такие параметры как V , d , р , перекачиваемых по трубопроводам жидкостей.

Ниже приводится пример расчета информативности этих параметров на коэффициент гидравлического сопротивления на основании имею-

4

щейся экспериментальной информации при течении парафинистых нефтей в трубах.

Пример I.I.

По имеющимся экспериментальным исследованиям определялась информативность параметров V , d , <р , q , с точки зренйя влияния их на А по мере фгльбака flj . В качестве примера ниже приводится расчет информативности скорости течения неньютоновской системы в смысле влияния на А ₉ В основу обработки взяты 44 эксперимента, характеризующие различные режимы.

Все объекты (44 эксперимента) разбиваются на две группы А я В ^: первая характеризуется изменением коэффициента гидравлического сопротивления в диапазоне 0,0125 < А 4    0,0359; вто

рая - 0,0370 4^4 0,1680. Параметр V изменяется в диапазоне 1,02 м/с 4 V 4    6,11 м/с. Разобьем данный ряд на 8 интервалов

i

(табл. I) от 1,02 до 1,65, от 1,65 до 2,29 и т.д. (рекомендуется разбивать на 8-10 интервалов). Эти интервалы вносятся в таблицу I (графа 2). Следующие две графы (3 и 4) содержат данные по частоте попадания экспериментов из групп А и В в каждый интервал. Графы 5 и 6 заполняются значениями относительных частостей в процентах, принимая за 100% сумму частостей соответственно А и В во всех диапазонах. Например, для интервала 1,020*1,655 для группы А имеем (1:25)хЮ0»4. Чтобы свести к минимуму влияние выбора границ интервалов на результаты, в каддом интервале определяются средне-взвешенные (сглаженные) частости методом вычисления взвешенной скользящей средней. При этом учитываются частости данного признака У в четырех соседних диапазонах. Вычисление взвешенной скользящей средней производится по формуле

Чтобы подсчитать сглаженную частость в первом интервале_fвводятся некоторые фиктивные интервалы - нулевой и минус первый. По-

5

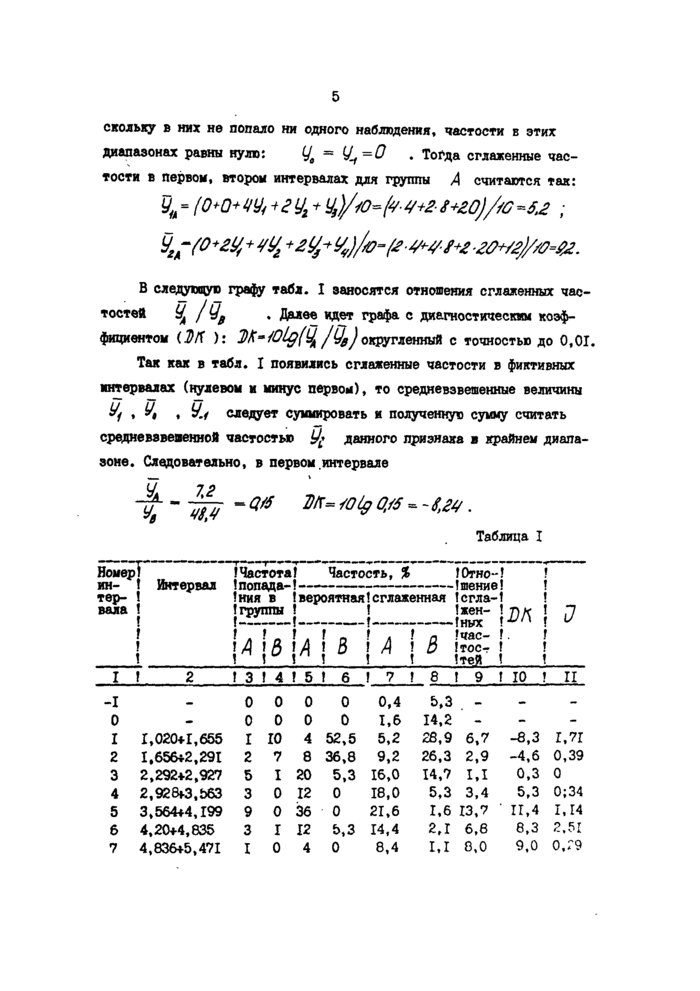
скольку в них не попало ни одного наблюдения, частости в этих диапазонах равны нулю:    У₀    =    У^—0    .    Тогда    сглаженные    час

тости в первом, втором интервалах для группы А считаются так:

У_и = (0+0+Щ +2У_г + y₃}/t0=(4-4+2 S+Z0)/fC~S,2 ; У_г-(0+гЦ+Щ +&Ц+у,)/0“(е-4+м+£ -2&+/2}/а°&.

В следующую графу табл. I заносятся отношения сглаженных частостей У_А /    * Далее идет графа с диагностическим коэф

фициентом т ): Ш^т Ю1д(У_А /Qg) округленный с точностью до 0,01.

Таблица I

Так как в табл. I появились сглаженные частости в фиктивных интервалах (нулевом и минус первом), то средневзвешенные величины У( % Уй * У.1 следует суммировать и полученную сумму считать средневзвешенной частостью данного признака в Крайнев диапазоне. Следовательно, в первом .интервале

!Частота!    Частость, % !0тно~!

ин- ' ! Интервал !попада-!-------------------!шение!

д

тер- !    !ния в !вероятная!сглаженная !сгла-!

вала !    !группы    !    !    !жен-    ! л*

!    !------!--------!----------!ных    !^^А

t    f д ? о    »    -    !    _п    f    л    ?    п    'час-    Г.

|    \А\д\А    \    В    \А    I    В

I	! 2	! 3	> 4	? 5	! 6	! 7	! 8 !	1 9	! 10 !	II
-I		0	0	0	0	0,4	5,3		—	—
0	-	0	0	0	0	1,6	14,2	-	-	-
I	1,020*1,655	I	10	4	52,5	5,2	28,9	6,7	-8,3	1,71
2	1,656*2,291	2	7	б	36,8	9,2	26,3	2,9	-4,6	0,39
3	2,292*2,927	5	I	20	5,3	16,0	14,7	1,1	0,3	0
4	2,928*3,563	3	0	12	0	18,0	5,3	3,4	5,3	0;34
5	3,564+4,199	9	0	36	0	21,6	1,6	13,7	' И,4	1,14
6	4,20+4,835	3	г	12	5,3	14,4	2,1	6,6	8,3	2.51
7	4,836+5,471	I	0	4	0	8,4	1,1	8,0	9.0	0,Г9

6

______ ~2 7Т 7 8“ 6 7 7 ’» 8™ 7” 9~7 1оТ II 8 5,472*6,110 I 0 4 0 3,6 0,5 9,9 9,9 0,23 9 - - - - - 1,2 - - - - 10 — — — — — 1,2 — — — — 25 19 100 100 100 100 - - 4,65

Последняя графа табл. I заполняется значениями информативности каждого признака в каждом интервале.

*

Согласно формуле Кульбака величина информативности L -го диапазона j -го признака равна

где    -    вероятность    (сглаженная    частота)    попадания

соответственно в группу А и 3 с -го интервала j -го параметра.

Информативность показателя "скорость течения" в первом интервале (1,020+1,655) определяется так:

8,2'.

Г ₍7,2 2 100

Л

100

1*71

Информативность этого признака в целом находится путем суммирования значений информативности в интервалах

H*j) - f wj),

откуда для скорости течения информативность составила {7_у * 4,65.

Аналогичные расчеты, проведенные для параметров (/, р ,    ,

^ , позволили расположить их по степени влияния на й следующим образом:

О (у/)* 4,65; Щт 3,90; Jfij. 1,49;    1,44;

j(d). 0,77.

Оценка информативности проводилась с учетом изменения коэф-

7

фициента гидравлического сопротивления Л , характеризующего весь диапазон режимов течения.

С целью проведения гидравлических расчетов з реальных условиях помимо определения влияющих факторов на течение необходимо разделить зоны течения. Для решения этой задачи применяются классификационные методы.

2. ПРИМЕНЕНИЕ КДАССИФИКАЦИОННЫХ МЕТОДОВ К ВОПРОСАМ ПРОГНОЗИРОВАНИЯ ХАРАКТЕРИСТИК ПОТОКОВ

Определение границы измени ния режима течения жидкостей имеет важное значение при выборе той или иной аппроксимационной модели при проведении гидравлических расчётов трубопроводов. Известно, что режимы течения определяются многими параметрами, рассмотрение которых в совокупности вызывает значительные затруднения. В таких ситуациях целесообразно пользоваться методами классификации и распознавания образов.

При выявлении двух характерных областей течения может быть эффективно использован метод потенциальных функций, который применим даже тогда, когда исходная информация нс подчиняется закону нормального распределения. Этот метод позволяет при наличии информации об экспериментах, относительно которых известно, к каким зонам течения они относятся (процесс обучения), диагностировать зоны течения в процессе проведения новых экспериментов (процесс распознавания).

В условиях, когда основные факторы, влияющие на исследуемый процесс, сильно коррелируются между собой, трудно установить, по каким из них может быть достигнуто эффективное распознавание режимов течения. В таких случаях удобно производить преобразование исходных данных методом главных компонент. Этот метод применяется также тогда, когда выбор основных факторов усложняется большим

8

числом рассматриваемых признаков.

Известно, что переход от одной области течения (структурной) к другой (турбулентной) происходит не скачкообразно, т.е. существует переходная область течения. Одним из возможных путей диагностирования переходной области является метод построения дендрограмм, позволяющий наилучшим образом разделять объекты на более мелкие однородные группы.

2,1. Метод потенциальных функций

Метод потенциальных функций является одним из методов распознавания с учителем. Применим его к задаче выявления двух характерных зон течения парафинистых нефтей [2^ .

Пример 2.Г

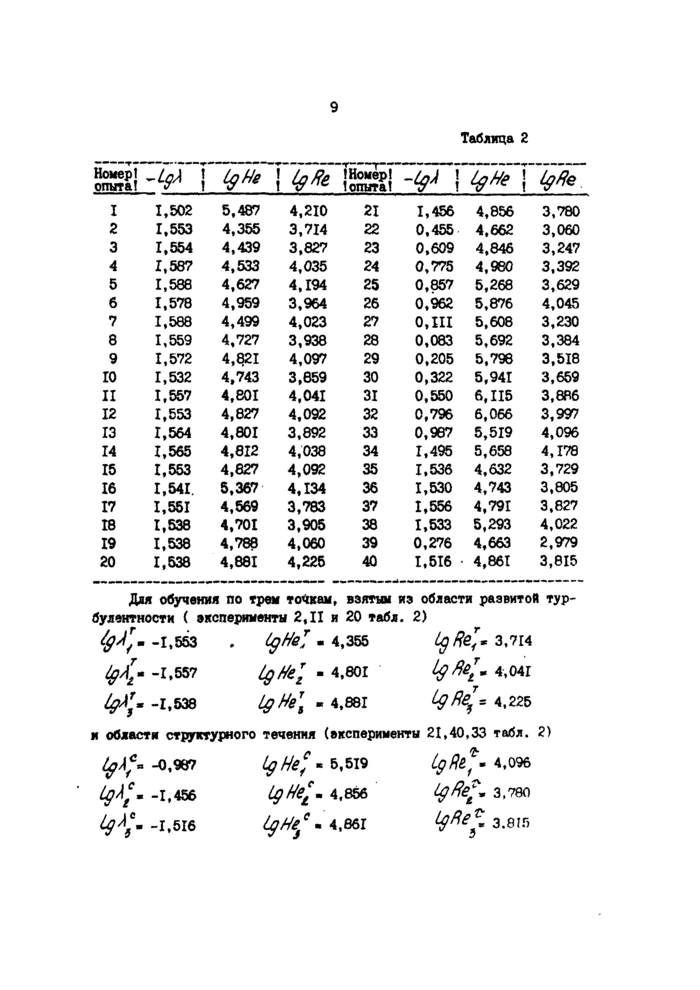
Для статистической обработки используются данные по 40 экспериментам (табл. 2). Представляет интерес определение двух характерных областей течения - структурной и турбулентной.

Ниже все величины, помеченные индексом "Г, относятся к турбулентной области течения, а индексом С - к структурной.

Метод потенциальных функций заключается в следующем. По точкам, взятым в основу обучения * строятся специальным образом потен-

7    *

циальные функции Д и /Г (их построение приводится ниже). За критерий отнесения к той или иной области принимается выполнение неравенства Д ⁷ > Д^е или Д >Д^Г при подставлении в Д

с

и Л параметров экзаменуемой точки. В первом случае экзаменуемый объект относится к области турбулентного течения, во втором - к структурной области.

Процедура распознавания производится в следующей последовательности.

7    с

I. Построение потенциальных функций Д и Д по точкам обу

чения .

Таблица 2

Номер! . опыта! 1 1 I 1 1 ! ШомерТ . 1опыта! -¥ 1 1#Не | 1дЯе, I 1,502 5,487 4,210 21 1,456 4,856 3,780 2 1,553 4,355 3,714 22 0,455 4,662 3,060 3 1,554 4,439 3,827 23 0,609 4,846 3,247 4 1,587 4,533 4,035 24 0,775 4,980 3,392 5 1,588 4,627 4,194 25 0,857 5,268 3,629 б 1,578 4,959 3,964 26 0,962 5,876 4,045 7 1,588 4,499 4,023 27 0,Ш 5,608 3,230 8 1,559 4,727 3,938 28 0,083 5,692 3,384 9 1,572 4,821 4,097 29 0,205 5,798 3,518 10 1,532 4,743 3,859 30 0,322 5,941 3,659 II 1,557 4,801 4,041 31 0,550 6,115 3,886 12 1,553 4,827 4,092 32 0,796 6,066 3,997 13 1,564 4,801 3,892 33 0,987 5,519 4,096 14 1,565 4,812 4,038 34 1,495 5,658 4,178 15 1,553 4,827 4,092 35 1,536 4,632 3,729 16 1,541. 5,367 4,134 36 1,530 4,743 3,805 17 1,551 4,569 3,783 37 1,556 4,791 3,827 18 1,538 4,701 3,905 38 1,533 5,293 4,022 19 1,538 4,788 4,060 39 0,276 4,663 2,979 20 1,538 4,881 4,225 40 1,516 • 4,861 3,815 Для обучения по трем точкам, взятым из области t развитой тур- буяентности ( эксперименты 2,11 и 20 табл. 2) К- -1,553 # tgHe* ш 4 ,355 3,714 Ж -1,557 1д#етг - 4 ,801 % 4,041 -1,538 1дНе\ -4, ,881 , = 4,225 и области структурного течения (эксперименты 21,40, 33 табл. 2) К- -0,987 Lg Не° - 5, ,519 (■9&, Ъш 4,096 К- -1,456 СдНе^ш 4, ,856 % 3,780 К- -1,516 LgHe*ш 4, ,861 (две Тг * 3.815 5