Р 600-86
Методика автоматизированной обработки статистической информации об изменчивых факторах, учитываемых в расчетах надежности конструкций магистральных трубопроводов

МИНИСТЕРСТВО СТРОИТЕЛЬСТВА ПРЕДПРИЯТИЙ НЕФТЯНОЙ И ГАЗОВОЙ ПРОМЫШЛЕННОСТИ

ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ПО СТРОИТЕЛЬСТВУ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ

ВНИИСТ

МЕТОДИКА

АВТОМАТИЗИРОВАННОЙ ОБРАБОТКИ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ ОБ ИЗМЕНЧИВ|ЫХ ФАКТОРАХ, УЧИТЫВАЕМЫХ В РАСЧЕТАХ НАДЕЖНОСТИ КОНСТРУКЦИЙ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ

Р 600-86

Москва 1987

Настоящий документ устанавливает апосоон обработки статистической информации об изменичишх факторах, учитываемых в расчетах надежности конструкций трубопроводов, и содержит соответствующие алгоритмы решения задач обраооташ информации на ЭШ.

Методика разработана оотрудишеаи стлала прочности и надедюости конструкций магистральных труоопро водов и лаборатории математических нетаядв-ивследоиан канд^техн.наук В.Д.Шапиро, зав.гпганси 1 аиясои Кандидатами технических наук В.В.Рожлественокнм Е.И.Федеровым, мл. научн. сотрудниками Г.М. Каайлов», В.И.Васильева*, ст.ииж. Д,Г. Холстово#,

(г) Воеооювннй научно-исследовательский ивсдата по строи viy тельотву магистральных трубопроводов (ЯНЮТ},1987

Выражения (33) и (34) не содержат параметра- CL. Так как

получаем условие    ,    .    „

F₃-F_Z(2F_Z-1}*D,

не содержащее как параметра &    ,    так    и параметра /*.

f(K)-F3-FlUFl-l)

Таким образом, с учетом выражений для F₃ окончательно получаем одно нелинейное уравнение с одним неизвестным К

показал, что в реальном диапазоне значений К она не является монотонной, н уравнение (35) может иметь один - Три корня, поэтому выбор лучшего решения производится с помощью оптимизации по критерию J¹ и иоходя из физических соображений.

После определения значения /г из решения уравнения (35) следует из условия (33) вычислить значение параметра х^:

а также параметров

/

	(36)
if	(37)
к
)	(38)

после чего могут быть вычислены плотность (29) распределения Крицкого-Менкеля, Функция распределения и все необходимые числовые характеристики случайной величины £ (среднее, стандарт, коэффициенты асимметрии и эксцесса и др.).

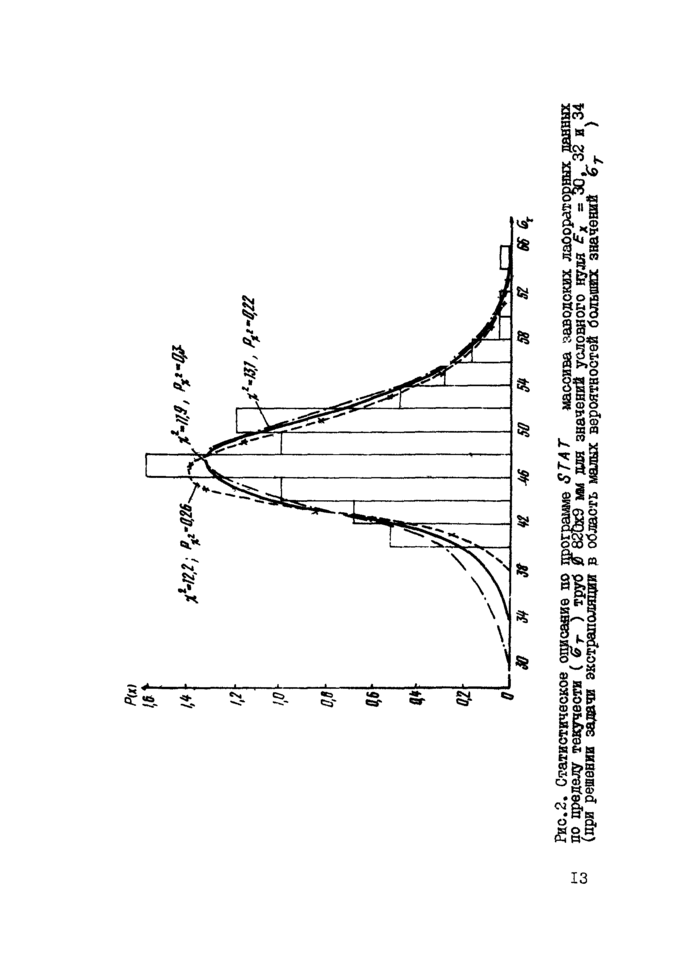
Данное решение реализовано на ЭВМ. На рис.2 приведен пример описания статистических данных о случайной величине проч -нооти (пределе текучести) металла впиральвошовных труб диаметром 820x9 ш для нефтегазопроводов с применением кривой Криц-кого-Менкеля.

,s

;о

13

Следует подчеркнуть, что на этапе подготовки статистических данных к обработке по программе STAT , помимо формирования гистограммы, должно быть зафиксировано крайнее (минимальное или максимальное - в зависимости от задачи) значение случайной величины, так называемый условный нуль. Вабор условного нуля производится с той стороны от гистограммы, с которой не предусматривается экстраполяция в область малых вероятностей. Ери этом взаимное расположение на оси абсцисс самой гистограммы и условного нуля с точки зрения области определения гамма-функции не играет роли, так как в программе предусмотрено приведение теоретической кривой распределения к стандартному виду.

Как показал анализ, точность выбора условного нуля в определенных пределах мало влияет на асимптотический хвост распределения, в чем можно убедиться (например, из рис.2) по близости значений критерия согласия для 3 вариантов значений условного нуля.

3. ОБРАБОТКА СТАЖтаЧВСЮК СВЕДЕНИЙ СБ ИЗМЕШШХ ФАКТОРАХ, ПРЕДСТАВШЕШХ В ШДЕ СЛУЧАЙНЫХ ФУНКЦИЙ И ПРОЦЕССОВ (ПРОГРАММА 0R7R0)

Программа ONTRQ , предназначенная для обработки ста^ тистической информации о случайных функциях, решает задачу расчета характеристик стационарной случайной функции, заданной совокупностью реализаций [з]. Метод решения заключается р сведении случайных функций к системе случайных величин и определения второе смешанных моментов о последующим составлением матрицы корреляционных моментов.

В качестве массивов наблюдений здесь могут фигурировать данные о случайных радиусах упругого изгиба по длине трубопровода, значения механических характеристик грунтов вдоль трассы, колебания нагрузок во времени (при установившемся режиме работы трубопровода) и другие сведения.

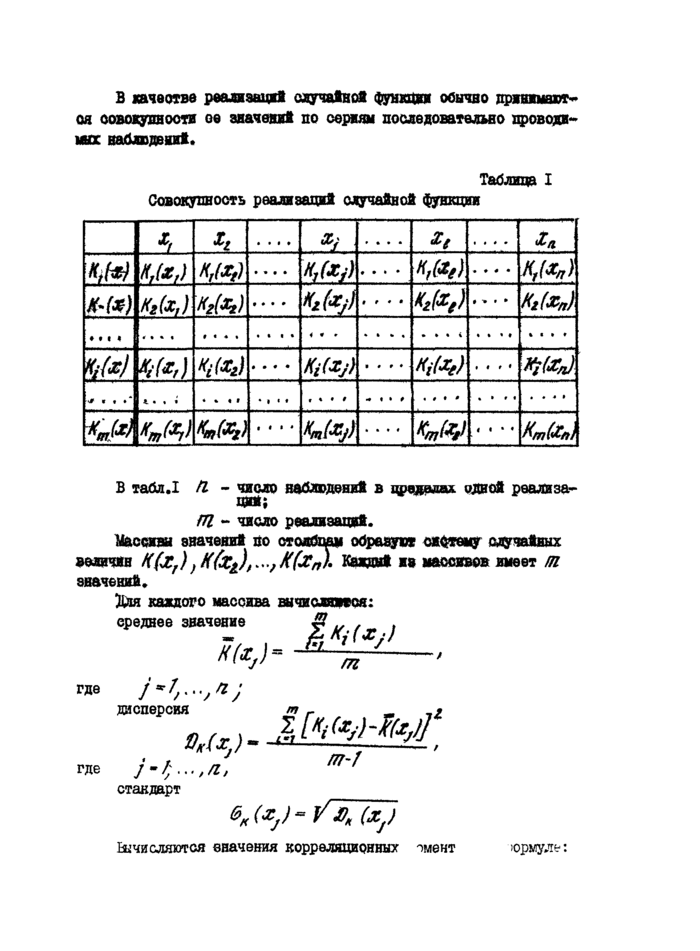
Зарегистрированные значения случайной функции H_r (Xj } заносятся в табл.1, каждая строка которой соответствует определенной реализации случайной функции, а чиояо отрок соответствует числу наблюдаемых реализаций.

14

В качестве рвали задай случайной функции обычно принимаются совокупности ое значений но серины последовательно проводимо: наблюдений.

Таблица I Совокупность реализаций случайной функции

X / хг Л' » « t • Xi % t * • X/i щш Щ) к,(Ы * • • • . • « • KfW Ъ(*,) Кг(Яг) » ♦ * » t г • • Kzfeg) # -» « * Kz(&n) Щ{х) ¥*,) (^г) • • • • Ki(xj) ■ # f * Hi(Xg) • t t * ># * • • л. • « * * % « # * * « • » » ♦ » •• « • t . # • • » » * • 1.41 *тЩ *тЪ> • • • * 4/^ • ■ * * i « • *

В табл.1 tl - число наблюдений в цредодая. одной рвализа-

14 - число реализаций.

Массива значений до столбцу образуют снятому сфзайных

величин K(x_f))    (Х_п).    Каадий    из    массивов    имеет    т

значений.

31ля каждого массива вычисляется:

среднее значение    Щ .

*    ZtKjiX:}

т

где /

дисперсия

Щ)-^ж 7

4    "/ шт    _    Т

0'Ш-Лшм.

где

а,    ^т'⁷

(Xj)

стандарт ¹

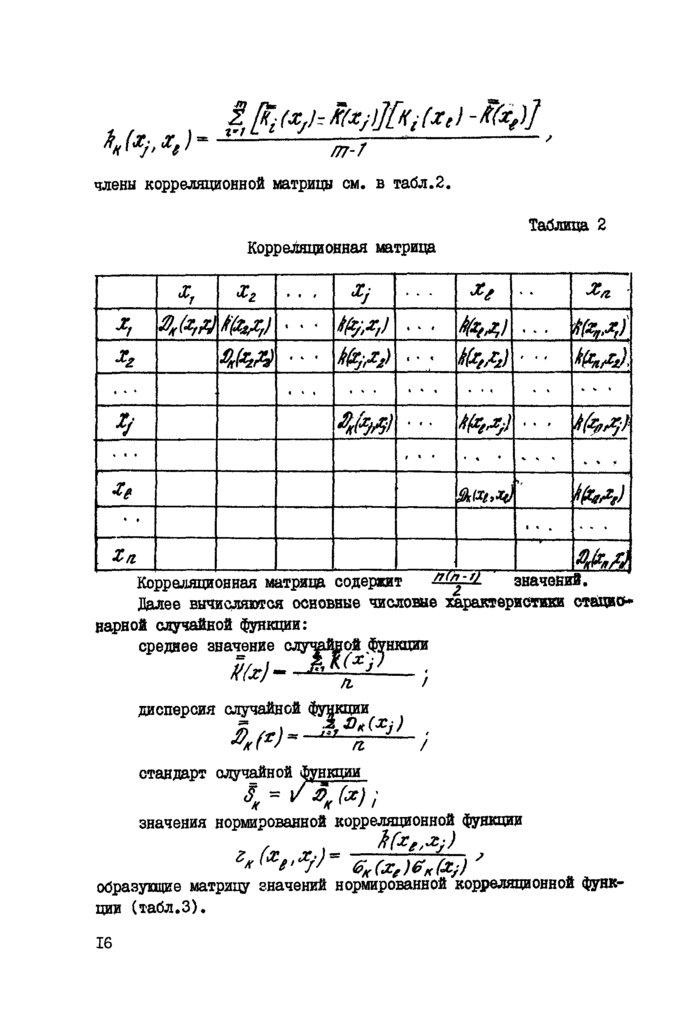
% [к_£ (Xjj- J((Xj}J[h_i fx_e)~

^xt) “ ~    ffFr

члены корреляционной матрицы см. в табл.2.

Корреляционная матрица Таблица 2

4 хг > • > * . . \ « 4 И'М 1 » * им t » « HfM * * * хг 1 t • им 1 * « им • « # HQm). 1 * ' « » « % ь • « * * • • % % % * п(м % • % » » « • * • \ S ' * * « Ze tj • » | % 4 . . . Za

—„----------- —~ ¹    г    _

Далее вычисляются основные числовые характеристики стадией-нарной случайной функции:

среднее значение случайной функции

дисперсия случайной функции

2?    .    .2    Ю¹(£;)

к ¹ /

стандарт случайной функции

I - /4.^(х> /'

значения норшрованной корреляционной функции

_г /ш -i, _,

^Z«^{Xt'^XJ^} 0_К(х,)0_КШ

образующие матрицу значений нормированной корреляционной функции (табл.З).

16

Гайщща 3

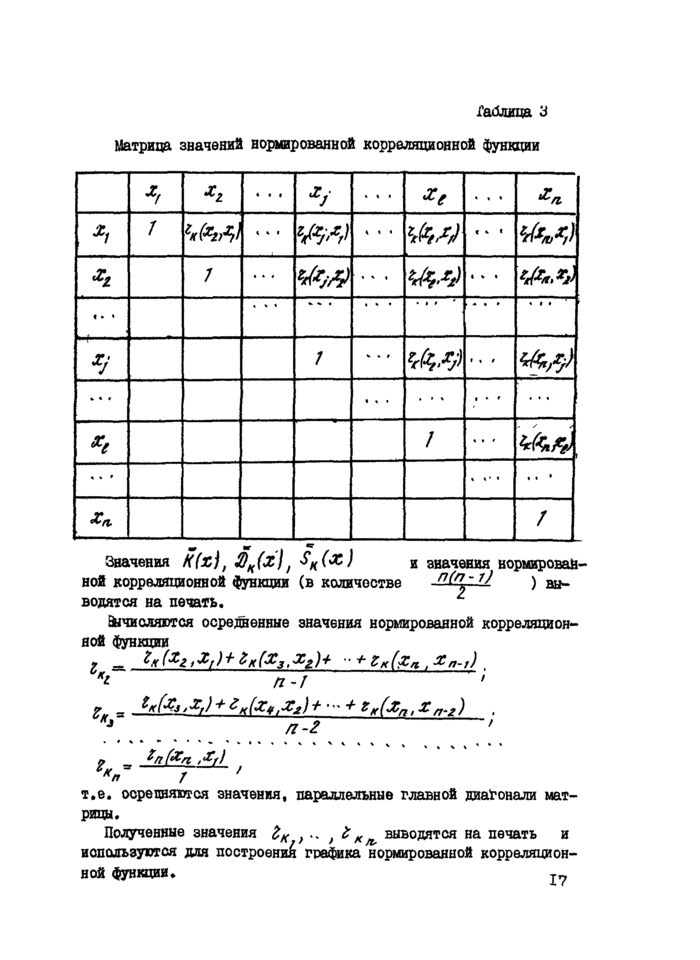
Матрица значений но|шрованной корреляционной функции

Значения K(zj, S)_K(xj_t S_K(x) и значения нормированной корреляционной функции (в количестве    ~    ^    )    выводятся на печать.    ^

Вычисляются осредненнне значения нормированной корреляционной функции

Z — ^x('2’liX,) + ^к(Х₃,Х_г)+ ■■ + Z_K(Xa , Xn-t) ,

*1    n-J    '

Zu = ^x(Xj ,X_r) + Z_K(x<f'Я_£) + •- + Z к(Х_п,£ _п._г)    ,

*^a    П-2    '

Z/i fan ,£,)

7    '

т.е. оореднятеоя значения, параллельные главной диагонали мат

рицы.

Подученные значения Z_{K }} .. _f Z _K/v выводятся на печать и используются для построений графика нормированной корреляционной функции.    _т~

ЛИТЕРАТУРА

1.    Митропольский А. К. Техника статистических вычислений. - М.: Наука, 1971.

2.    Крицкий С . Н . , Ненкель М . Ф . Гидрологические основы речной гидротехники. - Изд. АН СССР,1950.

3.    Вентцель Е.С. Теория вероятностей. - М.: Наука, 1989.

4.    М у * л е р Р. А. К вопросу определения коэффициентов однородности и перегрузки но статистическим данным. В сб.:"Вопросы безопасности и прочности строительных конструкций. М.: ЦНИИПС, 1952.

5.    Константинов Н.М. Гидрология и гидрометрия. - М.: Высшая школа, I960.

19

CCtiEf’BAHHE

1.    Общие положения.................................

2.    Обработка статистические сведение об измен

чивых факторах, представляемых в виде, случайных величин ...............................

2.1,    Обработка информации с применением рас- . пределения Грама-шарлье tпрограммаООКНВ)...

2.2.    Обработка информации с применением распределения Крицкого-Менкеля (програша

3. Обработка статистических сведений об изменчивых факторах, представляемых в виде случайных фунв-ций и процессов (програша uNTRu ) ..........

Литература.......................................

20

Методика

автоматизированной обработки статистической информации об изменчивых факторах, учитываемых в расчетах надежности конструкций магистральных трубопроводов

Р 600-86 Издание ВНИИСТа

Редактор ё.Д. Остаева Корректор .Беликова Технический редактор Т.Л.Фатнова

Л- 105094 По.цписано з печать 23/ХП 1986 Формат 60x84/16 Печ.л. 1,25    Уч.изд.л. 1,1    Бум.л. 0,625

Тираж 450 экз.    Цена    II коп.    Заказ 177

Ротапринт ВНИИСТа

сведений об изменчивых факторах образуют массивы исходной статистической информаций дли расчета характеристик этих случайных величин и функций.

В процессе проводимых отделом прочности и надежности конструкций трубопроводов ВНИИСТа исследований в области, конструктивной надежности лабораторией математических методов исследований разработан ряд программ дня ЭШ типа ЕС по обработке информации об указанных выше статистически изменчивых факторах.

Разработанный комплекс програш является частью системы сбора н обработки информации для расчетов надежности конструкций магистральных трубопроводов.

В настоящей раооте приводится описание разработанных отделом прочности и надежности алгоритмов 3 основных программ ука данного комплекса. С учетом задач отрасли разработан также ряд модификаций программы 00НЫ8^учитывапцях возможность поэлементного ввода данных, обработки массива данных во подвыборкам (для целей статистического производственного контроля), программа обработки случайных функций, обладающих свойством эргодичности и др.

С разработкой настоящих программ не исключается применение стандартных программ обработки статистической информации, входящих в математическое обеспечение ЭШ типа ЕС. Разработанные ВНИИСТом программы унифицируют процедуру обработки информации, исключают в большинстве случаев необходимость подбора подходящих для теоретического описания кривых распределения. Это связано с тем, что возможности стандартных программ при обработке реальных статистик ограничены: кривые распределении, как правило, подбираются лишь по 2 параметрам, поэтому часто требуется проводить перебор различных типов кривых, чтобы удовлетворить критерию согласия. Применяемые в программах ВНИИСТа кривые распределения являются значительно более гибкими, поскольку теоретическое описание для них выполнявшая ПО 3 или 4 параметрам, что обеспечивает достаточную универоальнооть метода. Столь же простой и удобной для применения яалиется также разработанная црограша обработки сведений о стационарных или. близких к стационарным случайных функциях и прощеасах.

Указанные преимущества разработанных ВНЯИНвм программ до-ют основание полагать, что они найдут достаточно вшрокое ирга-

нение для решения трудоемких в вычислительном отношении задач анимационного ооешечевия отрасли.

2. ОБРАБОТКА СТАТИСТИЧЕСКИХ СВДЕШВ ОБ ИЗМЕНЧИШХ ФАКТОРАХ, ПРЕДОТАВЛЯТШХ В ВИДЕ СЛУЧАЙНЫХ БЕЛИЧИЙ

Исходная информация о случайной величине представляется в виде гиотограымы.т.е.стаТястичеокого распределения наблюдаемых частот появления случайной величинн по интервалам ее значений.

В зависимости от цели обработки и характера описываемой случайной величины статистическая обработка информации производится либо с использованием распределения Грама-Шарлье (тип А) [I ], либо с помощью распределения Крицкого-Менкеля (3-параыет-рическая модификация гадаа-распределения) [2\

2.1. Обработка информации с применением распределения , Грама-Шарлье (программа ООНN6 )

Прогрею© QOKNG предназначенная для обработки статистической информации о случайных величинах, имеющих распределения, близкие к вормальаому, решает задачу теоретического описания статистических наблюдений о помощью кривой Грама-Шарлье о последующей проверкой Согласия статистического и теоретического распределений по критерию Пирсона

Обработка статистической информации для любых случайных величин производится по единой схеме:

определение числовых характеристик распределения; расчет теоретических ординат функций и плотности распределения;

определение выравнивающих^частот, их сравнение с наблюдав-' мыми частотами и проверка согласования теоретического и опытно*-го распределения по критерию /^г.

Исходными данными для расчета по этой программе являются сведения, характеризующие данную выборку, представленную в виде гистограшы:

К - число интервалов;

Xj - середины интервалов;

5

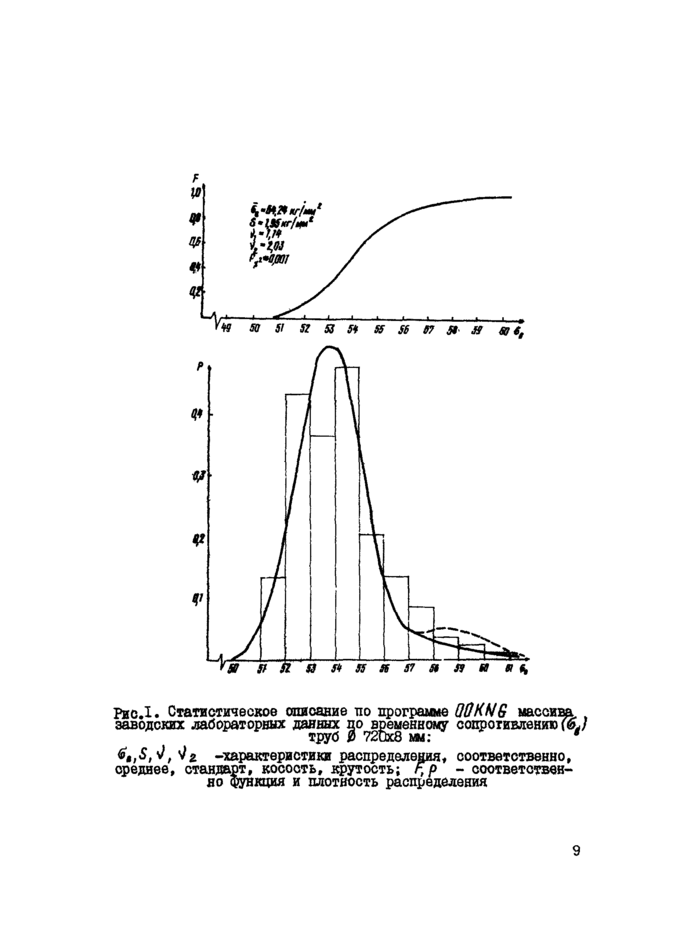
На рис.I приведен пример использования программы DOftNt! при статистическом описании сведений о прочности материала труб для магистральных трубопроводов. При описании некоторых массивов данных по указанной программе (как и в приведенном на рисунке примере) наблюдается биение теоретической кривой в хвостах распределения, что несколько снижает эффективность описания статистических данных кривой Грама-Шарлье. Для таких случаев следует применять программу STAT , не имеющую указанно-* го недостатка.

2.2. Обработка информации с применением распределения Крицкого-Менкеля (програша STAT)

Программа STAT решает задачу теоретического описания непрерывных случайных величин по выборочным данным, представленным в виде гистограммы, с последувдей проверкой согласия по критерию jf . В отличие от описанных в п.2.1 кривых, областью определения которых является вся числовая ось, кривые -Крицкого-Менкеля имеют одностороннее (справа или слева) ограничение. Существенное преимущество метода - Гарантированная гладкость кривых распределения в области малых вероятностей на асимптотическом хвосте. Данные кривые являются трехпараметрич©-скими. В основе кривых лежит гамма-распределение с плотностью

= ~ *е~^Х;    (23)

и функцией распределения    ^х

F(x)~ ~} /Х^Г~^Ге*tte,    (24)

fl/J о

Первые три начальных момента гамма-распределения вычисляются по формулам:

Щ - Г /'

m_z ~r(r+r),    ⁽²⁵⁾

„    т_л*г(зч-гНг+2)    ,

Лиспорсия гамма-распределения равна:

б^г ~/п₂ -т* =у* -

Для получения трехщраметрической кривой распределения используют функцию:

6_tlS, 'Jf'Jz -характеристики распределена, соответственно, ореднее, стандарт, косость, крутость; г, р - соответственно функция и плотность распределения

9

1

'

1кчисляются значения корреляционных омент