щщИСТЕРСТЮ СТРОИТЕЛЬСТВА. ПРКДЩЧаЯШЯ }ШЬТЯНОЙ И ГАЗОВОЙ ПР01ШШН0СТИ

BoscodshhS научно-деоледоватадмкяй инствту* до строительств., жгистральных трубопроводов

НЕТОдаКА С ПРОГРАШОЙ РАСЧЕТА НА ЭВМ П7Б0ПР0В0Д0В ПРИ ПУЛЬСАЦИИ ДАВЛЕНИЯ

Москва - 1983

I*.

3*5. Подземные трубопроводы моделируют элементами типа ТРУБА, на линвйноупругом основании. Коэффициенты постели упругого основания вычислят по формулам

/3.3/

/3,4/

Здесь D_M - наружный диаметр трубы, см;

С₀ - коэффициент нормального сопротивления грунта, кгс/сМ^;

С„ - коэффициент касательного сопротивления грунта, кгс/см^.

Значения С» и С* принимает теми же, что использованы в статическом расчете.

3.6, Явные выражения для элементов матрицы жесткости в местной систем» координат криволинейного элемента весьма громоздки и неудобны при вычислениях. Поэтому для их численного определения на •ЭВД используется следующий алгоритм.

Интегрирование уравнений напряженного состояния криволинейного стержня даёт

lP№HA«]lc}i М-[в«]И,

где [(Щ ,    “    векторы    усилий и перемещений соответст

венно размерности б;

- вектор постоянных интегрирования длины 12;

[ACs^CeCs)] - матрицы размерности 6x12, выражения для которых приведены в приложении 3.

Для узловых усилий и перемещений получаются выражения

1C н>г И..

[р№К*П^ц]*^ш£^кН^и1’

II-

гда    CKMtflfX]'¹    №

- матрица жесткости криволинейного элемента в местной системе координат. Матрицы С^З и М3 приведены в приложении 3.

3.7. Для определения матрицы инерции криволинейного элемента используется выражение для кинетической анергии

T*£j>Fj

где

4j>F{u£ [ f[xr^T[8]^T[S][6][X]'^jds]lu

где

«а

M=pF Ux]‘^lT[8]^T[&][6][xfcls

^Г -t    /3-⁶/

- матрица инерции, элементы которой вычисляется с помощью процедур численного интегрирования.

3»8* Дямге^1груп1[1тй свойства трубопровода следует учитывать» зада для элемента ТРУБА. коэффициент демпфирования £    .    В    прог

ни расчета матрицу дешфщюваниам получают умножением матрицы Шюсти для данного едемента в местной системе координат на коэф-ДОНГ дм*^ярпяаи« /^ f

/3.7/

Валитова коэ$фицаанта лемпфцюванин ^ ^{свяаана} оо зиачвня-цлсга.рф«яч8вяого дацреыента    соотношением

/? = -r/v7ti    /3.8/

С Ж Г

pi /j7_t - „ ts_/t - элементы матрицы масс я матрицы жесткости.

Црн отсутствии экспериментальных данных значение дедамента Колебаний для стальных однослойных сварных и бесшовных труб допус-Мвтся принимать равным ^ш 0*005»

3»9» Конструкцию опоры трубопровода /представляющую собой узел давления трубы и опорному фундаменту/ моделируют в расчетной схеме цементом ОПОРА* для которого задают в местной системе координат Воступательные жесткости С_Х) Су_} Се • кгс/см и вращательные Меткости flv, /у    *    яро*см» В случае* если жесткость опори в одном из направлений превышает величину    /г^/где

1_г ь £ '"момент инерции сечения в длина элемента трубы» примыкающего к данной опоре/ в IQ⁸ или более раз» соответствующую степень свободы узла давления устраняют из рассмотрения /т.е. считают опору неподвижной в соответствующем направлении/»

Коэффициенты демпфирования в опоре ^    /    с    *!,..• ,6/зада

ют отдельно для каждого направления поступательного и вращательного

3»10» Массивный фундамент опоры моделируют элементом ГЛАССА,

14.

Задают масс^ фундамента гП^ , кге^/см и массовые моменты инерции Относительно главных центральных осей в местной системе координат

L, 1#, 1_г • ^гго*°²*^с“-

3.II, Естественное основание иод опорный фундамент моделируют элементом ОПОРА* Основную упругую характеристику естественных оснований фундаментов под опоры - коэффициент упругого равномерного охарил определяют оогашсно главе СНхП П-19-79 по Формуле

С--&£_г (4+ /f_o/F_ncf> ) кго/ои* /3.9/

Здесь , см^-1 - коэффициент* принимаемый равным: для песков - 0*01, дня супесей и суглинков - 0,012, для глин и црупноо<5ло-мочиых хрунтов - 0,015;

£_г - модуль деформации хрунта, кгс/см², определяемый в соответствии о требованиями главы СШй^^ошшф^Зшю ооневашй-щтл и оооруаений;

р    - площадь подошвы фундамента, см²;

F    ** 1*10^ см².

влияние ооковой еясыттки фундамента на увеличение коэффициента жесткости основания допускается не учитывать.

Коэффициенты упругого неравномерного сжатия , хго/ом*, упругого равномерного сдвига С* , кгс/см* я упругого неравномерного СДВИГа Ру, , КГс/сМ* прттамяяугр^ ряттмшдг

с?-гс2-    с:-с/ ъы

Коэффициенты жесткости для естественных оснований ч Су> определяют по формулам:

J• моменты инерции площади подошвы фундамента соответственно относительно горизонтальной и вертикальной осей, см*.

Значения характеристик демпфирования естественного основания следует определять» как правило» по результатам экспериментов. Соответствующая методика содержится в Руководстве / 3]•

Допускается при отсутствии опытных данных принимать значение коэффициента демпфирования при вертикальных колебаниях ^ о 0»005 - 0,008 о.

Значения £ , соответствующие горизонтально-вращательным колебаниям фундаментов в 1,5-2 раза ниже значения П₂ •

3.12» Опорные металлоконструкции трубопроводной обвязки моделируют с использованием стержневых элементов БАЛКА., для которых задают длину £ , геометрические характеристики сечения FJ*,

Jy_} местной системе координат, распределенную массу /77 и свойства материала £jp .

Ненулевые элементы симметричной матрицы жесткости К элемента ВАЛКА, имеют ввд|

16,

Элемент Anj матрицы жесткости представляет собой узловое ДОше в налрятигашпу l вря единичном смещении в направлении J • Элементы симметричной матрицы инерции балочного элемента имеют

/77/, ^    ^    т_гг-

/зле/

Коэффициент демпфирования для опорных металлоконструкций при Ксутствии опытных данных допускается принимать равным

/3.17/

ДО uj - частота вынуждающей нагрузки,

3,13, Свайные фундаменты под опоры рассчитывают, моделируя ■ваю сосредоточенной массой /т? , которую находят до формуле

т =-р*щс_й    /зле/

до /Па - масса сваи, кто* о²/см^

Jh** O_t4+!,£>£

- длина свах, м.

Коэффициенты жесткости свайного основания в вертикальном _и Юризонтакьнсм направлении Кх - Ку вычисляют согласно главе СНиП И9-79,

Коэффициенты демпфирования _t ij_y , tj_L для свайной опоры Донимают равными

1* - o.vfxT

°'^г / f;    /3.20/

3.14.    Массивные узлы трубопроводной арматуры моделируют элементов МАССА, который характеризуется значениями массы т и массовых элементов инерции I* ,1 у Т* . определяемых в необходимых случаях опытным или расчетным путем по известным формулам теоретической механики»

3.15.    На основе исходных данных, характеризую:дих топологические, геометрические и механические свойства системы и ее элементов, в программном комплексе происходит автоматическое формирование динамической матрицы с помощью ЭВМ.

Вначале матрицу жесткости каздого элемента в местной системе Координат К' получают по указаннш в п.п 3.3 - 3.14 данным. Матрицу жесткости элемента преобразуют затем к общей системе координат:

К - tVt    /3.2Х/

Верхний индекс Т означает транспонирование;

Т - клеточно-диагональная матрица преобразования, элементы которой составлены из матриц направляющих косинусов А и матриц переноса начала координат Ri и соответственно для ппрвого и второго концов элемента

Матрицу масс М ''ж матрицу демпфирования В ^в местной системе Координат преобразуют к общей системе координат по зависимости, аналогичной /3.21/.

Цроцедуры преобразования матриц жесткости, инерции и демпфирования к общей системе координат повторяют для всех узлов и автоматически компонуют полную динамическую матрицу системы.

4. Расчаты овободншс и вштимшл колайаыий

4.1* Частоты х формы свободных колебаний трубопроводной системы являются важнейшими динамическими характеристиками» позволяющими получить информацию о свойствах объекта* Для расчета свободных колебаний достаточно иметь информацию о жеотхости и инерционных характеристиках системы» содержащуюся в разделе 3*

4*2* Уравнение движения системы со многими степенями свободы сводится к следующему

/4.1/

Здесь X - вектор-столбец динамичеохих перемещений и углов поворота в узлах системы; точки обзпачают цроизводные по времени;

м - матрица инерции;

К - матрица жесткости;

3    -    матрица    демпфирования;

- вектор возмущающих узловых нагрузок.

Уравнение /4*1/ служит для расчета вынужденных колебаний при действии периодически изменяющихся во времени нагрузок.

4*3* Уравнения дмпевтиг щщ мадшт свободных колебаниях в системе без учета трения можно представить в виде

Мк'+К*-‘0

фвдения Г и демпфирования В приближаются к нулю. Решение JC принимается в виде

ос - Re {. re^LP*J

Здесь lt    - вектор-столбец неизвестных    амплитуд;

Р    - неизвестная частота;

L - f3i

19,

Re - действительная чает* комплексного числа*

Подстановка решения /А*2/ в уравнение /4.2/ приводит к задача ц собственных значениях

(К-Р'м)^1г'0    /1.4/

Система /3*4/ ищет ненулевые решения» если определитель тт-ркщ умноженной на вектор tr _# равен нуле» т.е.

p/e-i (К-Р¹М):0    /4.3/

Уравнение /4*5/ относительно р^г представляет собой частот-* Ное уравнение#

4*4* Для отпевания собственных значений приманен еладуздй алгоритм [2/* Сишзтричнув матрицу II представляют в виде произведения квух "треукмшных* матриц!

M-L^rL    /W

f/t - индекс» обозначающий транспонированную матрицу/.

Задача о собственных значениях /3.4/ принимает вид

(А-Р^гЕ)г,*0    /4.7/

Здесь

v~< - Lv~

Р ■» Qn, 1ДН и цнд д¹ матрица.

Далее для получения собственных значений и собственных векторов выполнено обращение к стандартной подпрограмме Ь10- ЕЛ/» реа-■вдующей метод вращений АЛ

Каждому из п собственных значений р\ соответствует соб-■Ввепный вектор V\ • Пусть ооботвенный вектор УЦ имеет эле» MTU Vj^ • Квадратная матрица V » каждый столбец которой

является собственно! вектором

V= [irjKj'i_h    /4.8/

доставляет собой модальную матрицу для задачи о собственных значениях» выдаваемую на печать в результате вычислений*

4*5* Задача о вынужденных колебаниях трубопроводной системы о учетом демпфирования решается на основе уравнения /4.1/:

Мх * Вх ■> К х = Г

При этом возбуждение имеет установившийся гармонический харак

Решение в етрм случае следует искать в виде

сс-    /4.10/

Подотаповва /4*9/ и /4*10/ в уравнение движения /4.1/ приводит к соотношению

(К - и>¹М * 1-шВ)л = А    /4.и/

Введены обозначения

Л-сП - К-ио'ГП-Ишв Л - К-П - iv В

X ~ и i~ Lux

/4.12/

Подстановка /3.12/ в /3.11/ ж решение даю

и = If +n/\~'f)

«г» <Р~' (f- ПЛ-'f)

"Методика е диаграммой расчета иа сЗМ трубопроводов при пульсами давления" разработана отделом прочности и надежности конструкпй щис тральных тт^бопроводов и лабораторией математических методов ис Медования Ж^С1ж при участии кафедры строительной механики коробля Млининг с адского технического института рыбной промышленности и хоэя ига а /КТИРП и 7/.

В "Методпа..." изложена методика расчета собственных к вынужденных холебан£± трубопроводов произвольной пространственной конфигурации.

"Методика..разработана на основании теоретический, экспериментальных исследований и натурных наблщений обвязочных трубопровс дов компрессор£ыд станций и станций подземного хранения газа.

"Методику...” составили! кандидаты технических наук М. С.Гера-тейн, И.Д.Кр£Г7хш, инженэры В.Д.Корнеев, В.Н.Павлов /ВНИИСТ/, Ю.М.СапрыкЕЕ /ZZ2ПиД/, Г.О.Темпель /7вбектрансгаз/.

2Ф.

т

Таким образом, найдено решение в виде вектора-столбца

X - u + tur    /4.14/

Оптимальный по быстродействию алгоритм решения задачи о выну* денных колебаниях, описанный в методических рекомендациях 2 использован в данной методике

иг - (Р-и>^ьО + lo'R)~^j (ЛП''^-f) ,

и -- П~^{ (у-Лиг)    /4.15/

да    ,

Р-П*КП к Q *MIT'K *КП'*М

R -- М1Т'М

/4.Х6/

4.6. В результате расчета по программе на печать выдаются амплитуды перемещений в узлах

CLj - Uj* Wj    /4.17/

I фазы

if, =

V    </    Hi

|уюхидила и ирш. унммия рцо— i г ЗЧЬ’ХЧ

чета яа SBM трубопроводов    __

при пульсашзи давления    ]    Впервые

__|_

OS оци-е тгол-07Усенуу$».

1,1. В документе содержится методика динамического расчета разветвленных трубопроводов произвольной пространственной конфигурации с массивными опорами и арматурой применительно к обвязочным трубопроводам компрессорных станций /КС/, подвергающимся действию пульсаций давления транспортируемого rasa*

1*2* При проектировании и расчете обвязочных трубопроводов ЯС следует выполнять требования главы СНиП П-45-75 "Нормы проектирования, Магистральные трубопроводы" и "Инструкции по расчету обвязочных трубопроводов"* Согласно данной методике выполняется поверочный расчет обвязочных трубопроводов на динамические нагрузки? определяются частоты собственных колебаний и амплитуды виброперемедений при вынужденных колебаниях, вызванных неравномерностью потока транспортируемого продукта*

1.3* Динамические нагрузки на трубопроводную систему, создаваемые в результате неравномерности потока, которая вызвана периодическим воздействием импульсов расхода компрессоров на линиях всасывания и нагнетания, определяются на основе акустического расчета трубопроводных систем по методикам, разрабатываемым специализированными организациями /ВНИИГаз, 11ЖХиШ им* И.М.Губкина и др./*

1.4* Методика включает программы динамического расчета трубопроводной системы на ЗЗД, входящих в единую систему /ЕС ЭЗЦ/* Программы комплекса \J/\/IlST составлены на алгоритмическом языке Ш/1 с использованием методических рекомендаций [2 ] , составленных

ИМАШ АН СССР.

(сева ВНИИСТам I Утверждено ВНИИСТом    !    Срок введения

I 15 октября 1983 года I    в действие _

|    !    "£ "Лг/Л 1984т

■*- — — *-----

5

2. Расчетные одами обвязочных трубопроводов

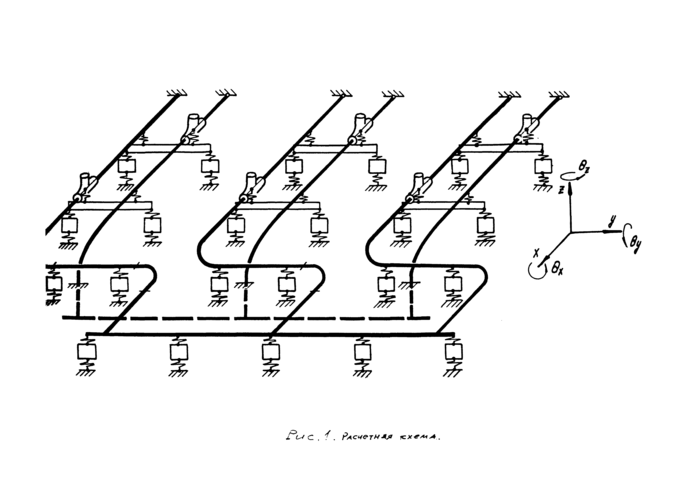
2.1. В качестве расчетной схемы обвязочного трубопровода КС Принята пространственная стержневая система, состоящая из прямолинейных и криволинейных участков постоянной кривизны и включающая массивные сосредоточенные и упруго-демпфирующие элементы. Предусмотрена возможность учета в расчетной схеме различных упругих и демпфирующих свойств трубопроводов, арматуры и опорных конструкций*

Пример расчетной схемы трубопроводной обвязки представлен в аксс&етрической проекции на ряс* I*

2.2* Трубопроводная система считается полностью компенсированной, т.е, принято, что продольные растягивающие усилия в трубах при статическом действии внутреннего давления равны . усилиям на заглушку /произведению давления на площадь трубы "в свету¹*/. Таким образом, цри рассмотрении малых колебаний допустимо использование линейной теории и применим принцип суперпозиции.

2,3. Расчетную схему представляют совокупностью дискретных элементов, взаимодействующих между собой в кон чном числе узловых точек.

Использованы дискретные элементы следующих типов.

Элемент трубы однородного до длине сечения с осевой линией постоянной хфивизны, лежащей в плоскости, которая занимает произвольное положение в пространстве /в программном комплексе элемент носит названии ТРУБА/) элемент прямой трубы /т.е. о осевой линией нулевой Кривиипм/ является частным одучаам элемента ТРУБА)

-    элемент прямолинейного стержня произвольного достоянного по длине сечения /БАЛКА/)

элементы ТРУБА и БАЛКА могут быть свободными между узлами или связанными с упругим основанием;

-    опорный безмассовый элемент конечной протяженности для моделирования уцругих и упруго-демофяруящих опорных конструкций, амортизаторов, грунтового основания иод массивные элементы системы /ОПОРА/;

я.

• инерционный сосредоточенный элемент для моделирования фундаментов под опоры» массивных элементов арматуры - кранов, задвижек -ш Т.п. /МАССА/.

2.4.    Дискретные элементы соединены друг с другом в узлах. Каждому узлу в общем случав соответствует шесть степеней свободы. В задании на расчет указывают номера и координаты углов.

Координаты узловых точек задают в общей оиотеме координат х, у, j • Ооь z принимают направленной вертикально, а направления осей х и у выбирают таким образом, чтобы направляющие векторы осей х, у и z образовали правую тройку.

2.5.    Для трубопроводов /моделируемых элементами ТРУБА/ узлы ведают на опорах, в местах стыковки труб с арматурой, в точках разветвления, а такие в пролетах между опорами /не менее одного узла зюйду соседними опорами/.

Криволинейные участки трубопровода можно моделировать прямолинейными и криволинейными дискретными элементами типа ТРУБА. При использовании криволинейных элементов задают номера и координаты концевых узлов криволинейного участка, а также координаты точки пересечения касательных к осевой линии, проведенных в узловых точках.

При использовании прямолинейных элементов задают номера и^динатн узлов на криволинейной осевой линии.

Подвижные и упругие опоры моделируют элементами типа ОПОРА, дня которых задают номера и координаты концевых узлов.

Для неподвижной опоры задают координату и номер узла. Неподвижным узлам дают номера, большие, чем номера узлов, имеющих степени свободы.

2.6.    С каждым дискретным элементом связывают местную систему координат х , у , jr , направляющие векторы которой образуют правую тройку.

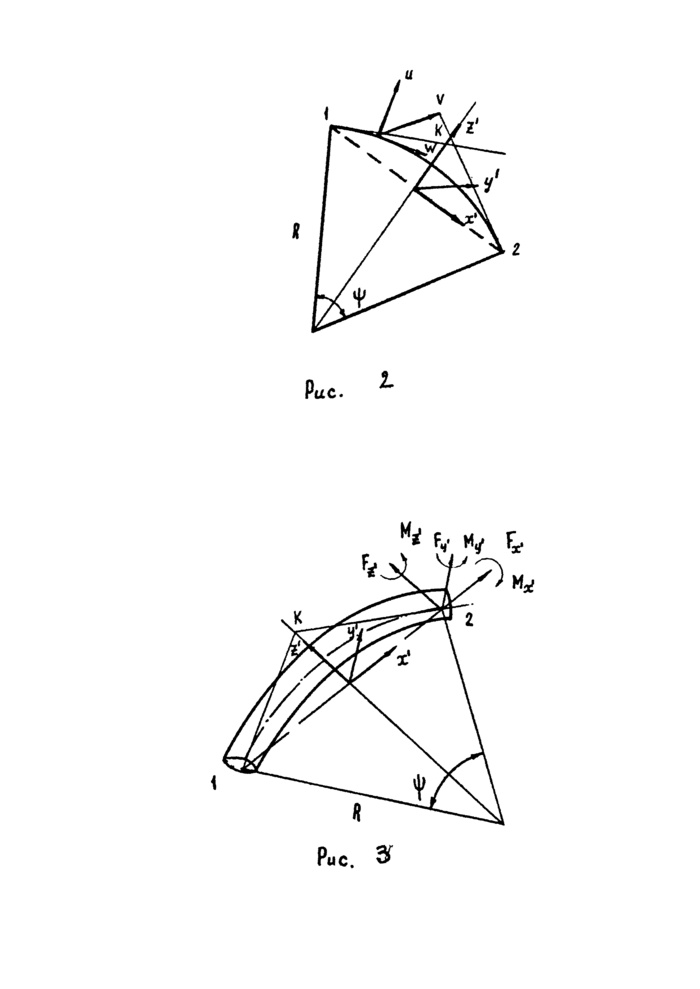
Местную систему координат х'у'/' для элемента ТРУБА определяют

II положения точек L ₉ j и к в общей системе координат так,как 9Т0 показано на рис. 2. Центральный угол криволинейного элемента ткет быть вычислен по координатам концов и заданному радиусу R. ; ОН не должен превышать 90°. Участки о большим углом следует разбивать на два или более элемента.

/ л прямолинейного элемента ТРУБА, ось х * направлена вдоль оси друбс-оэвода от узла с меньшим номером к узлу с большим номером.

Ось у ' выбирают, как правило, лежащей в плоскости х-у общей система координат.

Для элемента БА.ЛКА. ось х ' направлена вдоль оси стержня от узла I меньшим номером к узлу с большим номером _t а оси у ' и    совпа

дают с главными центральными осями поперечного сечения.

Для элемента ОПОРА местную оиотецу координат выбирают, как «равно» совпадающей с местной системой координат одного из элементов тт или ТАЛКА. примыкающих к данной опоре. В некоторых случаях ткет оказаться целесообразным иной выбор местной системы координат, учитывающий конструктивные особенности опоры.

3. Модели ДИСКРОТНЦХ элементов я iTiniMmnMiln.» mmamamm»

3.1. Каждый из дискретных элементов, совокупность которых моделирует трубопроводную обвязку в целом, характеризуется инерционной матрицей, матрицей жесткости ж матрицей демпфирования. Для вычисления этих матриц следует знать физике- де-ехсиические свойства участков и узлов трубопроводной системы. В данном разделе приводятся данные, необходимые для вычисления динамических матриц элементов.

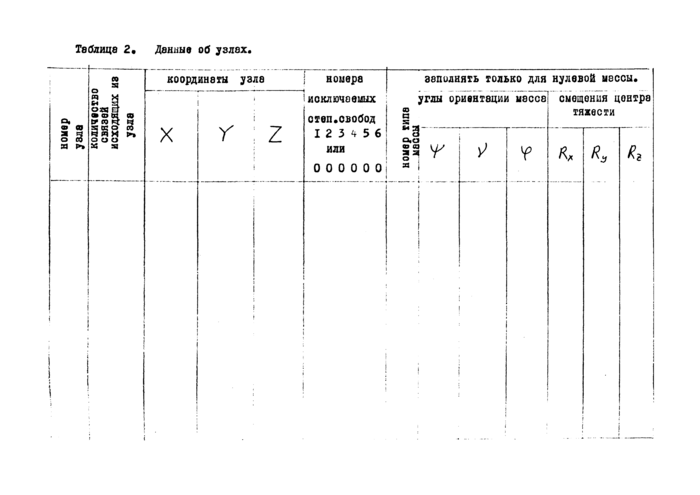
3.2* Основным элементом рассматриваемой системы етъоются произвольно расшоложшшая в пространстве груба с сечением в виде топкого Дояьца я осевой линией, изогнутой в плоскости и имеющей постоянную Ифжвизну, рис. 3 /элемент ТРУБА/.

Лвь

Частным случаем является элемент ТРУБА о нулевой кривизной осевой линии, который соответствует прямолинейному участку трубопро

вода*

3*3* Для элемента ТРУБА задают наружный диаметр трубы J) , толщину стенки трубы d¹, массу единицы жданы т . В общем случае величина ггь включает массу самой трубы, массу изоляции, массу содержащегося в трубе rasa и другие распределенные по длине трубы массы, участвующие в поперечных колебаниях трубы. Задают также модуль упругости Е и коэффициент Пуассона ja материала трубы. Геометрические характеристики - площадь сечения F и моменты инерции сечения /„    ,    я    1_г вычисляются в программе.

Над *]_г донимаются осевые моменты инерции сечения относительно диаметра сечения, под /,    -    полярный    момент    инерции    относи

тельно центра сечения,

3,4, Для элементов, моделирующих криволинейные участки трубопровода /отводу/ моменты инерции при изгибе в плоскости и из плоскости вычисляют умножением величин 1^ к /_д на коэффициент уменьшения жесткости 1^,

В соответствии с главой СНиП^Нормы проектирования, магистральные трубопроводы" как для гнутых, так и для сварных отводов коэффициент kg при ^ 0,3 определяют до формулам!

/3.1/

/3.2/

где о - толщина стенки трубы;

ti - средний радиус сечения;

— радиус изгиба оси.

Значение вычисляют и вводят в числе других исходных данных

в задание на расчет,