МИНИСТЕРСТВО СТРОИТЕЛЬСТВА ПРЕДПРИЯТИИ НЕФТЯНОЙ И ГАЗОВОЙ промышленности

ВсесоюиыЛ научно-исспедоиотельасий институт по строительству магистральных трубопроводов

•ВНИИСТ*

ш

РЕКОМЕНДАЦИИ

ПО РАСЧЕТУ УСИЛИЙ ВНУТРЕННЕГО ЦЕНТРАТОРА ДЛЯ СБОРКИ ТРУБ С НАЧАЛЬНОЙ ОВАЛЬНОСТЬЮ СЕЧЕНИЙ

Р 541-84

Москва 1986

В настоящих Рекомендациях ивложена методика расчета разжимных усилий центрирующего ряда внутреннего центратора с учетом овальности сечений сваривавшее труб.

Данине Рекомендации предназначены для инженерно-технических и научных работников, зачинаю-щихся расчетом и проектированием оборудования для свярочно-монтажных работ.

Рекомендации разработали сотрудники отдела прочности и надежности конструкций трубопроводов ВНИИСТа А.А.Никитин, В.П.Черний и сотрудник лаборатории математических методов исследований ВНИИСТа Т.А.Першийа.

(g) ВсесооэныЙ научно-исследовательский институт

Примечания: I. Правило знаков приважено на рис .2.

2. Вмрахешш для внчивлеаяя коэффициентов    ж

кии совпадают с формулам* для коэффициентов щ_н ж Н}_Н со-ответственно, после замена в нжх г на и. •

Рже.2. Правило жжаюв для компонентов напрясенно* деформированного оостошкя ж оеченяж цилжндржчв -схож оболочки кругового очертянал

Опраюдеаже вождя! «внтоирдаиего вяжа аентватора

2.15. Вначале рассматриваем воадеВствже цеатржружвго ряда на бесжоаечяуж трубу вагруажамж, харахтерняуянвм1 пфе-хенжямж (3) в (6).

Вследствие елмме^аа аадачх жа данном ее erase граняч-нме уславяя ваше паем в виде;

€17)

что приводят к системе четцрех лянеВннк уравнений отноежтелв-но прожавоявнмх постояннмх.

II

Ревекке системы (17) с учетом (16) позволяет получить неизвестные произвольные постоянные Cj выражений (15) и (16) и в итоге значения любых из компонентов перемещений и усилий.

По найденным значениям произвольных постоянных Cj (j =

I, 2, 3, 4) определяем силу M_z(o) , изгибающий момент M_z(q) и перемещение lfi(o) в сечении, совпадающем с плоскостью центрирующего ряда и внутренние силы //j(xJ , A^(Хц) , (2₁(Хц) ,    »    нагибающие    моменты М_}(Хц) * М^Хц) л

перемещение ЩХц) в сечении, находящемся на расстоянии Хц от плоскости центрирующего ряда.

2.16.    Далее рассматриваем пояубесконечную трубу, к торцевому сечению которой приложены силы Н₇(Хц), @(Хц) , S(Xy) и момент М₇(Хц) , определяемые таким образом, чтобы после суммирования их с соответствующими величинами, полученными ранее для этого же сечения в бесконечной оболочке,торец трубы оказался бы свободным от внешних нагрузок. Исходя из зтих соображений, указанные величины, распределенные вдоль торца по закону cos 2ft и Sin 2ft , определены как

N_J(Xn)'*-N₁(x_li)j^ й_г(х_ч)=З_г(х_ц);1    _ffa)

S(^xa) ⁼    М_г(Хц)    =    ~ М^(Хц) •    /

Таким образом,на этом этапе реоения условиями для определения произвольных постоянных для полубесконечной труби являются условия (18), из них находим новые произвольные постоянные Cj ( j - I, 2, 3, 4) с помощью которых, а также выражения (16), могут быть найдены все составляющие напряженно-де -формированного состояния от действия так называемых компеней « рующих нагрузок (18).

2.17.    Используя указания _п.2.16, вычисляем значения сил_ N^ _; изгибающего момента М₂ и радиального перемещения &

в торцевом и совпадающем с плоскостью центрирующего ряда се -чениях полубесконечной трубы от действия компенсирующих нагрузок (18), причем при вычислениях нужно принимать величину = 0 для торцевого сечения и    Я для сечения, сов

падающего с центрирующим рядом.

12

2.21. Так как с процессом выправления овальное» трубы кольцевая нагрузка    не    связана,    то    для опредеяеная мак

симально допустимо! овальности расчетные величины прогиба W₀ находят как суммы результатов только п.п. 2.15 и 2.17.

3. АЛГОРИТМ РАСЧЕТА

За основании разработанной методики 6а составлен алгоритм определения разжимного усилия центратора и допустимо! овальности сечения труби.

Влажная информация

1.    Наружны! диаметр трубя В_н (см);

2.    Толцина стенки fi (см);

3.    Расстояние от торца трубы до плоскости центрирувцего ряжа Хц (см);

А. Предел текучести 6_Т (МПа);

5. Модуль упрувостн £ (МПа);

6. Коэффициент поперечно! деформации    V (б/р);

7.    Отношение 2 =

8.    Коэффициент трения Х^р.

Вычисление промежуточных результатов

1)    Параметры сечения трубы:

I. R- 0,5(1)_и - h), см:

г. a*\/l2(7~U*)

3. t =2\/з/2а ■

*. и = ValZ ;    и/RfckT¹))

5.    д-100Efi³/lZ(7~)}% н.см;

2)    коэффициенты системы линейных'уравнена! для бесконечно! трубы:

6.    a_n=-H~2Vt³;

7.

8.    0_1Ъ=-7)11-2$и³;

э. а_ц = +7)и-2$и³;

IA

10.    Q_Z1 = -‘ft^s-16t³ + I6t;

11.    a_n = ^{+ l}ft^s-16i³-J6ti

12.    @₂3 ⁼ ~    ^{777U 3+ 76U}'

13. n_zt/= + *tu^s- 16u³~ 76U)

@37 ⁼ @31 ⁼ ~ 41 /

15.    @33=    ⁼ - ^³>

16.    a„ = ~8i⁷+ 88i^s+№³-76(6-I/)t;

17.    Q_K = ~6i ^?- 681 ^r+ 96t³+76(6 - V)t;

18.    Q ь3 =~8u ⁷+48и*'+9би³-7£(ч~т7)и_}

19.    n_¥i=-8u⁷-68u*+98i/³-+76(4- \7)u;

20.

21.

22.

23. реиение система линейных уравнений относительно веиа-

вестнмх Cj lcir/'d); „    .    ,    —    ,    rr

⁷    ЩЬЩН^И, г

3) коэффициенты системи линейных уравнений для полубеоко-

15

35.    a_n~+ IB(2+ i/)t^v-Mi

36.    а„=+8и*-Щ1+2)Пи²)

37.    Дц = +16(2+l/)i/*- W)

Ч) вспомогательные величины для вычисления свободных членов системы линейных уравнений для полубесконечной трубы:

16

61.    определение свободных членов ;

4 -Д %' ^Ci ^0м2/Н ( = I. 2, 3, *);

62.    решение системы линейных уравнений относительно неизвестных Oj (см²/Н): Hdjjll-llC-Ihll^U; а = 7,4 , j=7,4);

5) вспомогательные величины для определения результатов вычислений:

63.    /}₂ =ch %_l-cds2_z i

6k. B_z =0,5(oh 2_Z sin Z_z + shZ_z cosZ_z);

65.    и_гт_г-ь-, 1

66.    uk^mTt + Viil

67.    ino) = (2 fa)'¹ (a_z r_z - u_zB_z)_} cm^z/H)

68.    Wty-MJl’rr'/z, CM*/Hi

69.    fijoj = JOOEh, id(o)/ R)

70.    щхдчао-ЕШХция i

71.    fi₂(o)=(M)(A_zV_z-B₂W_z), CM)

72.    d'-w*} d_t-w~*V; d_r/so²;d_s=t(h-u«)-,

73.    dp

7k. d_w = -<t[l2-(3+8V)t¹];

75.    d_v ~-8U^Z[6 + /(4-и *)J;

76.    d_n = -ь[12-(3+8\})и^г],

77.    u2(o)= d_BC_z + d₇C₃+d₃C_lf} см^г/н •

78.    М_г(о)-(В/оЩо^О_/0О_г^О„0₃ fd_nC,lcM;

79.    N_l[o)=~(mEkln)(t^l,c_l + jj

80.    Л^/V =(n/E^l)[(d_mVj t d^Cj H-d^td^cj

i(dj_z +d_n + (-(J₁₁V_Z + d_JZ1’_z)Ci_f]_} см-,

^8I* H2N=-№EA/W*V_rC_r + t*r₇C_t±v\£₃ t_U\ci

82. mo)=(d₆v^d_sT_l)c_Ji-(-d₅^td_er_i)G_l+_

HcfgVi +d₇T_z)C₃ + (-d₇V_z -r dgT^C^, см¹/н)

17

);

Mz(o) =[DlRz)[(dw V, + dg Щ+Нд Vj+d№Tj)Ct /

Мг1Л„/=11//л n*gb/T»„''ii~rt“3L'

83.

84.

85.

86.

3?.

88.

89.

90.

91.

92.    я

М₂д (о) = M^(o) + Mz(o) + M₂[o)i

to2д 1Хц)=^1^ц)+Щ&ц);

"глМ - Ш +%f⁰)+4°)j

'VV ^e

irlo)=    _f    Ш¹;

(,(*,) . mpd + Jk^,

DpiMUaii . Для даганейиих вычислений принимаем наибольшее as значений 6_Т , найденных в п.я. 91-92.    ¹

Выходная информация;

Н/см;

Ьттах

2. Qq ^ZlRIO'*^ «Ч ³-

4. допустимая начальная овальность (в %) согласно нормали [б] :    _

W[w(o)+ WfoJJMn

jj «    —    «г¹

“ н

4. РЕАЛИЗАЦИЯ РАСЧЕТОВ dA ЭВМ И РЕЗУЛЬТАТЫ ВАРИАНТНЫХ РАСЧЕТОВ

4.1. На основании приведенного алгоритма разработана программа расчета на ЭВМ ВС 10-22^х/ величины раажимной силы Q и допускаемой вмправляемой овальности у/ .

^ Программа расчета хранится в лаборатории математических методов исследований ВНИИСТа.

18

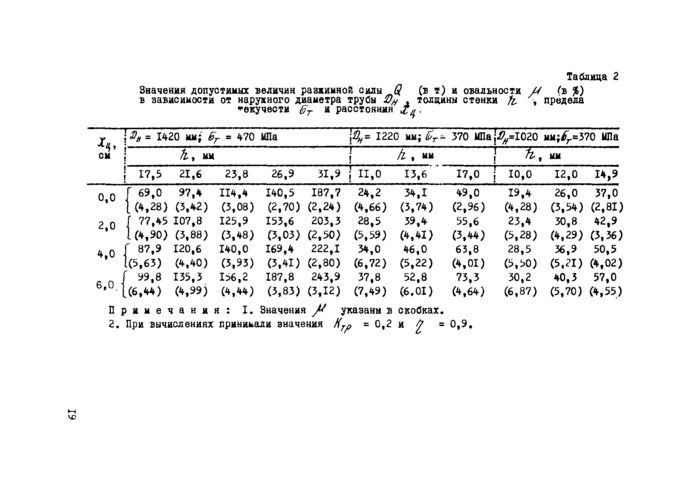
Таблица 2

Значения допустимых величин разжимной силы Q (в т) и овальности /4 (в %) в зависимости от наружного диаметра трубы щ , толщины стенки k предела текучести §_т и расстояния -

4.2.    Б результате расчетов на ЭВМ при различных исходных данных получен ряд наибольших допускаемых значений разжимной силы $ и овальности J4 , которые определены из условия, что фибровые напряжения не превысят нормативного предела текучести. Эти значения приведены в табл.2.

4.3.    Влияние коэффициента трения Кур на величину разжимной силы Q характеризуется данными для трубы О_н =

* 142 см ж Хц - 6 см, приведенными в табя.З.

Таблица 3

Значения разжимной силы S (в т) и допустимой овальности U (в %) в зависимости от толщины стенки it и коэффициента трения кур

Примечания; I. Значения//¹ -величины овальности указаны в скобках в %.

2. При вычислениях принимали £ = 0,9.

4.4.    Приближенный способ определения разжимного усилия и допустимой овальности для труб одного и того же диаметра приведен в приложении I рексывндуемои.Этот способ основав на анализе результатов вычислений по точной методике. Для пряиене -ния приближенного способа необходимо иметь значения разжимного усилия и допустимой овальности, определенных по точной методике для какого-то одного значения толщины стенки.

4.5.    Пример расчета разжимных усилий центратора и допустимой выправляемой овальности трубы (в соответствии с алго -ритмом расчета) приведен в приложении 2 справочном .

20

Министерство стро- !    Рекомендации    I    р дит    IftiT

ительства предпрн- jno расчету уоилий внутрен- ; яти* нефтяно* и {него центратора для оборки ;    “

газовой премиален- ;труб с начально* овальности; ^ ° ности    ;    сечений    ;

I. ОБЩЕ ПОЛОЖЕНИЯ

1.1.    Даннне Рекомендация дает возможность определять:

наибольшую допустямув овальность труб из уаловия, что

при их сборке материал труб работает только в упруго* области;

необходимую силу разжатия центрирующего ряда внутреннего центратора для втравленжя овальности.

1.2.    Разработка настоящих Рекомендаций внзвана необходимости проектирования внутренних центраторов для труб больного диаметра с учетом их начально* овальной*.

1.3.    Б Рекомендациях рассмотрев» оихм взаимодействия Дадду жамками одного центрирувщего ряда центратора и внутренне* поверхности труби с начально* овальности сеченн*.

1.4.    Настоящие Рекомендации равработанн с использованием положений, и вложен них в работе [I ], и результатов, получениях при рассмотрении напряженного состояния полубесконечно* цилиндрической оболочки, к которой щшдокенн оамоуравновеиеннне нагрузки, распределению вдоль вефикетри одного и того хе поперечного сечения [2], [з] . С&ноуравневеивннне позерхностнме нагрузки при сборже труб возникав* от действия центратора на внутреннее поверхность труби.

2. МЕТОДИКА РАСЧЕТА УСИЛИЙ ВНУТРЕННЕГО ЦЕНТРАТОРА ПРИ ВЫПРАВД&ИИ НАЧАЛЬНОЙ ОВАЛЬНОСТИ ТОРЦА ТРУБЫ

Основные допудения

2.1. Пряная груба (полубес конечная круговая цидиндриче-ская ободочка) инее* средний радиус сечения R и толциву стенки h (рис.1).

2.2. Деформации трубы обозначены в безразмерных продольной и угловой координатах = X)R, J5    (си.рис.I). Конпо -

К

невтм перемещения произвольной точки срединной поверхности труби по ннправлениям координат о( , [i и по нормали к срединной поверхности обозначена соответственно через LL _г , ^ и .

2.3. Труба имеет начальную овальность сечений, которую можно представить зависимостью

со

где (&а)_н ~ амплитудное значение начальных нормальных пе-' ремещений.

2.4.    Материал труби однородный изотропный и подчиняется закону Гука вплоть до достижения им предела текучести; алия*-нив двухосного напряженного состояния не учитываем.

2.5.    Сечение труби удовлетворяет условию тонкостенное» оболочек

2.6. Нормальные составляющие сил взаимодействия между центрирующим рядом и внутренней поверхностью трубы на всех стадиях нагружения принимаем непрерывно распределенными вдоль периметра производящей окружности по закону

+    (3)

где @ц - суммарное усилие жимков центрирующего рада;

2    -    коэффициент,    близкий    к    единице    (£    ^    I).

Плоскость, в которой действуют разжимные силы, отстоит от торца трубы на расстоянии Хц (см.рис.I).

2.7. В связи с тем, что перемещение жимков центратора происходит только в радиальном направлении, а точки средин -ной поверхности при выправлении овальности перемещаются как в радиальном, так и в касательном направлениях к средней линии сечения трубы, то между поверхностью жимков центрирующего ряда и поверхностью трубы, кроме нормальных усилий, возникают также силы трения Т , определяемые выражением

T-ffpjk^ataZfi,    <*>

где к_Тр - коэффициент трения.

5

В дальнейшем следует ограничиться только первым слагаемым формулы (5), так как изгиб по четвертой гармонике не реализуется в силу того, что начальная овальность описывается выражением (I), а жимхи всегда располагается по поверхности кругового цилиндра и поэтому:

(6)

2.8.    Ширину жимков (размер вдоль оси трубя) центрирующс-го ряха принимаем мало! по сравнение с размерами трубы, что позволяет исключить ив рассмотрения распределение усиди! вдоль оси труби.

2.9.    Принимаем в расчетах, что постоянная (кольцевая) и косинусоидальная составляющие нормальных сил взаимно не влияет на вызываемые ими напряженно-деформированные состояния трубы, и в расчете их воздействия суммируем. Такое допущение вытекает из предположения, что в конечно! стадии нагружения поперечное сечение трубы, совпадающее с плоскостью центрирующего ряда, не имеет овальности.

О теории расчета пидиндпичвокит пйпдпчйк на самоуравновеиенную нагрузку

2.10. Всякую произвольную самоуравновененную нормальную нагрузку Z(ji) , приложенную к поверхности цилиндрической круговой оболочки, можно представить в виде ряда элементарных

2.II. Исходя из рассмотрения условий равновесия элемента оболочки Rc/cit-Rdfi и условий совместности деформаций, в работе [i] показано, что реиение задачи о расчете цилиндрической оболочки кругового очертания, нагруженной нормальной поверхностной нагрузкой 2 _п , сводится к одному разрежающему дифференциальному уравнению, которое имеет вид:

6

^гдв t=nV(/7*-7)/2a)    u=\fa/2    -,    ~f~~ '

2.14. Функция <Р(<х) в (II) о учетом (14) для беоконвч -во! оболочки принимает вид:

(р=pfa)^+С_гТ(Ы)+С₃1Г(ш)+с# Т(и<х)+<р* _а5) где

VU^’sinfkTO^'cosO _ затухающее функции; Ч>^кй^м(2_п)₀Ш*(и^г~1)^гД - частное решение уравнения (12); и/ (j ~7,2,1,4] ~ произвольные постоянные.

Подставив внраженяе (15) в формула (9) и суммируя члени при аатухашра функциях, пожучим для всех составлявших лере-мещени! и внутренних сил в щиживдрнческо1 оболочке от нагрузки, распределенной по вакону В_п(В) =$_п )#. Cosfi,    одинако -

вие по структуре соотношения [2,3j :

H’t_H{c,[K„v(t<)+i₂„ пы]+с_г[-к_г11щ_л) *

+    rfoctj]*    (И,

+    Р(м)+ЬзнТ(иа]]+%м<р*}Т_п(р),

где Н - условное обозначение лвбаго из компонентов, пере-мешенш!, внутренних сил к моментов;

Zu,kj_u(HtM коэффициент, вираженвя для вычисления которых при 77 = 2, приведен и в табл.1;

тригонометрическая функция, принимаемая также ' согласно табл.1.

9