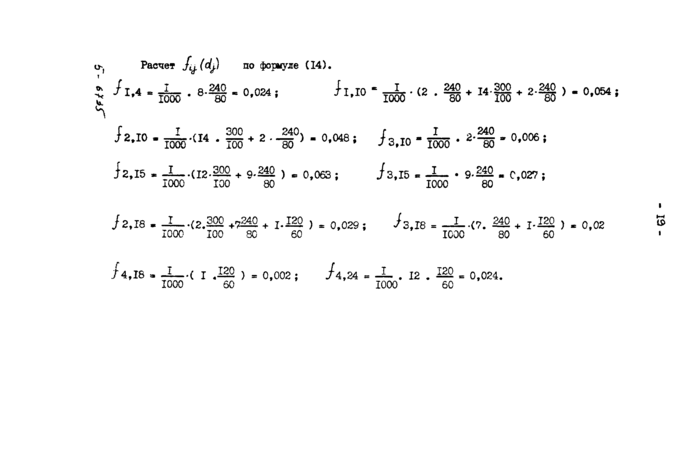ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ СОВЕТА МИНИСТРОВ СССР

ВСЕСОЮЗНЫЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ им. Д. И. МЕНДЕЛЕЕВА (ВНИИМ]

МЕТОДИКА

ОПРЕДЕЛЕНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК КОНТРОЛЬНО-СОРТИРОВОЧНЫХ АВТОМАТОВ МИ 126—77

МОСКВА — 19Г8

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ СОВЕТА МИНИСТРОВ СССР

Всесоюзный ордена Трудового Красного Знамени научио-м -следовательский институт метрологии иы.Д.И.Менделеева

(В Н И И Ы)

М Е ТО Д И К А

ОПРЕДЕЛЕНИИ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК КОНТРОЛЬНО-СОРТИРОВОЧНЫХ АВТОМАТОВ

МИ 126-77

Издательство стандартов

Москва - 197£

-10-

A A*2* Данные, полученные при испытании КСА вторым способом с помощью АПД типа I, вводят в ЭВМ для обработки по программе Р 2 в следующем порядке2 /г, Нр, М_0} А/₀, б_н} 6<р. _}&₀    (см.лер-

вый способ - п.4ЛЛ) ;

Г    - середина    t-rо    номинального интервала сортировки

Мен + М(Ы)н ,

_ _ ^

РЛЪП.] - см.первый способ - п.4.1.1 ;

P_£[l:rtJ - см.формулу (12) ;

^[1:В00] - см.первый способ - п.4ЛЛ ;

^2[12 800] - то же ;

- то же.

4Л.З. Данные, полученные при испытании КСА первым способом с помощью АПД, типа П, вводят в ЭВМ для обработки по программе Р 3 в следующем порядке:

см.первый способ - п.4ЛЛ ; dt - количество аргументов и значений табличной функции плотности измеренных размеров ; ли - см.первый способ - п.4.1.1 ;

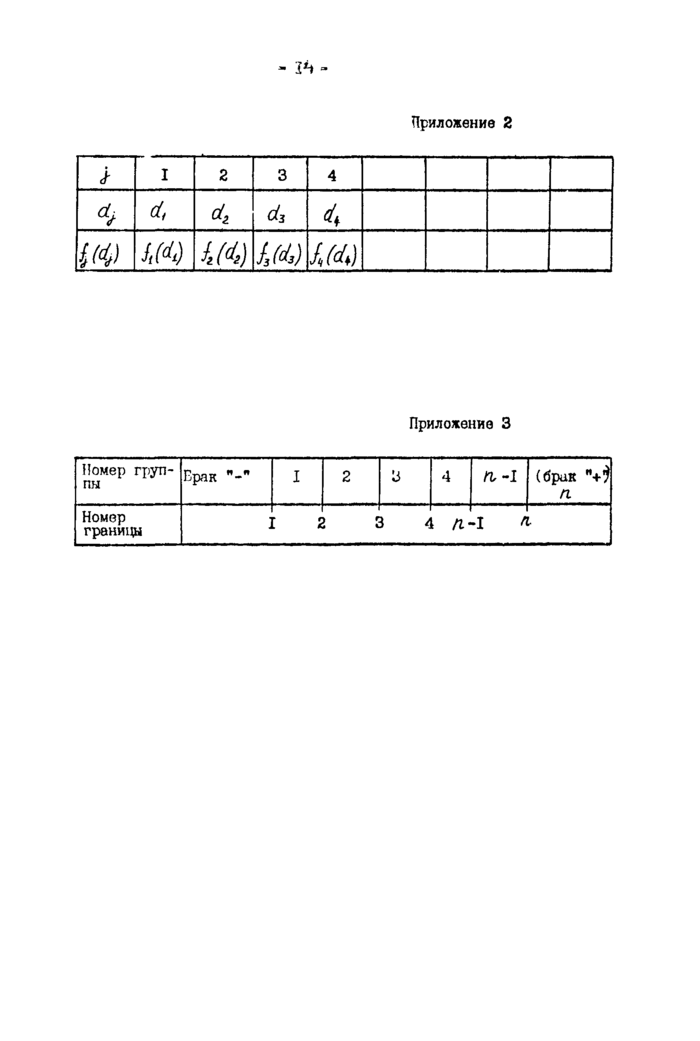
HIM]- таблица аргументов и соответствующих им значений функции плотности измеренных размеров (приложение 2) ;

-    см.первый способ - п.4.1.1 ,

-    количество аргументов для таблицы функции плотности

для i~й границы ( 6* I,    ;

SifrtOO]- см.первый способ - п.4ЛЛ ;

Ptlln] - то же ;

- L -я таблица аргументов

(t - I_f ..., Л ) и соответствующих значений функции (приложение б).

АЛ* Данные, полученные после обработки на ЭВМ:    *

Приложение I

ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ РАЗМЕРОВ В АЛД С ПОМОЩЬЮ СОСТАВНОГО КРИТЕРИЯ ДЛЯ МАЛЫХ ВЫБОРОК

Методика проверки нормальности, распределения результатов наблюдений приведена в справочном приложении I ГОСТ 8.207-76.

При проверке по критерию I вычисляют отношения d :

го

d =

где Xi - размер L-й детали ;

М - среднее арифметическое значение размеров 20 деталей ; смещенная оценка среднего квадратического отклонения, вичисляемая по формуле

сч

Если d не попадает в область допустимых значений 0,7290-0,8791 то гипотезу о нормальности распределения отвергают. Если попадает, то продолжают проверку по критерию П.

Для втого вычисляют оценку среднего квадратического отклонения по формуле

Если не более юднсй разности {%l~ М ) превышает значение 2,33 tS то гипотезу о нормальности распределения размеров принимают с уропнсу значимости 0,1, В противном случае гипотезу отвергают.

13-

Программа и контрольный просчет

1    ‘BEGIN*‘INTEGER*I,J;

2    'REAL*M,D,S,SS;

3    *ARRAY*Х[1:2 0 3 *

4    Р0042(Х);Р1041(Х);

5    M:=SS:=0;

6    'FOR*I:=l‘STEP*l‘UNTIL*20*DO*

7    Ы:=Ш-Х[1];

8    М:=М/20;

9    *for*i:=i‘step*i'untii.*20‘do*

10    SS: =SS+ (Х[ 1 ]-М) 12;

11    D:=SS/2 0;

12    S:=SQRT(D);

13    D: = 0;

14    ‘FOR'I: = l‘STEP*l‘UNTII<*20‘DO*

15    D: =D+ABS (X[ I ]-M);

16    D:=D/2 0/S;

17    ‘IF’D<0.729^VB^>0.8791‘THEN*

18    ‘BEGIN*P016>(1,'//////ГИПОТЕЗА О НОРМАЛЬНОСТИ

19    РАСПРЕДЕЛЕНИЯ ОТВЕРГАЕТСЯ/Ax* );

20    ‘GO ТО*‘К‘END*;

21    SS:=SQRT(SS/18);

22    J:=0;D:=2.33xSS;

23    ‘FOR*I:    ‘STEP*    1    *UNTIL*2    0‘DO*

24    ‘BEGIN*‘IF*(X[I]-M)«D‘THEN*J:=J+1‘END*;

25    ‘IF'J'HE МЕНЬШЕ*10‘THEN*P0165(1,‘//////ГИПОТЕЗА О НОРМАЛЬНОСТИ

26    РАСПРЕДЕЛЕНИЯ ПРИНИМАЕТСЯ/А* * );

?7 ‘ELSE*P0165(1,‘//////ГИПОТЕЗА О НОРМАЛЬНОСТИ

28    ОТВЕРГАЕТСЯ//хх*);

29    ‘К:‘END*;

3 *

- 15-

Приложение 4

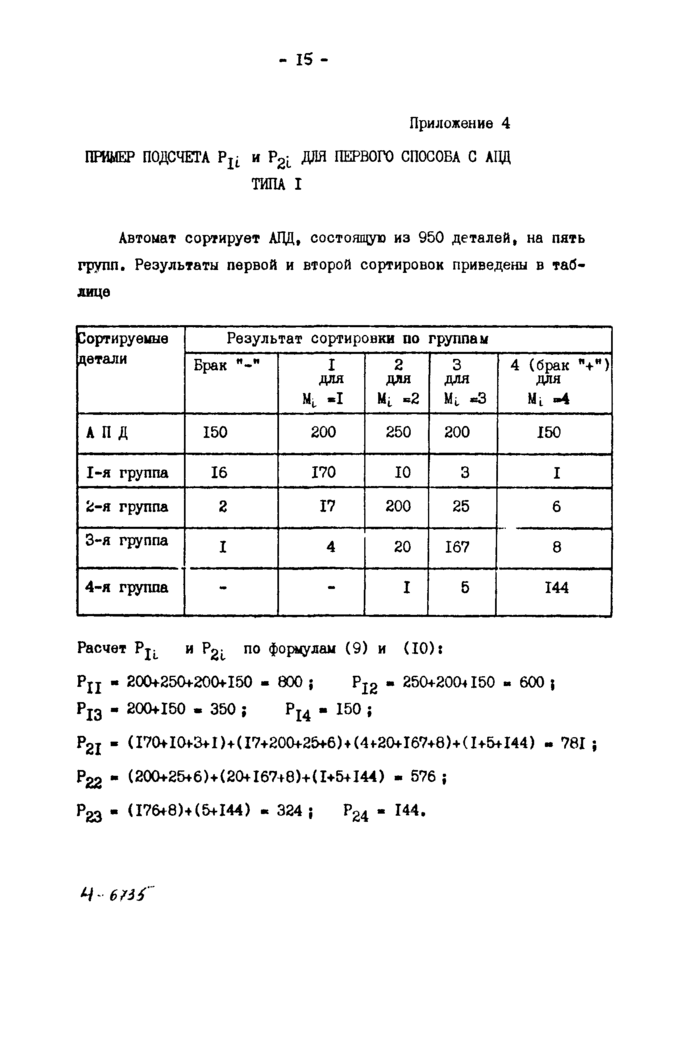
ПРИМЕР ПОДСЧЕТА Рц и Pg_L ДЛЯ ПЕРВОГО СПОСОБА С АПД ТИПА I

Автомат сортирует АПД, состоящую из 950 деталей, на пять групп. Результаты первой и второй сортировок приведены в таблице

Расчет Pj_L и Pg^ по формулам (9) и (10):

Р_п - 200+250+200+150 - 800 j Pj₂ - 250+200+150 - 600 j P_I3 - 200+150 - 350 ; Pj₄ - 150 ;

P_2I - (170+10+3+1)+(17+200+25+6)♦(4+20+167+8)+(I+5+I44) - 781 ; P22 - (200+25+6)+(20+I67+8)+(I+5+I44) - 576 ;

Pg3 - (176+8)+(5+144) - 324 i P₂₄ - 144.

4~ 6?if

Приложение 5

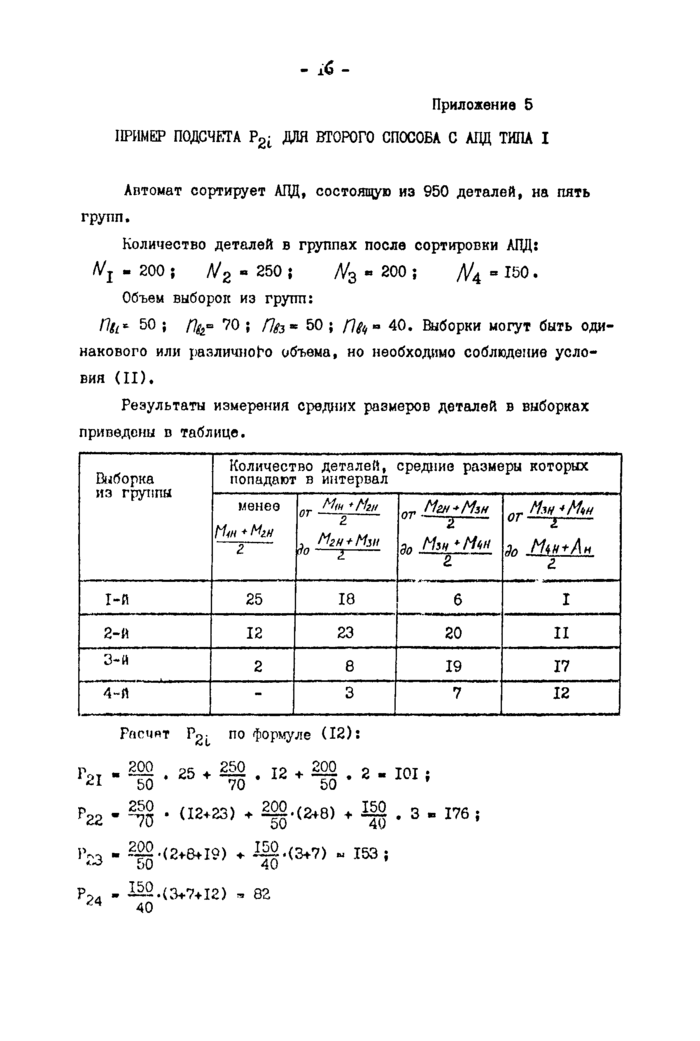
ПРИМЕР ПОДСЧЕТА ?_2l ДЛЯ ВТОРОГО СПОСОБА С АЛД ТИПА I

Автомат сортирует АЦЦ, состоящую из 950 деталей, на пять групп.

Количество деталей в группах после сортировки АЛД:

/Vj - 200 ;    Д/g    *> 250 ; /V₃ *» 200 ; /V4 = 150.

Объем выборок из групп:

П§[ * 50 ;    /7^0 70 ; /7^з* 50 ; /7^» 40. Выборки могут быть оди

накового или различного объема, но необходимо соблюдение условия (II).

Результаты измерения средних размеров деталей в выборках приведены в таблице.

Р₂₂ -    •    (12+23)    +    Щ-(ЬВ) + Ш

5V. -    -(2+6+19)    +    ~~-(3+7) ~ 153;

t>0    40

Р->, - —-(3+7+12) - 82 40

Приложение 6

ФУНКЦИИ ПЛОТНОСТИ ДЛЯ L -Й ГРАНИЦЫ

Приложение 7

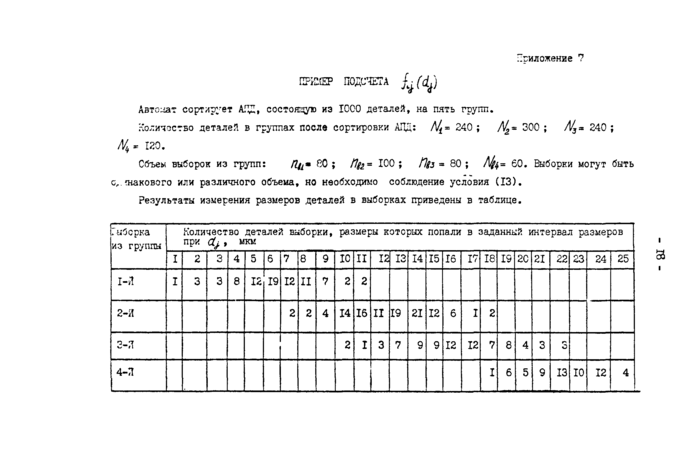
ПРИПЕР ПОДСЧЕТА £^(^)

Авто:^ат сортирует АП/;» состоящую из I0C0 деталей, на пять груш.

Количество деталей в группах после сортировки АЛД:    А*    =    240    ;    /]/^~    300    ;    А/₃=    240    ;

120.

Объем выборок из групп:    Ц^ш    80    ;    tlgt-    ЮО    ;    Пцз    =    80    ;    60.    Выборки    могут    быть

с,, знакового или различного объема, но необходимо соблюдение условия (13).

Результаты измерения размеров деталей в выборках приведены в таблице.

o-₍ Расчет    по формуле (14).

!

■ ik • ^e'^ ■ ^0,024' J¹-I0 * lofe • в • Ц ♦ И-88 - ²- °-⁰⁵⁴ >

•f ■ шг^сн • го *²' -i^0> ■ ^0,048!    ^.10 - ifeo • *ts' ^0,006 *

i2,I5 . -Z (12-202 + 9-240 j _{и 0} 003 .    J315 ₌ JL_ . 9-240 „ _{c 027} .

1000 100 80 1000 80

J 2,18 - -I--(2.200 ₊?240 ₊ j. 120 _{} ж} 0,029 ;    -/з,18    =    -Z--(7.    210    + 1-^22 ) , 0,02

1000 100 80 60 1000 80 60

/4,18 » -1--(    I    .122    )    =    0,002    ;    A,24    - -2- . 12 . 122 = 0,024.

1000 60 1000 60

РАЗРАБОТАНА Всесоюзным ордена Трудового Красного Знамени научно-исследовательским институтом метрологии им.Д.И.Менделеева (ВНИИМ)

Ю.В.Тарбеев В.М.Израилев В*М,Израилев А*С,Торопова В.Н.Горелик

ПОДГОТОВЛЕНА К УТВЕРВДЕНИЮ

Лабораторией законодательной метрологии ВНИИМ руководитель лаборатории М.Н.Селиванов Исполнитель    А.И,Орлова

УТВЕПЙДЕПА Президиумом научно-технического совета ВНИИМ 18 декабря 1976 г* (протокол № 8)

Приложение 8

АЛГОРИТМ, ПРОГРАММА И КОНТРОЛЬНЫЙ ПРОСЧЕТ ПО ПЕРВОМУ СПОСОБУ С АГЩ типа I

Определение значений Ml _и & сводится к решению систем нелинейных уравнений вида

fjk ₌т I М-Mi

/V« ^т° L \/б*+б?+б£

~    м₀*3б.

где % и /₀ - функции и плотность нормального распределения*

I• Ввод количества сортировочных групп И и признака .

2. Данные, полученные при испытании КСА первым способом, вводят в следующем порядке: /%,/у.ЛЛЛ. Р4[м],

ргуп), тшо],тщщ. _CM._n.4.i.i.

3* Печать заголовка*

4. Формирование граничных условий*

4*1* Для вычисления интеграла по СП р 0655: infl] - нижний предел интегрирования ;

(Л [2] - верхний предел интегрировангя ; in[З] - начальный шаг ;

Ш[4] - абсолютная погрешность вычисления интеграла.

4.2.    Для решения системы нелинейных уравнений по СП р 0651: еЛЩ- значения допускаемых погрешностей

SI, s 2 для уравнений системы ;

£$[3]| начальные приращения для аргументов

еЛии AXj; д х₂.

4.3.    Для отыскания корня функции на конечном отрезке по СП Р 10С\1:

dll] - начало отрезка ;

-3-

УДК 531.7:621.9.08(083.74)

МЕТОДИКА ОИРВДЕЯЕНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК КОНТРОЛЬНО-СОРТИРОВОЧНЫХ АВТОМАТОВ МИ 126-77

Настоящая методика распространяется на контрольно-сортировочные автоматы (КиА), сортирующие детали по линейным размерам, и устанавливает методы и средства определения метрологических характеристик раздельно по видам контролируемых размеров.

I. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

1.1.    К метрологическим .характеристикам относятся: интервал сортировки А ;

погрешность границ интервалов сортировки A U_L ; среднее квадратическое отклонение погрешности срабатывания на границах интервалов сортировки б- •

раэноразмерность деталей в сортировочной группе R^ ; смещение границ интервалов сортировки •

2. ВЫБОР И АТТЕСТАЦИЯ СРЕДСТВ, Г1РИМЕНЯЕМЫХ ДЛЯ ОПРЕДЕЛЕНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК

2.1.    Для определения метрологических характеристик КСА прима-няют аттестованную партию деталей (АЛД). Детали выбирают из числа тех, которые рассортировываются на КСА* Количество деталей

в АПД выбирают таким, чтобы после сортировки на КСА количество деталей No в каждой группе определялось условием

Ш

Он

З'де    -    номинальное    значение    интервала    сортировки    ;

б_н - нормированное значение среднего квадратического отклонения погрешности срабатывания. Значение б_н определяют из пас-

(Cj Издательство стандартов, 1977.

- 5" -

измеряемый размер может меняться вследствие погрешности формы измеряемых поверхностей (например, измеряемый диаметр меняется вследствие некруглости детали в контролируемом сечении), то измерение размеров каждой детали из выборки объемом 20 деталей на образцовом универсальном приборе по схеме измерения, реализованной в KUA, осуществляют в 10 случайных положениях, Предел случайной погрешности образцового прибора, определенный с вероятностью не ниже 0,95, не более 1/2 6_И

2,4,3.2, Для кавдой детали определяют средний размер по формуле    <°

i-cu

10

где (tjti - размер и -й детали в нение формы в случайном направлении

мером в первом направлении и средним размером по формуле

dm.n d_ifi den *

Допускается любое соотношение между отклонением формы детали и интервалом сортировки,

2.4,3.3, Нормальность распределения d_0n и d<p.n в АПД проверяют так же, как и в п,2.4.2.2. Если распределение don и d^n принадлежит нормальному, то относят АПД к типу 1, добирают выборку до 100 деталей, измеряют средние размеры этих деталей и определяют математическое ожидание и дисперсию dm по формулам (2) и (3), а дисперсию d<p,n по формуле    20_

,    dmfl

n*i

Если распределение dan и d<p.a в АПД не принадлежит нормальному, то относят АПД к типу П и добирают выборку до 400 деталей.

2.5. Аттестацию АПД типа П проводят следующим образом*

2,5.1. Применяют случайную выборку из АПД об i, сигм не

400 деталей. Если число деталей в АГЩ, выбранное в соответствии с условием (I), меньше 400, то объем выборки равен числу деталей а АЛД,

2.5.2,    Измеряют на образцовом универсальном приборе по схеме измерения, реализованной в КСА, размеры деталей выборки, В ситуации, рассмотренной в п.2.4.3,1, измерение производят в одном случайном положении (детали). Предел случайной погрешности образцового прибора не более 1/2 б_{н 9} минимальная дискретность отсчета по прибору - не более б_{н щ}

2.5.3.    По результатам измерений строят табличную функцию плотности измеренных размеров (приложение 2). Для зтого весь диапазон измеренных размеров от ^ до (Umax ^4 min и сЦ max ~ наименьший и наибольший результат измерения деталей выборки) разбивают на интервалы, приблизительно равные б_н . Середины интервалов dj. являются значениями аргумента. Разность между соседними значениями аргумента определяется формулой

Ad- dj. * б_{и 9}    (7)

где J. * 1,2,3,....

Значения функции плотности для d^ подсчитывают по фор|*уле

<»

где tij - количество наблюдений, попавших в интервал

dj * ^d.H ^    .

2 ’ 2. >

Л£- количество деталей в выборке.

3. ОПРЕДЕЛЕНИЕ 'МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТШС

3.1* Первый способ определения метрологических характеристик КСА с помощью АЛД типа I рекомендуется для исследовательских метрологических работ и представляет собой с л едущее.

3.1.1.    АЛД сортируют на КСА на группы.

3.1.2.    Го тем пересчета или взвешивания определяют количество

- 7-

деталей в каждой группе*

3.1.3.    Подсчитывают для каждой границы Mi количество деталей Рй , размеры которых признаны автоматом в результате первой сортировки больше Mi , по формуле

Ря-i. Щ    М    -.*’    (9)

Л/

где /у - количество деталей в ^ -й сортировочной группе.

Соответствие нумерации границ и групп приведено в приложении 3.

3.1.4.    Все сортировочные бункеры очищают.

3.1.5.    Детали каждой сортировочной группы вновь сортируют раздельно на КСА.

3.1.6.    Путем пересчета или взвешивания определяют количество деталей, оставшихся в сортировочной группе и перешедших в результате сортировки в другие сортировочные группы.

3.1.7.    Подсчитывают для каждо/i границы Ml количество деталей Psi , размеры которых признаны автоматом в результате первой и второй сортировок больше Mi по формуле

А/

где riji - количество деталей, оставшихся в j. -й сортировочной группе после второй сортировки ;

^ - количество деталей, перешедших в результате повторной сортировки из i-й и с большими номерами (большими размерами) групп в j -ю группу.

Пример подсчета /* и Р& приведен в приложении 4.

3.1.8.    Для определения A ti повторяют через заданный интервал времени операции 3.I.I - 3.1.3.

3,2. Второй способ определения характеристик К*;А о помощью АИД типа I рекомендуется для испытаний а производственных условиях (здесь требуется одна сортировка АИД на группы).

- 8 -

3.2.1.    Проводят операции» приведенные в пп.3.1Л ; 3.1.2 ; ЗЛ.З.

3*2.2, Осуществляют случайную выборку из каждой сортировочной группы. Объем каждой выборки flgc определяется формулой

■    (И)

3.2.3.    Измеряют размеры каждой детали в выборках по п.2.4,3Л и определяют средний размер по формуле (4).

3.2.4.    Подсчитывают для каждой границы Mi количество деталей P₂i , средние размеры которых меньше ~^iH^

в t-й и группах с большими номерами» по формуле

⁽¹²⁾

Пример подсчета r_zi приведен в приложении 5.

3.2.5.    Для определения nil повторяют через задан -ный интервал времени операции 3.I.I. - ЗЛ.З.

3.3. Способ определения характеристик КСА с помощью АЛД типа П рекомендуется для испытаний в производственных условиях (здесь требуется одна сортировка АЛД на группы).

3.3.1.    Проводят операции» приведенные в пп.3*1.1., 3.1.2, ЗЛ.З.

3.3.2.    Осуществляют случайную выборку из каждой сортировочной группы. Объем каждой выборки fLfc определяется формулой

(13)

3.3.3.    Измеряют размеры каждой детали в выборках по п.2.5.2,

3.3.4.    По результатам измерений для каждой границы строят табличные Функции плотности распределения измеренных размеров (приложение 6).

Разность между соседними значениями аргумента определяется

- 9 -

формулой (7). Значения плотности для Д подсчитывают по формуле    J^>п-    .

ч    (14)

„    di    f    at,

где tijj) - количество размеров, попавших в интервал

~    ~ ^В    v    с    большими    номерами сортировочных группах.

Пример подсчета    приведен    в    приложении 7.

3.3.5. Для определения Л ti повторяют через заданный интервал времени операции 3.1.I - 3.1.3.

4. ОБРАБОТКА РЕЗУЛЬТАТОВ

4.1.    Данные, полученные в разделах 2 и 3, вводят в ЭВМ для обработки по программам, приведенным в приложении 8.

4.1.1.    Данные, полученные при испытании КСА первым способом с помощью АЛД типа I, вводят в ЭВМ для обработки по программе

IP I в следующем порядке;

ft - количество сортировочных групп ;

^г{ - для пересчета Ми ( i - I, . . . ,/z ) - значений границ интервалов сортировки через определенный интервал времени ;

О - без пересчета Ми ;

М₀ - см.формулу (2) ; N₀ ; б_н ; 6<р,    -    см.формулу (6) ;

Gq - см.формулу (3) ; Pj [i :п] - см.формулу (9) ; Р₂ [i in] -- см.формулу (10) ;

Si [l:800j    - таблица значений функции плотности для нормального

закона (сы.Веитцель Е.С. "Теория вероятностей",

М., "Наука", 1969 - приложение 3) ;

S^psBOOj - таблица значений функции интеграла вероятности для нормального закона ;

- значения Pj [l: tl] ₉ определенные через интервал времени t (вводится при Up ■ I) по пи.3.1.8;

3.2.5 ; 3.3.6.