етодические рекомендации по расчету плоской (профильной) установившейся фильтрации
Белгород 1979
МИНИСТЕРСТВО ЧЕРНОЙ МЕТАЛЛУРГИИ СССР СОЮЗРУДА
Всесоюзный научно-исследовательский и проектно-конструкторский институт по осушению месторождений полезных ископаемых,специальным горным работам,рудничной геологии и маркшейдерскому деду
В И О Г Е М
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РАСЧЕТУ ПЛОСКОЙ (ПРОФИЛЬНОЙ) УСТАНОВИВШЕЙСЯ ФИЛЬТРАЦИИ
Белгород
На рис.2 точки 4,5; 1,2 - отрезки кон
|
5,6 - части флютбета, 4,5,10,9 - шпунт, представлен как зона неоднородности с коэффициентом фильтрации 'Кф = 0; |
|
//ом.ео(2 JOM |
тура, где приложен напор; 2,3; 3,4 - кри -вая депрессии.
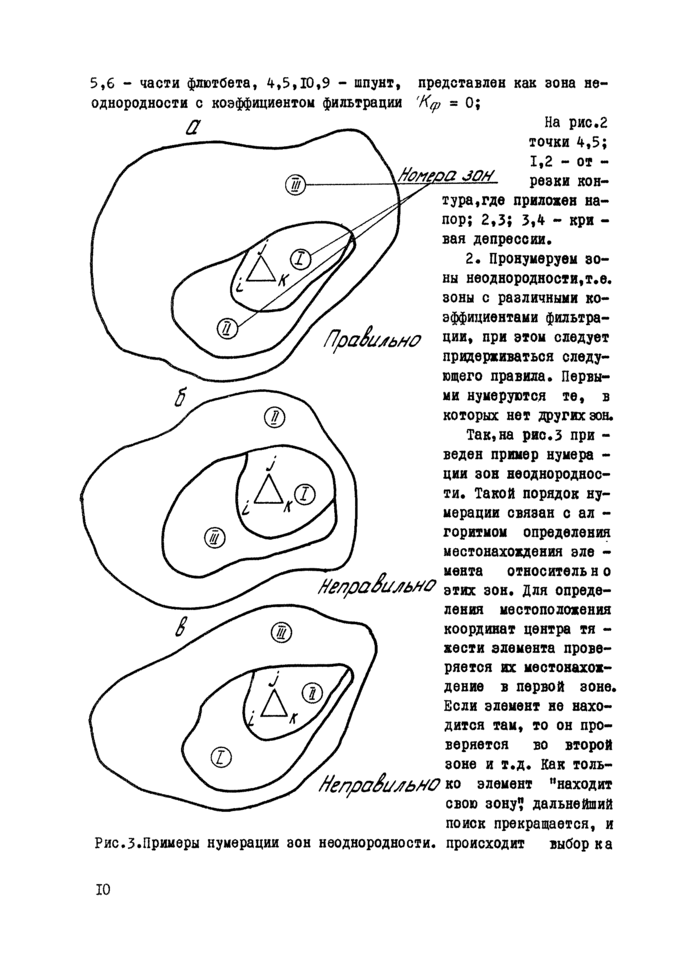
2. Пронумеруем зоны неоднородности,т.е. 80ны с различными коэффициентами фильтрации, при этом следует придерживаться следующего правила. Первыми нумеруются те, в которых нет других зон.
Так,на рис.З при -веден пример нумера -ции зон неоднородности. Такой порядок нумерации связан с ал -горитмом определения местонахождения эле -* мента относитель н о
f/£/7pQOL/JbM0 этих зон. Для определения местоположения координат центра тя -жести элемента проверяется их местонахождение в первой зоне. Бели элемент не находится там, то он проверяется во второй зоне и т.д. Как толь-МепраЗилбМ КО элемент ’’находит свою зону? дальнейший поиск прекращается, и
Рис.З.Примеры нумерации зон неоднородности, происходит выбор ка
коэффициентов фильтрации из массива МПI. Так, элемент (*V^) Для программы в случаях а, б и в находится в первой зоне,так как его местонахождение проверяется сначала относительно первой эоны (см, рис.з). Вторая зона сама находится в первой, поэтому и элемент, лежащий в ней, тоже будет для программы находиться в первой зоне.
2.4. Подготовка числовой информации для ЭВМ
1. Определяем К„, Кх . На выбор Ах накладываются следующие условия: I) (Л^.+ 1)^500, ИлГ^ЗО. С учетом значе -
ний К и % Ах в расчетной области происходит (при работе програм -мы) выборка наибольшей ординаты faca и абсциссы По этим
КООрДИНатаМ СТРОИТСЯ ПРЯМОУГОЛЬНИК СО СТОрОНаМИ
который разбивается на Ау полос по вертикали и Ах полос по гори -зонтали, т.е. на ( АуАх ) прямоугольных элементов со сторонами а• } S- , которые в свою очередь разбиваются на
два прямоугольных треугольника - основные элементы сетки. В принципе, чем гуще разбивка, т.е. чем больше А у и Ах% тем точнее результат счета. Для простых областей при ограничении машинного времени можно количество элементов уменьшить, но тогда величина элемента увеличится, что приводит к более приближенному описанию зон неоднородности.
2. I - число, равное количеству зон неоднородности, так, для расчетной схемы рис Л 7= 2, для расчетной схемы рис.2 7=1.
3.71 - число, равное количеству чисел в массиве/ШУ/, опре -деляется после того, как сформирован массив МХУ! •
Так, например, в расчетной схеме рис.1, прил.1 массив имеет 2О чисел, 71 =£0.
число, равное количеству чисел в массиве ГР, так, например, в расчетной схеме(см.рис.1,прил.1) массив имеет 36 чисел, Ed: 36.
5. После того, как были пронумерованы зоны неоднородности и их характерные точки, описывающие данные зоны, формируется массив
МХУ7-.
а) в порядке нумерации зон по характерным точкам обходятся зоны неоднородности. Обход может осуществляться как по часовой, так и против часовой стрелки, но выбранное направление обязательно сохранять для описываемой зоны.
Для тестовой задачи (см.рис.1, прил.1) зоны можно обойти по следующему маршруту: I зона - 9,4,5,10,9; П зона - 1,2,7,8,1. При
II
этом обязательно замыкать зовы той хе точкой иэ которой вышли. Так, в нашем примере I вону замкнули 9-й точкой, П - 1-Й точкой;
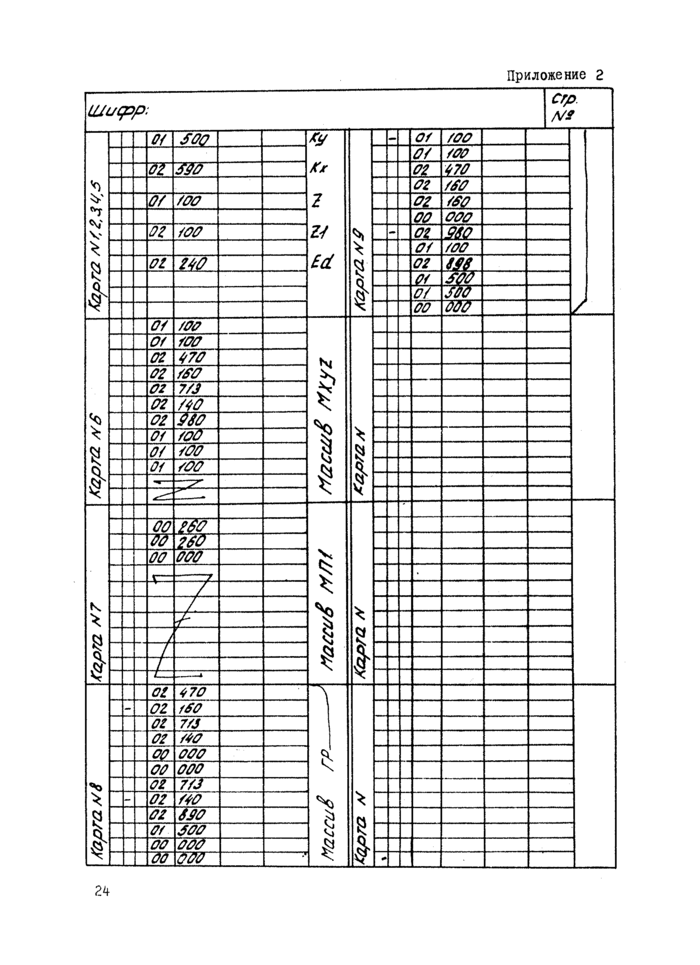
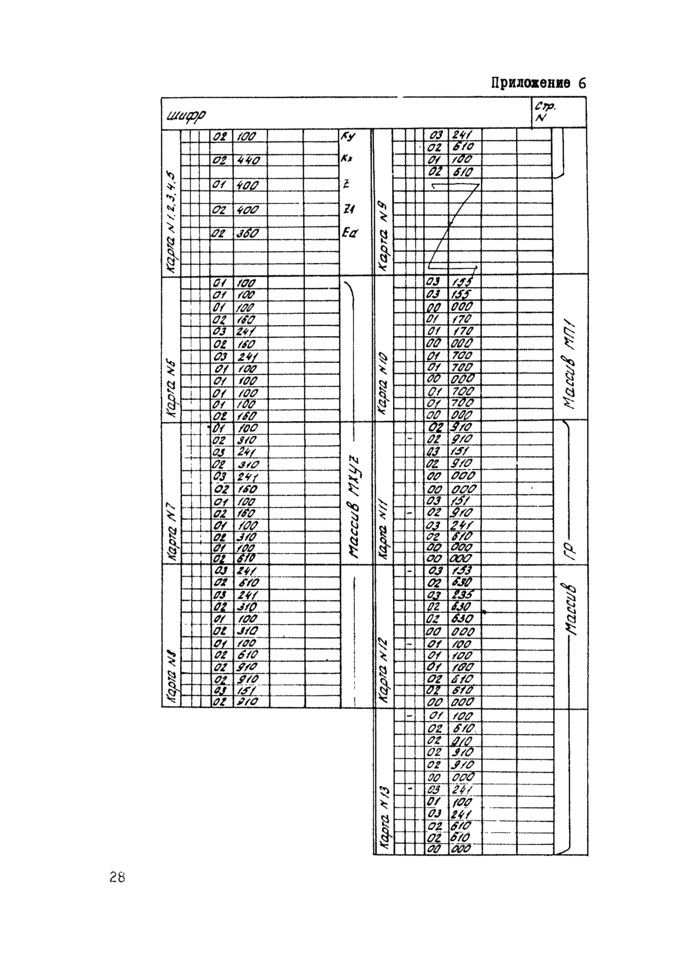
б) после того, как маршруты установлены, номера точек заменяются их координатами х% у % и это записывается на специальных бланках (см.риоЛ, прил.1; рис.2, прнл.2).
6. Массивом МИ задаютоя фильтрационные характеристики зотм неоднородности. В соответствии с нумерацией вон каждой присваивается три характеристики:
а) коэффициент фильтрации Кф по оси X ;
б) коэффициент фильтрации А'ф по оси^ ;
в) угол анизотропии (X в радианах;
Для изотропного грунта \• ОС * 0.
Если расчетная область состоит Из /г зон неоднородности, то фильтрационные характеристики записываются в следующем порядке на
'%'<*>'
в кружочках - номер зоны неоднородности (ом.приложения).
7. Массив ГР [I : ЕсП используется для задания граничных ус -ловий расчетной области и изменения первоначального регулярного деления области на окончательное.
Задание граничных условий производится по следующим правилам:
а) отрезки, на которых веданы равные расходы или равные напоры, нумеруются в произвольном порядке;
б) в порядке нумерации на отрезках записываются условия по фор-
“е о/н о ,
12 3^56
где j- координаты концов отрезка; i- номер точки одного конца отрезка; у- номер точки второго конца отревка; знак ♦ пе -ред СГ.; означат, что задан расход; знак - перед &£ означает, что задан напор; пятое число - значение расхода или напора, шестое число 0;
в) точка с граничными условиями рассматривается как отрезок с нулевой длиной и записывается так, как указано в п. б • В атом случае Х£Ц- XjU;.
Для простого смещения узлов запись отрезка, на котором должны находиться узлы, производится аналогично указанной в п. б , только знаки при X и и - положительные, а пятое и шестое числа всегда равны 0.
Любой отрезок массива ГР с краевыми условиями иди для простого омецения является местоположением ближайших к нему узлов.
С помощью массива ГР можно так описывать зоин неоднородности, чтобы на сторонах лежали узловые сетки. Этот прием был нспольво -ван я в тестовой задаче (см.рнс.1, прил.1), где в массиве ГРСУл описан шпунт.
В атом случае смещается ближайший к описываемому отрезку увел, о чем всегда надо помнить, т.е. увел, у которого расстояние по горизонтали до описываемого отревка -= 0,5В или по вертива л и -«=0,5/?, где в , fl - величины соответственно элемента по осям
Хл и ;
г) внак - перед координатой^- означает, что данный отрезок (точка) принадлежит кривой депрессии (см.рис.2, прил.2). При этом вначале лучше задать кривую депрессии, а потом другие гра -вичные условия. В напорных задачах, где нет кривой депрессии, условия кривой депрессии не задаются(ом.рнс.1,прил.1;рнс.2,прил.2).
3. ПРИМЕРЫ РЕШЕНИЯ ПЛОСКИХ ПРОФИЛЬНЫХ ЗАДАЧ ФИЛЬТРАЦИИ
|
ЭГДА, которые |
|
Рис.4. Расчетная схема фильтрации через основан и е бетонной плотины со шпунтом:
— о — - аналити -ческое решение ; | |
По данной программе был решен ряд задач (часть не них приведена в настоящих рекомендациях^ для контроля результаты расчетов на ЭВМ были сравнены с результатами расчетов методом проводились Харьковским отделением ВОДГЕО. Задачи 5,6,7 были решены только с помощью программы с целью определения гра -
-«-решение МКЭ. _f -0.75-0.5-0.25
ниц применения данной программы к решению аналогичных задач. Решение фильтрационной задачи по программе в сравнении о точиш аналитическим решением приведено на рис.4.
Задачи, приведенные в настоящей работе можно привести к пяти типам:
1. Фильтрация черев основание бетонной плотины оо шпунтом Сз].
2. Фильтрация в земляной плотине с каменно-набросной дренажной приэмой.
3. Фильтрация через земляную плотину с экраном.
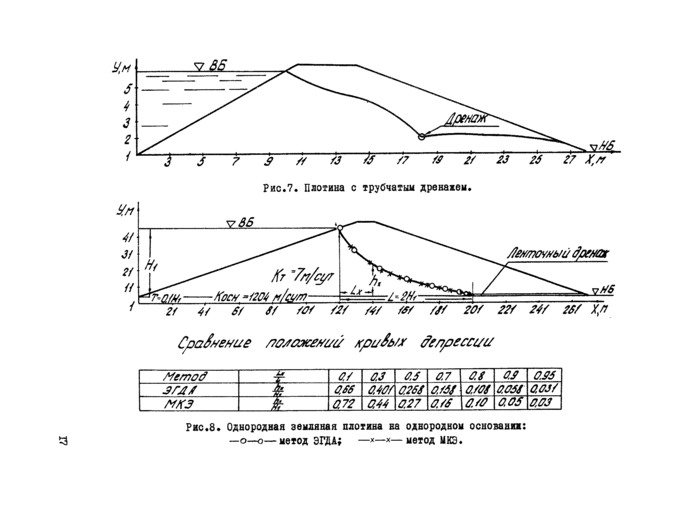
4. фильтрация черев земляную плотину с трубчатым дренажем.
5. Фильтрация в земляной плотине с ленточным дренажем.
Рассмотрим подробнее подготовку исходных данных для приведен -
ных и аналогичных фильтрационных вадач.
3.1. фильтрация черев основание бетонной плотины со шпунтом, напорная фильтрация
В этом типе задач благодаря тому, что все краевые условия из -вестны, решение происходит за один цикл (в понятие "цикл" входит формирование и решение системы уравнений). Расчетные области задач такого типа могут иметь практически любую геометрию, сам ы е причудливые зоны неоднородности с различными коэффициентами фильтрации. Так, на рис.4 приведена расчетная схема фильтрации черев основание бетонной плотины со шпунтом. Задача была решена при >£ = 0 и ^=0,5, где 5-длина шпунта, м; Т- мощность подстилающего слоя, м; лежащего на водонепроницаемом основании. Шпунт был представлен как зона неоднородности с коэффицие н т о и фильтрации К$жК0 и 0, где As- коэффициент фильтра ци и шпунта; К0~ коэффициент фильтрации подстилающего сдоя (си.прил.1 к рис.1). Расхождение с точным аналитическим решением менее 1%).
3.2. фильтрация в земляной плотине с каменнонабросной призмой
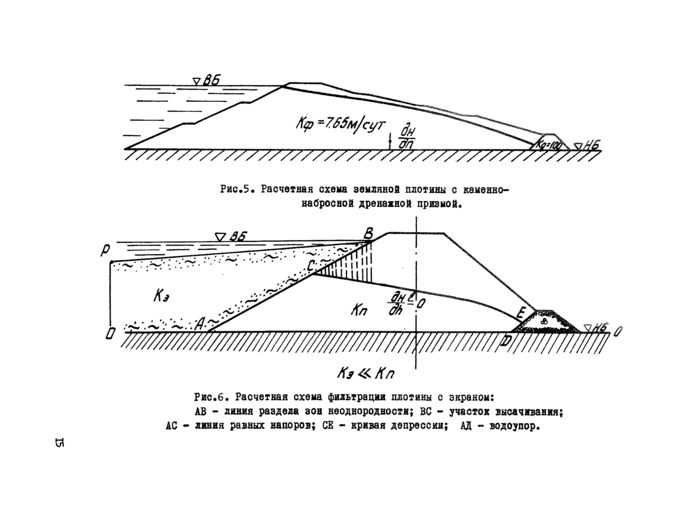
В задачах такого типа каменная наброска ведается как зона не -однородности с большим коэффициентом фильтрации. Подученные решения позволяют сделать вывод о том, что при коэффициенте фильтра -ции призмы НПр более 1,5 (Кп- коэффициент фильтрации плоти -ны) влияние призмы на положение кривой депрессии в теле плотины не наблюдается (рис.5).
14
|
|
Рис.5. Расчетная схема земляной плотины с каменно-набросной дренажной призмой. |
|
|
штттщштмть
Рис.6. Расчетная схема фильтрации плотины с экраном:
АВ - линия раздела зов неоднородности; ВС - участок высачпанкя; АС - линия равных напоров; СЕ - кривая депрессии; АД - водоупор. |
Л> « Кп
УДК 626.001.2
В настоящих рекомендациях приводится методика, позволяющая решать плоские профильные задачи фильтрации при одновременном наличии анизотропии и неоднородности фильтрационных свойств. ко программе с автоматической раз -бивкой области, использу;: индивидуальный подход, можно решать практически все инженерные задачи.
Рекомендации могут быть использованы специалистами, работающими в области исследования и проектирования гидротехнических сооружений.
работа выполнена в лаборатории устойчивости хвосто -хранилищ гидротехнического отдела ВИОГЕМ канд.техн. наук С.Г.Аксеновым, инженерами В.И.Истоминым и О.Н.Полищук. В разработке методики принимали участие канд.техн. наук А.С.Смирнов, инженер А.Ф.Контримавичус. Утверждена сек -цией НТС института 22 февраля 1979 г. в качестве методических рекомендаций.
Все замечания просим направлять по адресу: 308007, Белгород, В.Хмельницкого, 86, институт ВИОГВМ.
V^/Всосокюный научно-исслеловатольскнЛ и проектно-конструкторский институт по осуишпию месторождений полезных ископаемых, специальным горным работам, рудничной геологии и маркшейдерскому делу ( ВИОГЕМ), 1970.
ВВЕДЕНИЕ
Современные обогатительные фабрики предприятий черной металлургии и других отраслей промышленности строят и эксплуатируют, так называемые, хвостохранилища,емкость которых иногда достигает 400 и более млн.м3, для складирования отходов обогащения и осветления воды с целью повторного ее использования в производственном цикле [I]. Лоха хвостохранилищ и ограждающие их сооружения практически всегда сложены водопроницаемыми грунтами. В связи с этим при про -актировании хвостохранилшц должны, как правило, выполняться фильтрационные расчеты, в результате которых в общем случае определяются следующие параметры фильтрационного потока: гидродинамические сетки фильтрации; градиенты напоров и скорости фильтрации; фильтрационные расходы (удельные и полные) для заданной об -ласти или ее части;
поверхность депрессии и участки высачивания для безнапорной фильтрации.
Хотя в большинстве случаев фильтрационный лоток на участке хвостохранилищ имеет пространственный характер, на достаточном удалении от него - плановый и только на отдельных участках ограждающих сооружений - плоский, во многих случаях удается путем достато ч я о обоснованной схематизации свести задачи двух первых видов к плос -кой задаче фильтрации.
Следует отметить, что плоская задача фильтрации решается наиболее часто при проектировании гидротехнических сооружений в гидро -энергетическом и мелиоративном строительстве.
За полувековую историю развития теории фильтрации в СССР и за рубежом разработано много методов решения задач плоской установившейся фильтрации как теоретических (точных и приближенных), так и экспериментальных [I]. С помощью их решены достаточно сложные задачи, имеющие народнохозяйственное значение. В то же время необходимо отметить известную ограниченность ранее разработанных метод о в решения плоской задачи фильтрации, которая состоит в следующем.
Теоретические методы решения ввиду несовершенства математичес -кого аппарата разработаны для узкого круга эадач, т.е. для частных случаев плоской эадачи фильтрации, экспериментальные же методы, с
3
одной стороны, сопряжены с трудностями технического порядка, особенно для сложных областей фильтрации, а с другой - недостаточно точны. Та и другая группа методов расчета не позволяет решать задачи фильтрации о учетом анизотропии и неоднородности фильтра -ционных свойств и практически применимы лишь для решения частных случаев анизотропии или неоднородности.
В связи с изложенным авторами разработана методика приближен -ного расчета плоской установившейся фильтрации с использова и и е м ЭВМ, по которой можно учитывать любую геометрию области, неодно -родность и анизотропию фильтрационных свойств при заданных гра -яичных условиях, в том числе с неизвестными границами.
В основу методики положена программа расчета плоской уста но -вившейся фильтрации, составленная в лаборатории устойчивости хво-стохранилищ гидротехнического отдела. Программа составлена на языке АЛГОЛ-60, ТА-2М! В качестве метода решения задач использован метод конечных элементов. В процессе работы над методикой решения плоских (профильных) задач фильтрации с применением ЭЦВМ были составлены программы с ручной и автоматической раз -бивкой на конечные элементы расчетной области. Эффективность программ была проверена на решении однотипных задач. При этом особое внимание было обращено на работу программ с областями, имеющими зоны неоднородности. Анализ результатов счета даже для самых сложных областей показал, что точность расчетов по обеим программам существенно не отличается. Так как подготовка исходных данных в программе с ручной разбивкой более трудоемка (примерно в 40 раз) по сравнению с программой с автоматической разбивкой, в дальнейшем велась работа над программой с автоматической разбивкой рас -четной области.
Авторы признательны главному специалисту ОМИРа В.А.Васильеву,а также начальнику гидрогеологического отдела Ю.И.Ляпину и руково -дителю группы того же отдела З.И.Письменецкой за предложения и замечания, сделанные ими в процессе подготовки работы к публика -ции. Авторы будут признательны организациям, использующим методику при расчете фильтрации, за замечания и предложения по улучше -ншо настоящих рекомендаций, а также за сообщения об объемах и результатах их внедрения. 1 2
I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДИКИ
В качестве расчетной физической модели принимается пористая недеформируемая среда, в которой происходит фильтрация кесхима -емой жидкости.
Принимая ось X горизонтальной и направляя ось у вертикально вверх в соответствии с законом Дарси, имеем следующие уравнения установившейся фильтрации:
где fl-jr* у ~ пьезометрический напор, м; Р- давление в жидко -сти, Т / м2; У - удельный вес жидкости, т/м3; у- расстояние от данной точки до плоскости сравнения, м; и /fy - коэффици
енты фильтрации для неоднородной анизотропной среды соответственно в направлении осей х и у , м/сут.
Уравнения, связывающие вектор скорости фильтрационного потока с пьезометрическим напором и коэффициентом фильтрации, не позволяют решать конкретные задачи, если неизвестно дифференциаль -ное уравнение в частных производных, записанных для области фильтрации с определенными граничными условиями. Такое уравнение по -дучают из закона неразрывности фильтрационного потока, с учетом закона Дарси оно преобразуется в линейное дифференциальное урав -нение в частных производных второго порядка Г27
Решение плоской установившейся фильтрации заключается в реше -нии уравнения при следующих граничных условиях:
на водопроницаемых границах, находящихся под уровнем воды, h равен пьезометрическому напору;
на водонепроницаемых участках производная по нормали к гра-ницв f=0;
на промежутке высачивания
на свободной поверхности и .
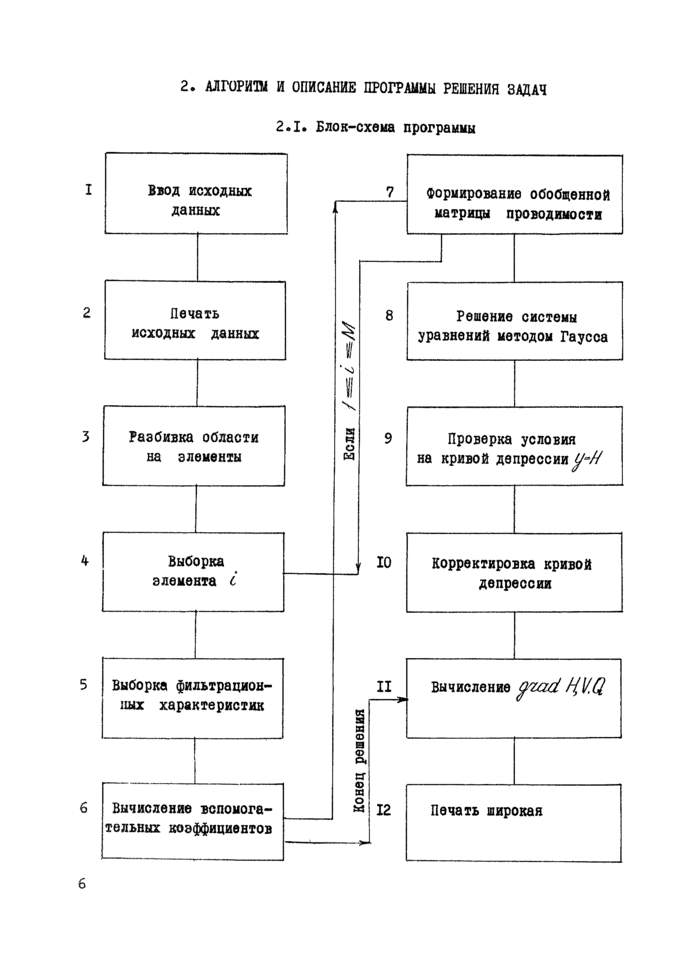
2. АЛГОРИТМ И ОПИСАНИЕ ПРОГРАММЫ РЕШЕНИЯ ЗАДАЧ
|
2*1. Блок-схема программы |
|
I
2
3
5
б | |
Выполняемые операция и действия
Описание простых переменных целого и вещественного ти -па. Описание массивов. Ввод исходных данных
Печать исходных данных 0U^ МХУ^МЩГР)
на узкую печать
Происходит разбивка расчетной области на прямоугольные треугольники согласно Кх и Ку Описание этих элементов по номерам уэлов, массив ИНФ. Деформация сетки согласно массиву ГР. Присвоение узлам граничных условий согласно массиву ГР
Согласно нумерации элементов происходит выборка номеров узлов С -го элемента, координат увлов для этого элемента
Согласно местоположению С-го элемента относительно вон неоднородностей происходит выборка фильтрациоиных ха -рактеристик
Вычисляются вспомогательные коэффициенты А, В
Вычисляются коэффициенты матрицы проводимости для С -го элемента, которые тут же заносятся в обобщенную матрицу проводимости
Решение системы производится методом Гаусса, т.е. мат -рица MG приводится к треугольному виду, затем обратным ходом определяются неиэвестные напоры
Проверка условия на кривой депрессии сводится к уста -новлению разности между напором Н на кривой депресс и и и координатой у узла, в котором берется напор
Корректировка координат сетки осуществляется в случав несовпадения //и (у /И
По известным узловым напорам происходит расчет градиентов напоров, скоростей VXt Vy , расходов Q
Печать конечных результатов, таблицы напоров, градиентов скоростей и расходов для каждого элемента
2.2. Подготовка исходной информации
1. Примерно, но заведомо выше своего вероятного положения на чертеже проводится кривая депрессии в виде ломаной линии. Все,что ниже кривой депрессии, называется расчетной областью. Вся работа в дальнейшем ведется с этой областью. При этом, чем ближе прове -дена начальная кривая депрессии к ее действительному положен и ю, тем быстрее решится задача.
2. Расчетная область фильтрации, включающая зоны неоднородности, описанные ломаными линиями, наносится на миллиметровку.
3. Привязка расчетной области к определенной системе коорди -нат производится в следующем порядке. На край расчетной области со отороны большего напора прикладывается ось у так, чтобы она проходила через самую крайнюю точку этой области. Осъх наклады -вается так, чтобы она проходила черев самую низкую точку области.
|
|
Рис.1. Расчетная схема напорной фильтрации под плоским флютбе-том со шпунтом: (I), (П) - зоны неоднородности. |
Направление оси у всегда вверх, направление оси X - от оси в сторону области. Точка пересечения координатных осей имеет коор -динаты X = I, у= I. Характерные точки расчетной области привязываем к принятой системе координат. Так, например, на рис.1 приведена расчетная схема фильтрации под плоским флютбетом со шпун -том. В этой схеме вся область - область фильтрации, поэтому весь контур 1,2,7,8,1 является расчетной областью, шпунт 4,9,10,5,4 -выделен как зона неоднородности. На рис.2 расчетная область н е совпадает с общей областью, так как, приняв эа первоначальное положение кривой депрессии положение 2,3,4, мы отсекли от всей об -
8
лаоти часть 1,2,3,5,1, которая и является расчетной областью.
После привязки расчетной области к оистеме координат происхо -дит запись числовой информации на бланках для последующей набивки на перфокарты.
|
|
< 7 13 19 23 3/ 37 43 49 S5 М 67 73 73 S3 3/ 37& X
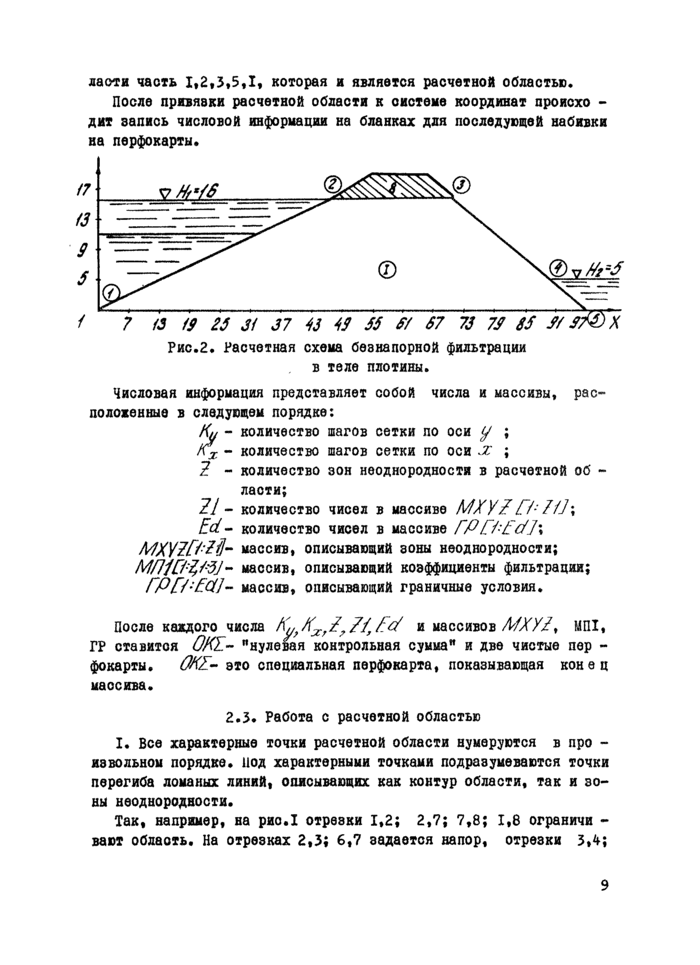
Рис.2. Расчетная схема безнапорной фильтрации в теле плотины.
Числовая информация представляет собой числа и массивы, расположенные в следующем порядке:
Кц - количество шагов сетки по оси у ; пт - количество шагов сетки по оси ;
2 - количество зон неоднородности в расчетной об -лаоти;
21 - количество чисел в массиве MXYZП: Н]\ Ed- количество чисел в массиве ГРП:£сП\ MXV2f/'Z(l- массив, описывающий зоны неоднородности;
массив, описывающий коэффициенты фильтрации;
ГРГ/:ЕС(]- массив, описывающий граничные условия. |
После каждого числа и массивов МХУ2> МП1,
ГР ставится ОКЕ- "нулевая контрольная сумма" и две чистые пер -фокарты. ОКЕ- это специальная перфокарта, показывающая конец маосива.
2.3. Работа с расчетной областью
I. Все характерные точки расчетной области нумеруются в про -извольном порядке, иод характерными точками подразумеваются точки перегиба ломаных линий, описывающих как контур области, так и зоны неоднородности.
Так, например, на рио.1 отрезки 1,2; 2,7; 7,8; 1,8 ограничи -вают облаоть. На отрезках 2,3; 6,7 задается напор, отрезки 3,4;
9
1
4 Распечатка программы в "Методических рекомендациях по расчету плоской (профильной) установившейся филмрацииине приведена из-за ограниченного объема работы. Желающие ознакомиться с программой могут получить ее распечатку на языке АЛГШ1-60 или в кодах машины БЭСМ-4М в институте ВИОГЕЙ.
2
3