етодические указания по применению метода конечных элементов для решения плановых задач фильтрации подземных вод
на ЭЦВМ
Белгород 1979
МИНИСТЕРСТВО ЧЕРНОЙ МЕТАЛЛУРГИИ СССР С0Ю8РУДА
Всесоюзный научно-исследовательский и проектно-конструкторский институт по осушению месторождений полезных ископаемых,специальным горным работам, рудничной геологии и маркшейдерскому делу В И О Г Е М
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ПРИМЕНЕНИЮ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ РЕШЕНИЯ ПЛАНОВЫХ ЗАДАЧ ФИЛЬТРАЦИИ ПОДЗЕМНЫХ ВОД НА ЭЦВМ
Белгород
1979
рис.з, позволяют определить длину /^‘ и /Ц/-ширину ленты тока для каждой стороны треугольника. Легко показать, что
причем, численно
/_ .
|
|
Рис.4. Фильтрационные сопротивления прямоугольного треугольника. |
Для прямоугольных треугольников (рис.4) точка пересечения ме -диатрисс лежит на гипотенузе, и проводимость вдоль нее оказывается равной нулю. Для таких треугольников формулы,определяющие проводимость QU , совпадают с хорошо известными формулами подсчета электрических проводимостей при моделировании на аналоговых электрических машинах.
Для выяснения физического смысла матрицы/т^рассмотрим матричное произведение[т]* [Ь] . где, как и выше, точка над h означает производную по времени. В треугольном элементе проведем ме -дианы (рис.5).
Легко видеть, что
„ [2Ы+Ь +Ы / /А ср] !^ир]
М’т-тг ’
и, следовательно, Vicp означает средний объем жидкости, отнесенный к соответствующему узлу.
Так как
то матрицу [/77] можно назвать матрицей распределения влагоемкости по площади треугольного элемента или просто - матрицей влагоемкости элемента.
Система (5) представляет собой систему трех обыкновенных диф -ференциальных уравнений. Рассмотрим теперь расчетный интервал времени Л Z _
Z+UaZ'Z.
Заменив производную по времени f/jf конечно-разностным отношением 1 J
из уравнения (5) получим следующее рекурентное соотношение:
|
|
hL+h ~2
У///Л - емкостная окрестность узла Ряс.5. Емкостные характеристики треугольного элемента. |
которое позволяет,по известному эначе -нию вектора [hfo в начальный мо м е н т времени, опреде лить значение этого век -тора на расчет н ы й момент времени. Та -кая вычислите л ь н а я процедура носит на -звание схемы Либмана и широко используется при вычислениях.
Исследования показывают, что схема эта устойчива и равно -мерно сходится.
Произведем в уравнении (12) необходимые операции сложения и умножения над матрицами тогда получим следующую основную систему SIK3 для треугольного элемента:
и»
II
|
|
' \© ©X
7®
J dL_ |
7Г
© |
|
|
|
_Ш_ |
| |
N |
,) а,} |
|
©3
4
5 |
• |
□ |
• |
|
|
X |
h, |
|
•
• |
4-
J •
1
+ |
|
|
• |
□ |
• |
|
|
|
|
|
• |
□ |
• |
|
|
к |
• |
• |
|
|
■ |
|
|
|
|
|
|
ZT |
|
|
|
|
|
|
|
IPJ |
|
|
|
flA |
%} |
|
©2з
4
5 |
|
|
|
|
|
X |
S
•к |
|
¥ |
|
|
|
• |
• |
|
• |
|
|
|
• |
• |
|
• |
• |
¥ |
|
|
|
|
|
|
|
|
|
• |
• |
|
• |
hs |
• |
|
|
ш |
|
|
-<
1 |
41 - |
ГУ |
|
/
2
© 3 |
1 |
|
|
|
|
X |
|
— |
— |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
• |
|
• |
5
_1 |
|
4
5 |
|
|
¥ |
• |
• |
Ы |
•
# |
|
|
|
• |
• |
• |
э |
|
|
|
(PJ |
|
|
|
ч |
j |
|
©3
4 |
• |
|
• |
• |
|
X |
hi |
— |
• |
+ |
г |
|
|
|
|
|
|
|
|
Г“
¥ |
|
• |
|
¥ |
¥ |
|
|
¥ |
|
• |
— |
• |
• |
— |
5 |
• |
— |
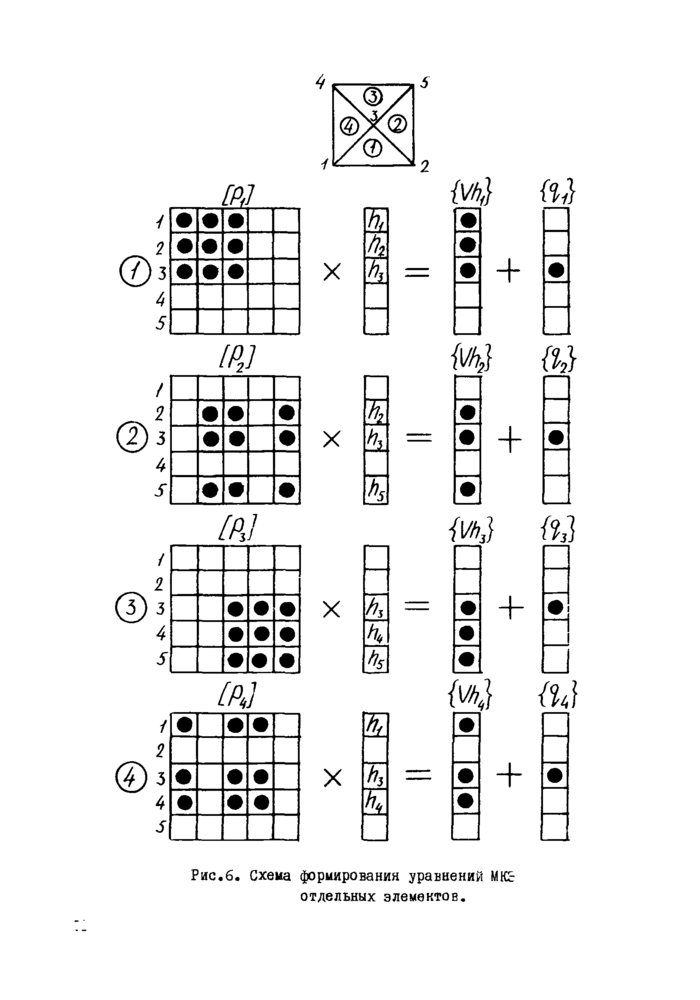
Рис.6. Схема формировании уравнений МКс отдельных элементов.
Чтобы составить систему уравнений для всех неизвестных hi в области фильтрации, нужно теперь объединить уравнения (1з)для всех элементов области. Получается система уравнений вида
где матрица системы [GJ имеет размеры NN *NN у симметрична и обладает ленточной структурой. Составление матрицы [С] для больших NN является трудоемким процессом и производится специальной программой на ЭЦВМ.
Поясним на простом примере, как строится система уравнений (14). На рис.6 показана схема последовательного формирования уравнений (13) для четырех треугольников. Элементы изображены кружками,пус -тые клетки - нулями.
|
|
Рис.7. Схема формирования системы уравнений МКЭ. |
На рис.7 показана структура уравнений системы. В тех клетках, в которых произошло сложение элементов, кружки заменены прямоуголь -никами. Вследствие симметрии матрицы [G] и ее полосовой структуры в оперативной памяти ЭВМ хранится только верхняя полуполоса матрицы шириной /ГА/.
После того, как на расчетный момент буДУт найдены неиз -
вестные напоры hi, hi. hj, h*t, hs , расходы в этих узлах ф/, фг, Qs.Qt fo определятся из уравнения ___
-т,\ ■
Расчет на следующий момент времени Z + 2aZ производится анало -гично, для чего вычисленные значения напоров принимаются за на -
13
чальные условия для этого шага по времени. Процедура вычислений прекращается, если будут исчерпаны все заданные временные шаги. Метод конечных элементов сравнительно просто применяется и для моделирования на ЭЦВМ фильтрации в слоистых толщах, состоящих из водоносных пластов, равделенных слабопроницаемымж глинистыми слоями, Схематически геологическая структура такой трехслойной системы показана на рис,8,
|
///////// / / // / |
|
|
Рис.8. Схема слоистой водоносной системы. |
Задача о неустановившейся фильтрации применительно к такой схеме решается на основе следующей системы уравнений [в]г
3hi д /т,d/ь \ d /т. dAjу. /с d//* /
1ГЯГаГ%,Я<?У 1 *77 Lm J“> j5 ■£ I ■
•* . •«»> где ho - напор в слабопроницаемой прослойке. Применяя ко второму уравнению (15), описывающему вертикальное течение в прослойке, метод конечных элементов, положим
Л,/Z.fcj+fc dr/tj,
!т w
тогда, после преобразования, получим
dho / . At-Ar . Л* / /
1ГГ/г-о " /77 к
- * It t +f *-'■ <“>
Подставив выражения (17) и (18) в систему (15),получим систе -му уравнений
Разбивая верхний и нижний пласты на конгруэнтные треугольники (рис.9), получим следующее основное уравнение МКЭ, аналогичное уравнению (5)
где матрицы-коэффициенты имеют вид ,
rfy7*tfJ ’
~fSj
причем [0,2 и [Q[]~ мат -рицы проводимости для верхнего и нижнего тре -угольника соответствен -но. Остальные обозначе -ния имеют следующий смысл.
Ifcl'/Л *jA)B7;0&fjb£Lj
|
|
Рис.9. Конечно-элементная схема слоисто г. система. |
УДК 681.3:556.3
Настоящие методические указания предназначены для численного моделирования на ЭЦВМ методом конечных элемен -тов (У КЗ) нестационарных плановых задач фильтрации. Программы написаны на языке ФОРТРАН-2. Приводится тестовые пример расчета для случая напорно-безнапорного режима.Авторы программ: Васильев В.А., Карачевцев Н.Ф.,Ломакин А.В., Бабин В.И., Мозговой И.Ф., Муравьева Т.И.
Работа выполнена Васильевым В.А., Карачевцевым Н.Ф., Топчим Г.Е. под обдим руководством канд. физ.-мат. наук, доцента В.А.Васильева и утверждена научно-техничеожим советом института ВИОГЕМ 7 сентября 1978 г. в качестве ме -тодических указаний.
(^/Всесоюзный научно-исследовательский и проектно-конструкторский институт по осушению месторождений полезных ископаемых, специальным горным работам, рудничной геологии и маркшейдерскому делу (ВИОГЕМ), 1978.
I. ВВЕДЕНИЕ
Разработка обводненных месторождений полезных ископаемых связана с проведением ряда мероприятий по осушению водоносных горизон -тов. Этому предшествует решение задач фильтрации подземных вод. Фильтрационные процессы, происходящие в естественных природных условиях, очень сложны и только математические модели позволяют изучать их наиболее полно и достаточно надежно.
В настоящее время бурно развивается вычислительная математика, что неразрывно связано с развитием средств вычислительной техники и в первую очередь быстродействующих ЭЦВМ. Численные методы глубоко проникли во все традиционные методы инженерных расчетов. Более того, как отмечает А.А.Самарский [в] " ... в настоящее время про -явился новый способ теоретического исследования сложных процессов, допускающих математическое описание или математическое моделирование - вычислительный эксперимент, т.е. исследование реальных процессов средствами вычислительной математики".
Вычислительный эксперимент проводится на тщательно подготовленной математической модели процесса, реализованной на ЭЦВМ. Разра -ботанный алгоритм и отлаженная программа образуют действующую ма -тематическую модель. Например, можно создать действующую моде л ь напорного или безнапорного потока в условиях стационарного или нестационарного режима, модель напорно-безнапорного потока, потока, протекающего в слоистой толще, пространственного потока и т.п. Такие модели легко превращаются в постоянно действующие модели кон -кретных гидрогеологических объектов, систем осушения и т.д. Можно с уверенностью утверждать, что, по мере развития вычислительных средств, с появлением ЭВМ новых поколений, вычислительное экспериментирование будет успешно развиваться и расширяться.
Гидрогзологу, не специалисту в области вычислительной математики, трудно ориентироваться в тонкостях современной математики. Практика показывает, что лишь те методы, которые отличаются прос -тотой, наглядностью, способностью удобно согласовывать математи -ческие параметры с геологическими и гидрогеологическими представ -лениями, получили наибольшее распространение в фильтрационных расчетах. К таким методам относятся ЭЦДА* моделирование на аналоговых ЭВМ и интеграторах. С внедрением в практику фильтрационных расчетов ЭЦВМ получил широкое распространение метод конечных раз -ностей (МКР). Однако в силу специфики реализации этого метода на ЭЦВМ гидрогеологу, привыкшему при аналоговом моделировании опери -ровать физически ощутимыми величинами и понятиями,такими,как филь-
трационные сопротивления, емкости, стало труднее следить за про -цессоом моделирования и контролировать результаты, ибо для это-го необходимо более глубоко и профессионально вникать в сферу программирования и математические тонкости той вычислительной схемы, которая заложена в программу, В последние годы стремительно развивается метод конечных элементов (УКЭ), который, с одной сторо -ыы, принадлежит к разновидности УКР, а, с другой» обладает такими же достоинствами, в смысле простоты, нагляднооти, гибкости и физической доступности, что ЭГДА я А ВЫ, Кроме того, этот метод
по целому ряду других достоинств обладает более широкими возможностями, чем метод аналогового моделирования.
У КЗ в настоящее время очень популярен [1,2,3,4,5,7]. В моно -графил "Теория метода конечных элементов" [3] Г.Стренг и Дж.фикс пишут: "УКЭ удивительно успешно применяется в самых различных за -дачах. Он был создан для решения сложных уравнений теории упругости и строительной механики и оказался гораздо эффективнее метода конечных разностей", и далее: " ••• вероятно, конечные элементы стали наиболее употребительным средством вычислительной математики во всем мире". Важной особенностью УКЭ является то, что он очень хорошо реализуется на ЭЦВУ. Как показала практика использования УКЭ в институте ВИОГЕУ [7] , постоянно действующие модели стацио -нарных и нестационарных потоков определенной структуры ( плановые напорные, безнапорные, напорно-безнапорные) позволяют удобно осу -шествлять вычислительный эксперимент. Эти модели легко учитывают фильтрационную неоднородность среды, локальные особенности потока и сложную конфигурацию границ, многовариантность смены граничных условий и параметров. Программы, реализующие метод,надежны и просты в эксплуатации.
Цель настоящих методических указаний - изложить основные вопросы методики численного моделирования на ЭЦВУ по методу УКЭ неста -ционариых плановых задач фильтрации.
2. ПОСТАНОВКА ЗАДАЧ
Уетод конечных элементов применительно к фильтрационным расче -там рассматривается ниже как метод моделирования и осуществления вычислительного эксперимента для плановых нестационарных потоков подземных вод, описываемых обобщенным уравнением Буссинеска [б].
(D
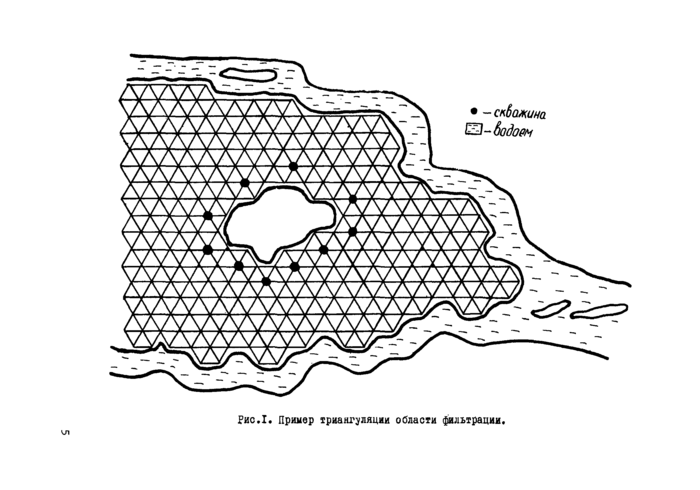
|
• - CK&QAUHQ
ЕЗ-6одо#ч |
|
|
Рис.I. Пример триангуляции области фильтрации. |
где Pr/X.j/J, Aу I PjfcyJ - заданные функции; -на
пор (уровень) грунтовых вод;. 1л/ - интенсивность площадного питания (инфильтрация); t - время.
В зависимости от характера планового потока функции P/.Pz, Рл приобретают следующий смысл:
а) напорный поток А-Таг; /i*7y;AeJt* , где Тх,7у - фильтрационная проводимость пласта в направлении координатных осей;^//# -коэффициент упругой водоотдачи;
б) безнапорный поток fit *Хх//7-/70), Рг* /Су//? ~/7o/i Pj
где Ах, Ку - коэффициенты фильтрации в направлении осей X
- отметка водоупора; JI - коэффициент гравитационной водоотдачи;
в) напорно-безнапорный поток, функции P/,Pi,fis принимают зна -чения,соответствующие пп. а) и б) для соответствующих зон.
В общем случае решение уравнения (I) должно удовлетворять условиям:
2) условие I рода Р/л.j/t c/rf ж У/ /Л.J/J;
3) условие II рода £///,J/,///- г
где ф - расход потока на участке границы /* .
Как и при моделировании на моделях-сетках, идея МКЭ проста: сплошная область фильтрации заменяется дискретной. Дискретиза ц и я производится путем разбивки области на непересекающие друг друга подобласти - конечные элементы. Алгоритм и программы, рассматриваемые ниже, используют конечные элементы в виде треугольников про -извольной формы. Пример такой триангуляции показан на рис Л. Про -нумеруем все треугольники области от I до/У/У, а все вершины их (узлы) - от I до N N •
|
у |
|
|
гия, отнесенная к единице массы, ^
запасенная жидкостью на некого - Q L_
рый фиксированный момент времени,
для треугольника будет опреде - Рис.2. Треугольный конечный |
Выделим какой-нибудь треуголь-
ляться выражением
в
примем последний интеграл берется по периметру треугольного элемента, так что % означает приточность со стороны треугольна -
ков, окружающих рассматриваемый.
Как доказывается в вариационном исчислении, задачу интегриро -вания уравнения (I) можно заменить задачей минимизации функционала (2) fl] , распространенного на всю область фильтрации. Решая эту последнюю задачу, поступим следующим образом.
Предположим, что в пределах треугольника функция h/xytj представима линейной функцией координат,
htxytj. мух, y)hi/tl1 Ц/1. а/1/1. у/ (3)
где (&s 1 ; ^ 1'/ (4)
При этом выражаются через координаты вершин тре -
угольника следующим образом [I,2j:
ас 1Х/ Цх -Xxyl : aj 1X1l/l -Xit/x ; a1 -XtJJi -XJyi;
Ci -T/Г- Xj ; Cj 1XL -XX; LX ~Xl
A [(n -xyKj/i -yxJ-fXi )(yc -у;)].
Теперь интеграл 17 по треугольной области будет функцией узловых значений hi, tyt hx
Чтобы найти минимум 7/1 по переменным % полагаем
Ш-О: £■/>■ £-0-
В результате получим основные уравнения метода конечных эле -ментов для треугольника, которые удобно записать в матричной форме1
Фя11] ft] -{1]■1{$).
где элементы матриц определяются выражениями
П ■!№ Р #' 14 §р р) 14у./Пу-у/Р, /Vi/у аж ay ,Wi -jjw/vi аж ay;
В развернутом виде эти соотношения имеют вид
+ACttyJi у/л*~ {P/&i3* +A£iC*J;fa - ^ tP/ &* + P*C/ c*)>
fa* чfa*fa)/ &/’ ’№*£'*!• £**•-(?* *£>*)'
/пи « myj. , /77ЖЖ = Pj ■£-;
/77tJ * /77i/c ~ Лу< - A y^T * причем, как это легко заметить, матрицы симметричны: Qij - и
ап;*/п;/, w^wf, / = д/.
где фс есть приток в узел L со стороны треугольников, окружа -ющих данный.
Элементы матрицы [Q] имеют простой физический смысл. В развернутом виде уравнения (5) имеют вид
fa/ty -hi) * fir//?* - /и/ + (2/71 * Ад +А/с )ш W-y + (JL;
A Mi * 2Ay + Ax) = h/f-+
$)K/ty -At) +£lk//?l -/?*)+ (hi + Ay +2fa)» Щу +q/c
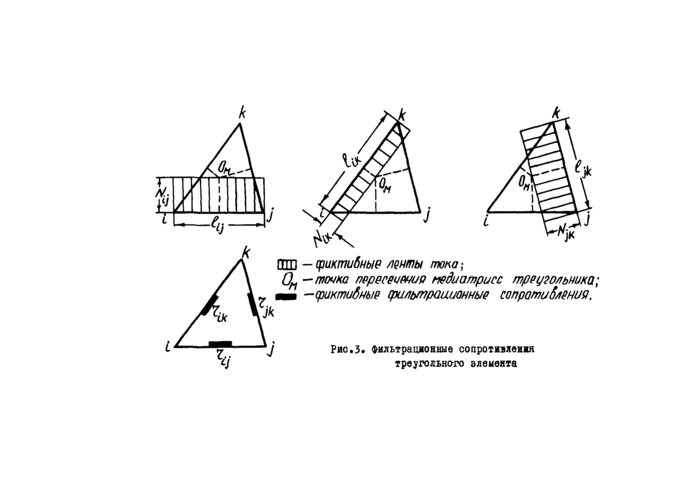
Структура этих уравнений позволяет трактовать коэффициенты д/у как фильтрационную проводимость некоторых фиктивных лент тока, по которым жидкость якобы перемещается от одного узла к другому.Матрицу [д] называют матрицей фильтрационных проводимостей треугольного элемента. Если вместо проводимостей £ij рассматривать величину t так называемые фильтрационные сопротивления,
то можно указать следующую геометрическую схему построения фик -тивных лент тока для треугольника [э]. Вначале определяется точка пересечения медиатрисс треугольника Ом (медиатриссой стороны треугольника называется прямая, перпендикулярная стороне и проходящая через ее середину). Простые построения, показанные на
-сриктибныр ленты топа-,
-точка пересечения меди а трисс треугольника; -сриктибныр (рильтраиионные сопротибления.
Рис.З. фильтрационные сопротивления треугольного элеиента
1
Отчет по теме N® 32-76. Разработка алгоритмов и программ по ре -ализации метода конечных элементов в задачах осушения и геомеханики для ЭЦВМ БЭСМ-ад Фонды ВИОГЕМ, Белгород, 1977, 198 с.
7