ИНСТИТУТ
ГОРНОГОЛЕДА
имени
ДЛСкочииского
А. В. ДОКУКИН, Ю. Д. КРАСНИКОВ, А. А. ШУБИН, И. В. МИХАЙЛИН
МЕТОДИКА РАСЧЕТА ИМПУЛЬСНОГО ПРИВОДА ДИЗЕЛЬНОГО ТИПА
Министерство угольной промышленности СССР Академия наук СССР Ордена Трудового Красного Знамени Институт горного дела им. А. А. Скочинского
Лаборатория динамики горных машин и импульсной техники
Утверждена зам. директора института проф., докт. техн. наук А. С. Кузьмичом 21 октября 1975 г.
Проф., докт. техн. наук А. В. ДОКУКИН, проф., докт. техн. наук Ю. Д. КРАСНИКОВ, докт. техн. наук А. А. ШУБИН, инж. И. В. МИХАЙЛИН
МЕТОДИКА РАСЧЕТА ИМПУЛЬСНОГО ПРИВОДА ДИЗЕЛЬНОГО ТИПА
Москва
1976
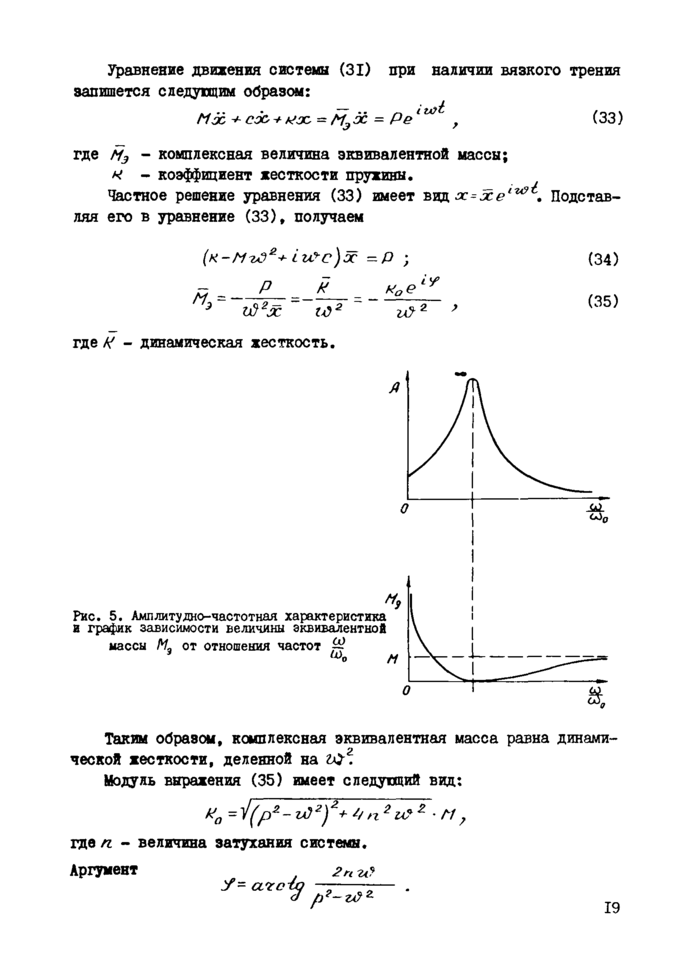
Дифференциальные уравнения движения системы записываются в виде
mx4^Kf(SHi-s)~n-Kz(&ri+$fn ; (II)
*V (^ш ~s) ~ +J*far* J — jc^ * (12)
Но ас, -гг* = SHi - s * поэтому, дифференцируя последнее равенство два раза, получим ос<—эсг = — S , что после подстановки уравнений (I) и (2) дает
s+*&iS-)(s~ > аз)
где М3 - эквивалентная масса, величина которой будет определена ниже.
Уравнение (13) можно написать в следующем виде:
’ (14)
где г*>- скорость движения поршня.
Разделяя переменные и интегрируя уравнение (14), получаем
Так как в рабочей части цилиндра открыты выхлопные и продувочные отверстия, то выражение (15) для скорости поршня, движущегося под действием сжатого воздуха в буфере, принимает вид
^'”с' ■ (16)
Произвольная постоянная Сл определится из условия, что при 5 = 0 а?* О, поэтому
/ V ^
Г = эи Шэ±-т\
Ч -
Подставляя это значение для С4 в выражение (16), получим
Когда величина перемещения поршня s=sfM^ , то выражение (17) будет иметь вид
где $ % § *}*& ~£>нд •
После закрытия выхлопных и продувочных отверстий происходит сжатие воздуха в рабочей части цилиндра. В этом случае выражение (15) имеет вид
Постоянная Сг найдется из условия: если 5 = 0, то &р - ,
тогда
2 w f п
п = /Л - + /Мъ +пг ) о
Lz ^"6 2Ч~%ЯГ)Тп=П'
Подставляя выражение для С2 в равенство (Т8), найдем
7Г?(Ммэт) /7■ (19)
Пользуясь формулой (19), можно для лчбог' значения перемещения поршня s найти величину скорости движения поршня оУр в рабо-
11
чей части цилиндра. Наименьшее значение скорости аГр соответствует моменту воспламенения топлива, что имеет место при
В формулах (17) и (19) перемещения 5 отсчитываются от начала движения поршня в соответствующей части цилиндра.
Среднее значение скорости с достаточной степенью точности (ошибка составляет менее 105?) можно найти^из выражения для средней квадратической скорости: оУср = 0л9шср . Это позволяет,
не прибегая к численному интегрированию, определять время движения поршня за один цикл и число ударов поршня по инструменту.
Средние квадратические значения скорости найдем, интегрируя выражения (17) и (19):
где - общая длина хода поршня.
Рабочий ход поршня (пропесс расширения)
Длина камеры сгорания в момент воспламенения топлива равна
где в - степень сжатия.
Длина буферной части цилиндра с учетом приведенного объема воздушного ресивера для продувки от выхлопных газов составит
' (20) где *%=£«< +8*6 •
Уравнение для определения давления в процессе расширения газов, согласно выражению (10), имеет вид
Дифференциальные уравнения движения системы в случае рабочего хода поршня запишутся так:
(4*)(&s)~s)';
Так как+S , то = g . Подставляя в по-
б
следнее равенство значения для и Jr, иэ формулы (21), получаем
s
Решая уравнение (22), находим
Постоянная интегрирования С находится из условия, что при S^O и)й=0 . Тогда из выражения (23), получаем
Подставляя в выражение (23) равенство (24), получаем
Г'
*4 & г (^£у
|
Значение скорости в момент прохождения поршня черев выхлопные и продувочные отверстия составит |
|
к * * |
|
|
" . /О 71
PSf*[ &* J+PhSShS |
4 [,-$&(£-■')/ |
|
|
\ Xs £ /
L J |
|
.(26) |
Пои прохождении поршня через выхлопные и продувочные отверстия происходит выпуск отработанных газов из рабочей части цилиндра, продувка его с помощью ресивера и снабжение свежим воздухом. После этого поршень нагнетает воздух в оставшуюся буферную часть цилиндра. При этом давление воздуха после закрытия отверстия в ресивер будет равно
pec J нп
Б рассматриваемом случае уравнение (23) принимает вид
2 /т + М9)*п * / \/*~а# „
s ~~нЧ ( тм3 ) Pk5Sk§ ft** ~s) + z •
Постоянная С2 находится из условия, что при з= О ( - скорость движения поршня в момент прохождения его через
выхлопные и продувочные отверстия). Поэтому имеем
Тогда выражение для скорости окончательно примет вид
Интегрируя выражения (25) и (28), находим средние значения квадрата скорости:
Численное интегрирование выражений (25) и (27) показывает, что для рабочего и пускового режимов можно с достаточно;' точностью принимать wcp р = 0,90 го^ .
Пользуясь выражениями для средней скорости, можем найти время движения поршня за один цикл:
г^Ы~ *'■> ’
\ ^ CP /J /
где 3^ - ход поршня;
Мер п / Чло - средняя скорость движения поршня соответ-ственно в пусковом и рабочем режимах;
tj - время задержки воспламенен™ дизельного топ
лива, равное (2f8)J0-3 с.
Число ударов поршня (бойка) по инструменту находится по формуле
п&~~т -
Временем соударения поршня с инструментом,т.е. металла с металлом, пренебрегаем, так как оно по величине на два порядка меньше, чем время движения поршня за один цикл работы двигателя.
Нагружение инструмента происходит через воздушную подушку путем соударения поршня как бойка и инструмента с сохранением неизменным некоторого объема воздушной подушки. Для этой цели в поршне делается полость, содержащая сжатый воздух,где создается давление, достаточное для запуска двигателя.
Таким образом, поршень после закрытия отверстий в ресивере обладает наибольшей скоростью. Дальнейшее движение поршня происходит без приложения внешней нагрузки, при этом накопленная кинетическая энергия движения расходуется на удар поршня по инструменту через воздушную подушку. Энергия, расходуемая на удар, зависит от абсолютного значения скорости.
Для определения абсолютной скорости движения поршня в рабочем режиме преобразуем первое уравнение выражения (21):
djA ds_ _/[_ fs^ffr dt ds ~m U / S S -^-S«S(S«S-S)
или
отсюда находим
dWi
ds
Замечая, что в выражении (29) производная знаменателя равняется числителю, можем воспользоваться следующей подстановкой:
=p(it) [it +s) + (i* ~s)
Тогда выражение (29) можно представить так:
2dZ
Интегрируя это выражение, получаем
(30)
. т
4+ Ны
Для определения перемещений х, и х выражение (30) представим так:
Интеграл этого выражения имеет вид
&
Постоянная £ определяется из условия, что з = 0 при эс = эс0^
( х0/ - начальное положение поршня), следовательно, С-~Х0¥7 тогда
Эквивалентная масса Мз f или критерийf характеризующий реактивное сопротивление колеблющейся .системы
На систему, состоящую из тяговой цепи и двух вращающихся звездочек, растянутых домкратами, передаются колебания от привода (двигателя) импульсной системы. Таким образом, эта система колеблется за счет энергии,периодически передаваемой вынуждающей системой (двигателем).
При этом передаваемая обратно вынуждающей системе энергия настолько мала по сравнению с запасенной в этой системе, что практически ею можно пренебречь» Величина эквивалентной массы является критерием, характеризующим механическое реактивное сопротивление системы, и определяется из выражения
(31)
Вуд ем рассматривать установившееся движение, т.е. когда имеют место только вынужденные колебания» Предположим, что вынуждающая система (двигатель) действует на связанную с ней систему с периодической силой, т.е» простой гармонической силой, приложенной в некоторой точке цепи» Для данного случая можно положить
эс^ = Р sen Cjji .
Подставляя это значение для эсг в уравнение (31) и учитывая, что в рассматриваемом случае можно положить ^ ^ * по
|
|
где г0о иъ02~ угловая частота соответственно собственных и вынужденных колебаний. |
лучаем
(32)
Из равенства (32) видно, что величина эквивалентной массы системы, приводимой в вынужденное колебание, зависит от соотношения частот колебаний (рис. 5). Когда= что соответствует резонансу системы, величина эквивалентной массы М3~ 0. В области частоты глУ% значительно превышающей собственную частоту гОс , существенное влияние на величину массив оказывает величина массы М . Сила упругости цепи почти не влияет на величину мэ . До резонанса, т.е. в области частот , основное влияние
на величину эквивалентной массы оказывает сила упругости цепи.
Таким образом, варьируя параметры системн,ыожно изменять величину эквивалентной массы, т.е. критерий, характеризующий механическое реактивное сопротивление системы.
В целях упрощения пренебрегаем сопротивлением от трения, хотя в действительности оно всегда существует при колебаниях рассматриваемой системы и наиболее значительно при резонансе.
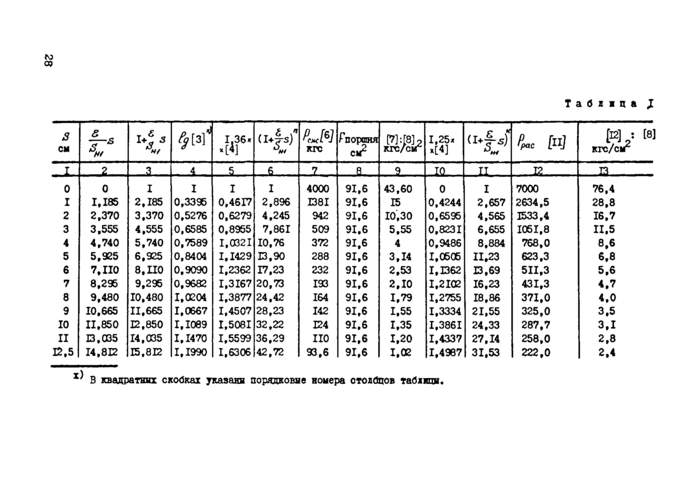
Уравнение движения системы (31) при наличии вязкого трения запишется следующим образом:
Мой + сЗс, + /гос = Мээс = Ре1Ъ°^ , (33)
где Мэ - комплексная величина эквивалентной массы; к - коэффициент жесткости пружины.
Частное решение уравнения (33) имеет вид = Подстав
где И - динамическая жесткость.
Рис. 5. Амплитудно-частотная характеристика и график зависимости величины эквивалентной
массы Ма от отношения частот ~
* /А
ляя его в уравнение (33)* получаем
Таким образом, комплексная эквивалентная масса равна динамической жесткости, деленной на ъ$г.
Модуль выражения (35) имеет следующий вид:
К0 = р2' - 4 п 2 и? 2 * Л/ j
где п - величина затухания системы.
Аргумент
У= иг о то —-“
d
УДК 622.0025-867
В методике изложены вопросы теории импульсного привода со свободно движущимся поршнем как многомассовой системы при адиабатическом и политропном процессах, происходящих в рабочем веществе. На основе термодинамики и теории колебание выведены расчетные формулы для определения основных параметров импульсного привода с учетом влияния на ее работу свойств струговой установки. В качестве примера дан числовой расчет импульсного привода дизельного типа.
Методика предназначена для научно-исс ледовательскиг и проектно-конструкторских организаций, занимающихся проектированием и созданием импульсных струговых установок с дизельным приводом.
((Г) Институт горного дела им. А. А. Скочинского (ИГД им, А. А. Скочинского), 1976
Бели двигатель с подвижным основанием расположить на платформе на роликах, то величина эквивалентной массы будет равна массе подвижного основания двигателя, т.е. Мэ-И9
В заключение заметим, что при расположении основания двигателя на платформе без роликов величина эквивалентной массы может оказаться меньше массы подвижного основания. Это происходит потому, что сила трения скольжения в зависимости от состояния поверхностей соприкосновения вначале с увеличением скорости может уменьшаться, а затем снова увеличиваться, т.е. имеет место падающий участок характеристики силы трения,свидетельствуют о нарастании амплитуд колебаний.
|
|
Рис. 6. Схема импульсного привода с добавочной массой подвижного основания |
Предположим теперь, что подвижное основание двигателя располагается на опоре, перемещающейся, в свою очередь, вдоль забоя упругой тягой (рис. 6).
Дифференциальные уравнения движения для этой системы будут иметь вид
Мэс+ к(эс - ос ) - А/ ос = Р sin ldt\ , %
2 7 \ (36)
л' ~ ) — TC-j Z у
|
Предполагая, что движение есть гармоническое колебание с частотой получаем |
|
где Z - механический импеданс, равный
(37)
ВВЕДШИЕ
Принцип действия статического струга аналогичен принципу резания металла на металлообрабатывающих станках. Однако в отличие от металла горная порода, как правило, обладает значительной неоднородностью и содержит твердые включения, неравномерно распределенные в горном массиве. Кроме того, из-за больших габаритов струговой установки и действующих на нее нагрузок рабочие элементы машины при разработке пород получают значительную деформацию. Поэтому в них за период нагружения, до начала разрушения породы, накапливается достаточно большое количество потенциальной энергии. Вследствие этого при высвобождении потенциальной энергии в момент разрушения породы плавная ритмичная работа статического струга нарушается. В результате возникает значительная перегрузка рабочих элементов машины, приводящая в некоторых случаях даже к их разрушению от случайно попадающихся в породе очень твердых включений.
В отличие от принципа работы статического струга принцип действия импульсного привода основан не на явлении резания, а на ударном разрушении породы.
Динамические процессы, происходящие при работе импульсного привода, можно охарактеризовать как процессы внутренней и внешней динамики системы. Под внутренней динамикой системы понимаются совместные термодинамические и динамические процессы механической системы. Внешняя динамика характеризуется ударным режимом, оказывающим влияние на движение системы, связанной с тяговым устройством.
Импульсный привод представляет собой двигатель-дизель со свободно движущимся поршнем,работающий в двухтактном режиме (рис.1).
3
В настоящее время в Советском Союзе и за рубежом широкое применение получили двигатели со свободно движущимися поршнями* В этих двигателях движение поршня, т*е. его перемещение и око-рость, зависит не только от термодинамического процесса рабочих тел, но и от сил инерции массы поршня, что характеризуется непостоянством величины хода поршня. Поэтому разработка вопросов теории таких двигателей даже в простейших случаях значительно усложняется в отличие от вопросов теории двигателей с кривошипно-шатунными механизмами* В связи с тем,что на термодинамические процессы, происходящие в двигателе со свободно движущимся поршнем, оказывает влияние динамика система (силы инерции масс поршня и подвижного основания, а также сила упругости крепежных приспособлений) , необходимо совместное решение уравнения первого за* кона термодинамики и системы уравнений движения всей динамической системы*
Рис. I. Общий вид импульсного привода
Для двигателей со свободно движущимися поршнями термодинамические и динамические процессы, связанные с движением поршня, описываются совмещенным нелинейным дифференциальным уравнением третьего порядка [ I ] . В этом уравнении значения перемещений поршня выражены в функции времени. Решение такого нелинейного уравнения представляет значительные трудности и возможно только с помощью ЭВМ. .Бели учесть, кроме того, влияние массы корпуса и подвижного основания привода на динамический процесс, а также упругие свойства тягового устройства и закон горения топлива, то получаемое при этом нелинейное дифференциальное уравнение в аде большей степени усложняется. Решение такого уравнения вообще малодоступно для практики.
В настоящей работе термодинамические и динамические процессы системы рассматриваются в совокупности и не в функции времени, а в функции перемещения с учетом влияния массы подвижного основания и упругих свойств тягового устройства. Это позволило
4
проинтегрировать получаемые нелинейные уравнения в замкнутом виде и найти удобные для расчета формулы.
Так как рассматриваемая система импульсного привода имеет две степени свободы, то решение такой системы оказалось возможным только благодаря обобщению силы инерции, содержащей эквивалентную массу. Как показано в работе, определение величины эквивалентной массы, которая в общем виде с учетом затухания является комплексной величиной,не представляет затруднений.
Поскольку процесс горения топлива в основном происходит при достаточно малом перемещении поршня, то при интегрировании уравнения первого закона термодинамики использованы свойства дельтафункции Дирака. В этом случае закон горения топлива не представляет интереса, так как окончательный результат интегрирования от него не зависит.
В работе дан пример числового расчета импульсного привода на основе разработанной методики. Сопоставление расчетных и экспериментальных данных показало их хорошее согласование.
Для оценки целесообразности применения импульсного привода при разрушении пород с различными прочностными свойствами исследовалась работа статического струга в двух основных режимах: нагружения и удара, характеризующегося рядом сколов породы. При рассмотрении работы статического струга учтены силы трения, возникающие между цепью и породой.
ВЫВОД ОСНОВНЫХ УРАВНЕНИИ
Зависимость давления Р от перемещения поршня найдем, пользуясь первым законом термодинамики, который связывает величину давления с величиной перемещения поршня при горении топлива, подаваемого в цилиндр двигателя.
Аналитическое выражение первого закона термодинамики чмеет
вид
dQ = fi(du + db) , (i)
где Q - количество теплоты;
fl - тепловой эквивалент работы;//- 1/427 якал/хгс.м; и - внутренняя энергия; U~U(P, Т...);
L - внешняя работа.
5
Пренебрегая внутренней энергией, затрачиваемой на преодоление сцепления молекул, можно написать
du= |f cLT >
т.е. величина U- функция только температуры Т • Так как внешняя работа L в рассматриваемом случае выражается в изменении объема газа под действием давления Р , то приращение работы будет db-pdd . Подставляя в формулу (I) выражения для dtL и dL , получим
dQ= Apdtf . (2)
Пользуясь известными соотношениями из термодинамики
> dT^-fTd(pV) >
формулу (2) можно переписать:
dQ - d \_рЩ+ fipdl?
или
RdQ = C»cL О] +ДRpdtf.
Заменяя в этом выражении ЛЯ и Я разностью теплоемкостей при постоянном давлении и постоянном объеме ср-с^^ЛЯ , получаем
Р*-с# ..сЩ = c„d (р7?-)+ (Cp-c^pdtf
м = " отношение теплоемкостей;
P = p-F - давление газов.
й(¥*5) ’
- степень сжатия, т.е. отношение рабочего объема цилиндра к объему камеры сгорания;
= закон горения топлива;
S - перемещение поршня;
SH4 - начальная длина рабочей части цилиндра. Решение уравнения (4) принимаем в виде
Л US
Р=р,е ,
где С, и Л - функции от 5 .
Дифференцируя выражение (5), получаем
Подставляя в уравнение (4) выражения (5) и (6), получаем
р(
Пользуясь методом вариации произвольных постоянных для опг -деления неизвестных С1 и , можем написать следующие уравнен
г* ./ . м Л 1 —у—S ■+■ оС т=»- ™ Q
ds '
Решая уравнения (7), получаем:
|
Подставляя эти значения в равенство (5), имеем |
|
|
о |
Произвольная постоянная определяется из условия, что при 5=0 » поэтому
где Ркс^ - наибольшее давление в рабочей части цилиндра при холостом ходе.
IW]
Поскольку горение топлива происходит, как известно, при очень малом перемещении поршня 5 = 5rv , то в этом случае закон изменения скорости горения не представляет интереса, достаточно знать величину выделенного тепла от сгоревшего топлива, т.е.
fir*
где 5ц - расход топлива за цикл;
низшая теплота сгорания топлива;
^ - коэффициент полезного действия;
SCK - перемещение поршня в момент воспламенения топлива. Интегрируя выражение (9), получаем
Р^*7Г + s^f + +
с
Так как в ьт'лем предположении snu« , то окончательно
е
будем иметь
0*&4SY (10)
Пусковой режим mrio-ra двигателя
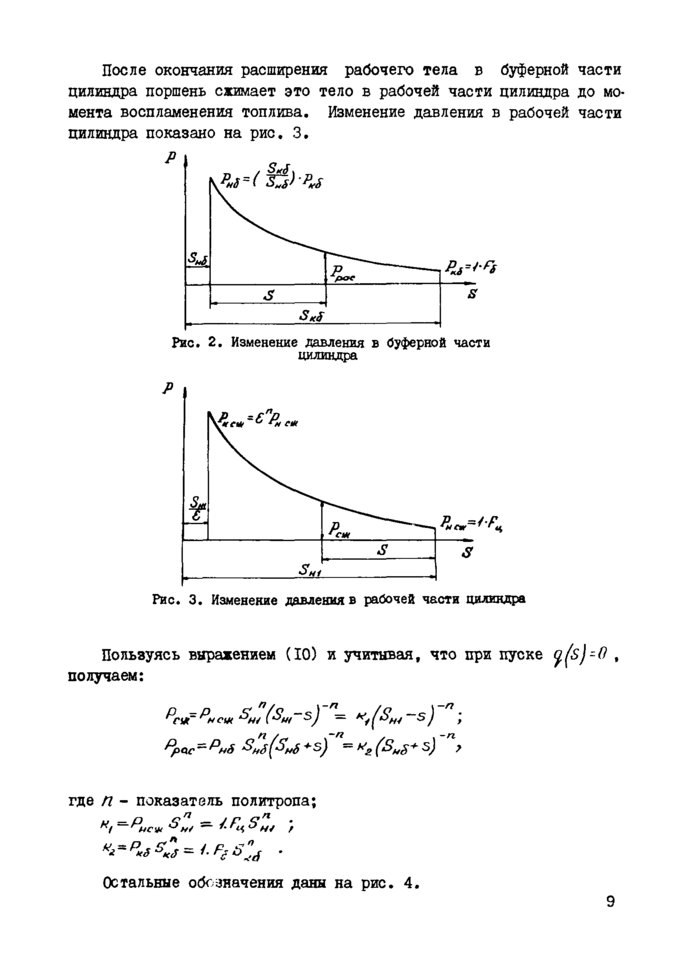
Изменение давлен'* в буферной части цилиндра в зависимости от перемещения порши характеризуется расширением рабочего тела (рис. 2).
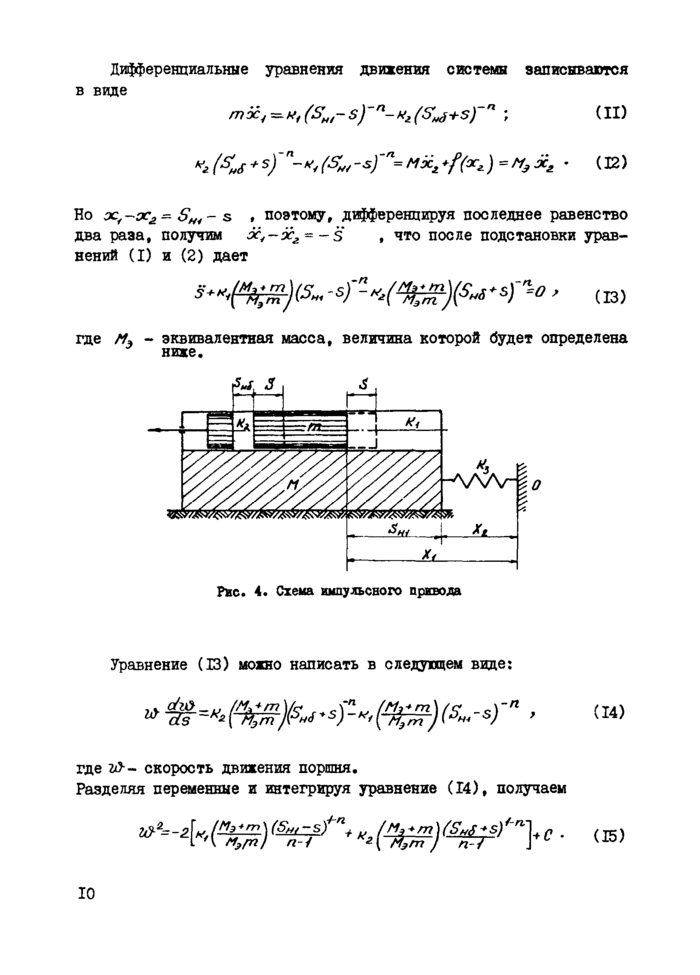
После окончания расширения рабочего тела в буферной части цилиндра поршень сжимает это тело в рабочей части цилиндра до момента воспламенения топлива. Изменение давления в рабочей части цилиндра показано на рис. 3.
|
|
Рис. 2. Изменение давления в буферной части цилиндра |
Пользуясь выражением (10) и учитывая, что при пуске ^(s)~0 , получаем:
где n - показатель политропа; н — P €уП — У Г Яп
Остальные обозначения даны на рис. 4.