Орд«м Октябрьском Рооояюцмм м ордомо Трудового Кроемого Змемоми

ИНСТИТУТ

ГОРНОГО

ДЕЛА

ммами А. А. Скочиисиого

Министерство угольной промышленности СССР Академия наук СССР Ордена Октябрьской Революции и ордена Трудового Красного Знамени Институт горного дела им. А. А. Скочинекого

УТВЕРЖДЕНА

заместителем директора института проф , докт техн. наук А С. КУЗЬМИЧОМ 5 марта 1980 г.

МЕТОДИКА РАСЧЕТА НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ УГОЛЬНОГО ПЛАСТА ПРИ РАЗЛИЧНЫХ СПОСОБАХ УПРАВЛЕНИЯ КРОВЛЕЙ

Москва

1980

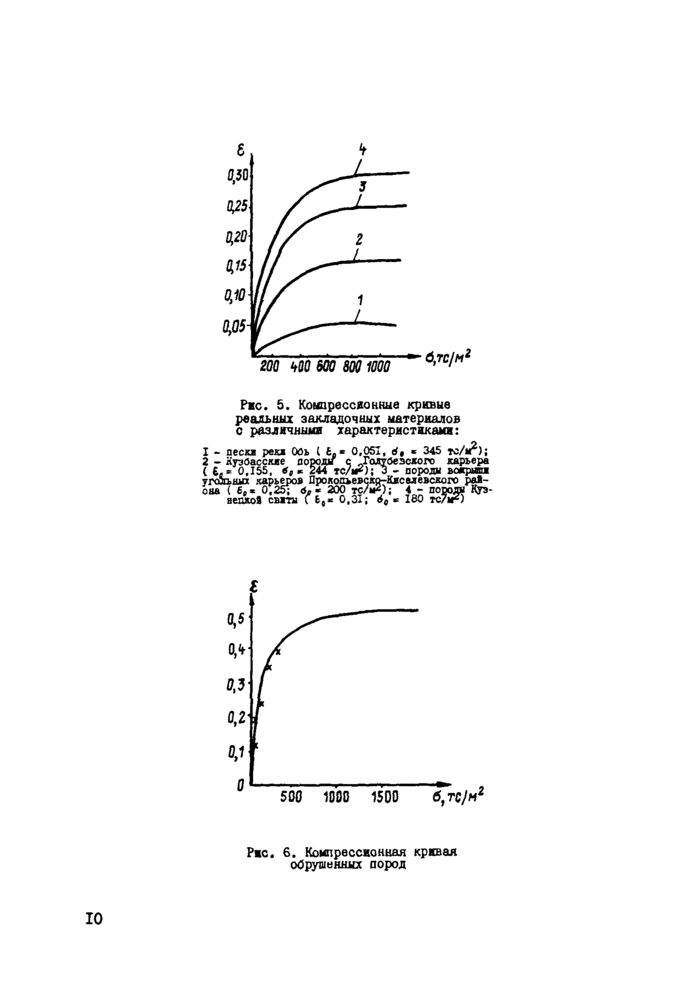
0,051, 6_$ * 345 те/м²); с -Голубе зского карьера ( £- -'0,155,    *    244 тс/мр); 3 - породы ьокрыпш

угольных карьеров Прокопьевско-Киселевского района ( б_в* О,Й; d,« 200 тс/**);    4    -    породы    Куэ-

недлой свита ГЬ,* 0,31;    *    ISO

Типичные компрессионные кривые закладочных материалов [IIJ, построенные по экспериментальным данным, хорошо аппроксимируются экспонентой вида (7). На рис. 5 представлены семейства компрессионных кривых для закладочных материалов, применяемых в Кузнецком бассейне.

В случае полного обрушения зависимость £ от б для слоя обрушенных пород принимается, как и для закладки, но величина £₀ определяется по формуле

(Ю)

где К_р - коэффициент разрыхления обрушенных пород;

К и - максимальный коэффициент уплотнения обрушенных пород ³ под давлением вышележащей толщи;

h - мощность пласта;

h₁ - мощность непосредственной кровли.

Крутизну компрессионной кривой обрушенных пород можно принять по аналогии с крутизной компрессионных кривых бутовых полос, натурные данные о которых представлены на рис.6 крестиками [12]. Построенная здесь по уравнению (5) кривая соответствует £_& = 0,5 и 6_Q » 200 тс/м^.

Применительно к обрушенным породам в расчете приняты некоторые типичные значения:    =    6;    К_р    =    1,2;    Ку = 0,9, подставив

которые в формулу (10) получим £** = 0,5.

МЕТОД И СХЕМА РАСЧЕТА

Рассматривается одиночный угольный пласт под любым углом падения. Разработка пласта осуществляется с закладкой выработанного пространства или с полным обрушением.

Для определения напряженно-деформированного состояния краевой части угольного пласта решается плоская задача теории упругости на основе метода Мусхелишвили [13]. Плоскость сечения выработки проводится вкрест простирания пласта или по простиранию при выполнении условий плоской деформации.

Задача заклинается в том, чтобы найти нормальные напряжения и вертикальные смещения в угольном пласте.

В основу метода решения задачи положен принцип совместности перемещения кровли - почвы, с одной стороны, и закладки или угля, с другой, состоящий в том, что конвергенция кровли - почвы

II

должна быть равна обжатию закладки или угля на соответствующих участках.

Уравнение, выражающее этот принцип, имеет вид

*ГН (^Х) "    (*) ⁼ 86 (*) II'"'⁵ГН ( *) >-    ^(П    5

где    (х) - конвергенция кровли - почвы от действия только

объемного веса пород;

(х) - расхождение кровли - почвы под действием реакции закладки или угля;

8₆ (х) - обжатие закладки шш угля под действием искомого напряжения 6(х);

8_гц(х) - первоначальное обжатие угля под действием веса ^f пород;

(член за двойной чертой учитывается только для угля).

Уравнение (II) справедливо для всей линии пласта - <« с х ^ Однако для упрощения окончательных результатов и возможности применения численных методов на линии пласта выбирается участок - а £ х £ а с таким расчетом, чтобы его концы находились в массиве угля, там, где возмущение, вызванное выработкой, практически затухает. Все дальнейшие соотношения получены именно для такого рабочего участка.

Решение уравнения (II) включает в себя решение нескольких задач; в результате полного решения будут определены нормальные по отношению к пласту напряжения 6 (х) и смещениятИх).

Величину смещений и^(х) определяем, исходя из формул теории упругости [13]:

J7T(^U + LV-) = (i-k'i) *Г(г)-'Р(2)-(г-г)Щг)_}    (12)

где z = x + iy; z = x-Z,t/;

if - смещение по направлению оси у ; и - смещение по направлению оси х ;

£ - модуль деформации массива;

■i - коэффициент Пуассона массива.

Функция ^(z) определяется из соотношения

Ч(г) = /ф (z)dz ,    (13)

где Ф (z) - функция напряжений.

12

Вычисляя интеграл (13), получаем

V(z)=~-(p-lt)('lz^z-a^z -z)(l - — siftrt) •    (15)

Конвергенцию (х) по линии угольного пласта, т.е. при j/=0, и, следовательно, яри z = z, можно определить по формуле (12). В результате подстановки формулы (15) получим в пределах /*/**

k(i-i²)piSH ( х    \    t    т—_г

*_г*(*) =-£-(l — sLnd/JaZ-**, (16)

причем/* в этом уравнении определяется по формуле (3).

Для определения вида второго члена левой части уравнения (II), т.е. ъ₆ (к) , решается .задача о смещениях при условии, что к площадкам кровли и почвы щелевидной выработки приложено искомое нормальное давление 6 (х). Сначала считаем, что оно приложено на бесконечно малой длине d £ с координатой середины площадки х = Расхождение кровли - почвы dt> будет тогда пропорционально величине &($)d f и будет зависеть как от положения 4 площадки, к которой приложено давление, так и от положения х точки, в которой определяется расхождение. Следовательно,оно запишется в виде

о?)

где К(х_} - некоторая функция влияния, подлежащая вычислению.

Если теперь считать, что к кровле и почве на всем участке + д приложено распределенное давление 6(х), то на основе принципа суперпозиции и теоремы о среднем можно записать

-а

13

(18)

Здесь п - количество равных интервалов разбиения участка;

f ' t - координаты соответственно левого и правого концов ⁵к’ ⁵*+i к-го интервала;

6    -    среднее значение искомого давления на к-м интервал

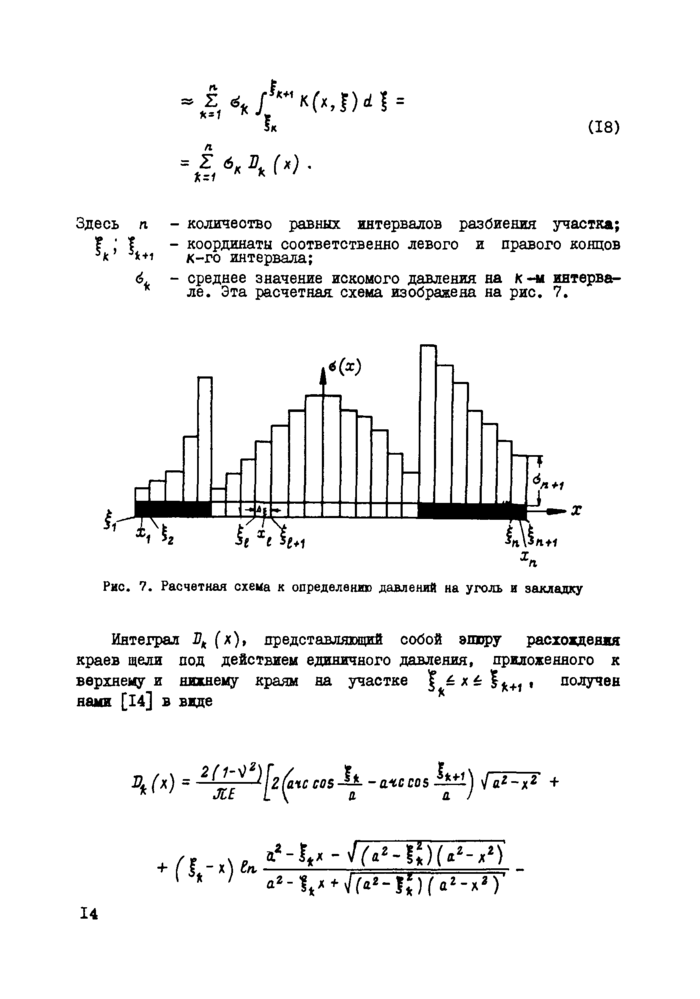
* ле. Эта расчетная схема изображена на рис. 7.

<(*)

Рис. 7. Расчетная схема к определению давлений на уголь и закладку

Интеграл В_к (л)» представляющий собой эпюру расхождения краев щели под действием единичного давления, приложенного к верхнему и нижнему краям на участке ж 6 |*₊₁ , получен нами [14] в виде

14

Для вычисления обжатия закладки и угля, т.е. правых частей уравнения (II), применим обобщенную гипотезу Винклера [14], согласно которой обжатие зависит только от давления, действующего в той же точке. Математически это выражается в виде

$6 (*) = S._L(6)-K- (I =1,2,3) ,    (20)

где S; (б) - деформация, уравнение которой выбирается для закладки и угля из выражений (7)-(9);

h - мощность пласта.

Второй член правой части уравнения (II) (х), выражающий первоначальное обжатие угля от действия веса вышележащих пород, запишется в виде

где В; - деформация угля, уравнение которой выбирается для угля ¹ из ВЕфажених (7)-Т9); I- номер, соответствующий трав-нению, - причем вместо б туда подставляется py/f (I-

-■£^sLnd)•

Таким образом, получив все члены уравнения (II), запишем

= fc.j    fceifplfH(t- 7^s1”*¹)] ■

Требуя выполнения уравнения (22) в дискретном множестве точек

IS

; :> лучим дискретный аналог этого уравнения в виде системы

& \ {*е) ⁶к ^+hsi(i) -

Ь(1-<)²)р1Н Г н    \ J——г

= —г*— {'-т**}**^

+ ft£i ^рТ Н    ^    Sifid

(* = 1,

Уравнение (23) в развернутом виде представляет собой систему из п уравнений с п неизвестными. В левой части этой системы^ входит Как линейно,так и нелинейно - через члены с    Поэто

му решение данной системы уравнений следует производить методом Ньютона-Рафсона [15]. На ( т + 1 )-м шаге итерационного процесса этого метода решается линейная алгебраическая система уравнений относительно неизвестных

,5    ^Г*"    =

= »„ (и)-Mite)J>« (ч) «'Г*/)⁺

+ (l6_t [р ГН () - Sin.)I    (24)

Г I при Ik = I

где

^u [ 0 при к it

Решение этой системы уравнений проведено нами на ЭВМ для различных значений параметров, входящих в эти уравнения.

В результате вычислений получены нормальные напряжения 6у, направленные перпендикулярно линии угольного пласта, и конвергенция пород кровли и почвы D- - 6 fi на участках угольного пласта и закладки.

16

ЗАКОНОМЕРНОСТИ ИЗМЕНЕНИЯ НАПРЯШНО-ДЕЗЮРМИРОБАННОГО СОСТОЯНИЯ КРАЕВОЙ ЧАСТИ РАЗРАБАТЫВАЕМОГО УГОЛЬНОГО ПЛАСТА В ЗАВИСИМОСТИ ОТ РАЗЛИЧНЫХ- ГОРНО-ГЕОЛОГИЧЕСКИХ И ГОРНОТЕХНИЧЕСКИХ ПАРАМЕТРОВ

Основными параметрами, влияющими на напряженно-деформированное состояние разрабатываемого угольного пласта, являются коэффициент бокового распора, глубина разработки, компрессионные характеристики закладочного массива и его отставание от забоя, свойства угольного пласта и наличие в нем неоднородностей.

Влияние напряженного состояния нетронутого массива

Коэффициент бокового распора fi, характеризующий напряженное состояние нетронутого массива, как следует из формул (2),    (3)    и

(22), является параметром, от которого зависит напряженно-деформированное состояние угольного пласта при его разработке.

Для примера рассмотрим крутой угольный пласт мощностью 3 м с углом падения 70°, разрабатываемый на глубине 400 м с закладкой выработанного пространства, компрессионные характеристики которой приняты близкими к аналогичным характеристикам гидрозакладки, а именно: 6₀ = 0,15 и 6_Q= 200 тс/м². Модулй деформации вмещающих пород и угля взяты соответственно 200000 и 20000 тс/м². Для приведенных условий рассматриваются три случая, отличающихся коэффициентами бокового распора:

j9= 0,5; 1,0 и 2,0.

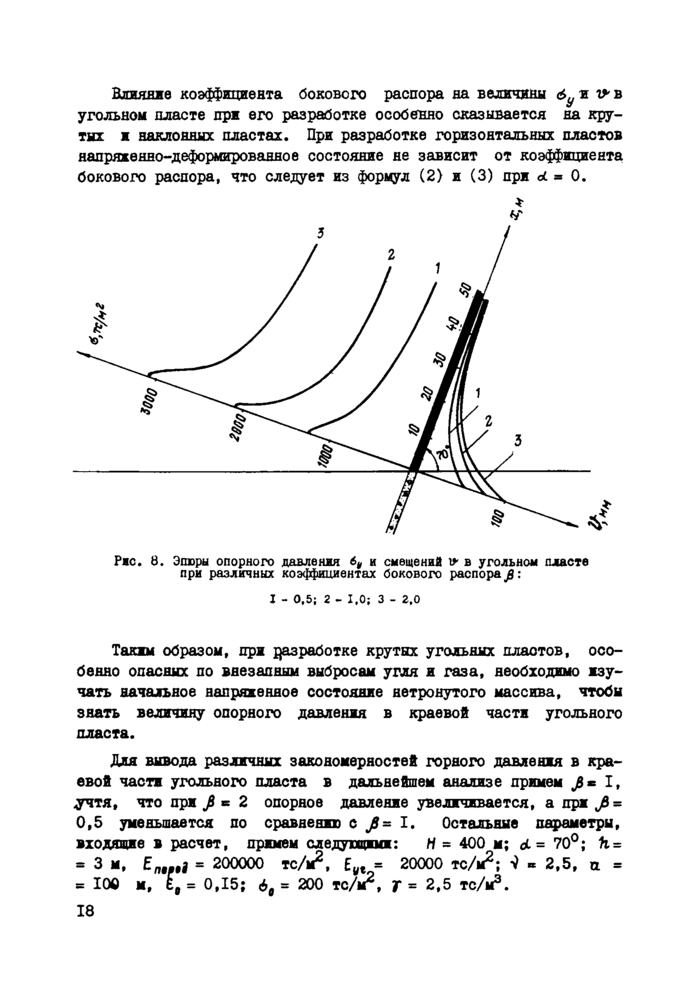
На рис. 8 приведены эпюры опорного давления на угольный пласт и кривые, характеризующие полуобжатие угольного пласта. Из представленных графических данных следует, что опорное давление в краевой части угольного пласта наибольшее при /= 2,0; оно достигает в этом случае 3100 тс/м², в то время как при ^=0,5 1250 тс/м², т.е. в 2,5 раза меньше. Обжатие крутого угольного пласта также интенсивнее при больших значениях коэффициента бокового распора. Так, при fi = 0,5 полуобжатие т* = 55 мм, а при fi к 2,0 оно увеличивается до 100 мм.

Большое опорное давление при ^=2,0 формируется под действием начального напряженного состояния нетронутого массива,!! оно проявляется при разработке пласта.

17

Вяняняе коэффициента бокового распора на величины 6у и V'B угольном пласте при его разработке особенно сказывается на крутых и наклонных пластах. При разработке горизонтальных пластов напряженно-деформированное состояние не зависит от коэффициента бокового распора, что следует из формул (2) и (3) при * 0.

Таким образом, при разработке крутых угольных пластов, особенно опасных по внезапным выбросам угля и газа, необходимо изучать начальное напряженное состояние нетронутого массива, чтобы знать величину опорного давления в краевой части угольного пласта.

Для вывода различных закономерностей горного давления в краевой части угольного пласта в дальнейшем анализе примем jS* I, учтя, что при fi в 2 опорное давление увеличивается, а при fi -0,5 уменьшается по сравнению с fi~ I. Остальные параметры, входящие в расчет, примем следующими:    Н    =    400    ы;    <£=    70°;    h    =

= 3 м, Е_м-_#| = 200000 тс/м², Е_уг = 20000 тс/м²; * 2,5, а = = ме м, Е, = 0,15; 6_в = 200 тс/м², Г = 2,5 тс/м³.

18

Влияние глубины разработки на надряженно-дефошированное состояние краевой части крутого угольного пласта яри разработке с закладкой выработанного пространства

Для выявления закономерностей горного давления на разных глубинах разработки рассмотрен крутой угольный пласт, разрабатываемый с закладкой выработанного пространства на глубине 400, 800 и 1200 м.

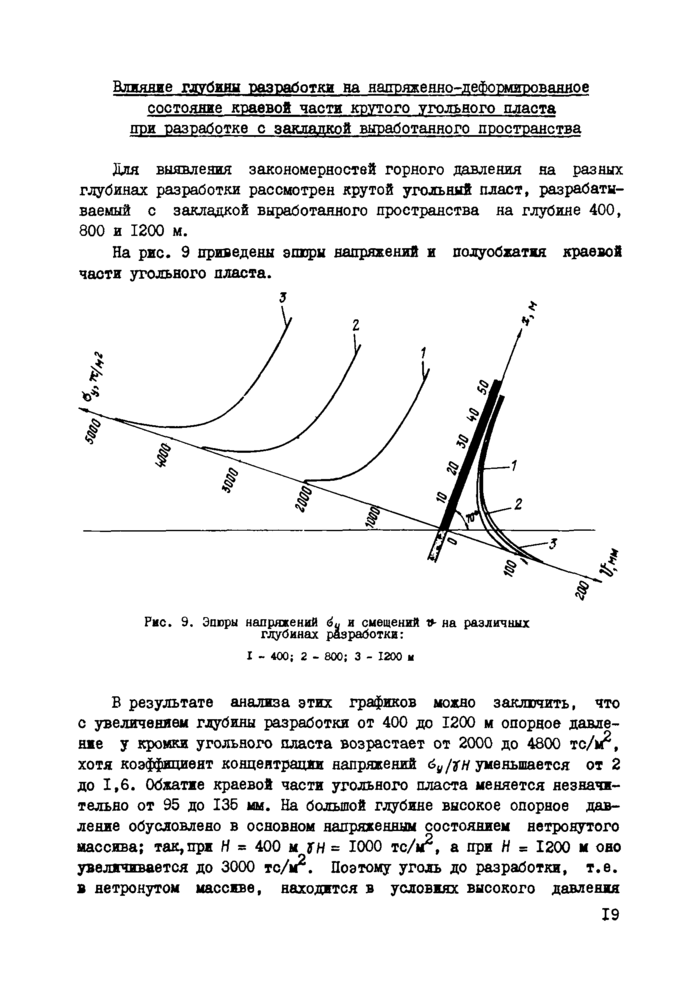
На рис* 9 приведены эшоры напряжений и полуобхатия краевой части угольного пласта.

В результате анализа этих графиков можно заключить, что с увеличением глубины разработки от 400 до 1200 м опорное давление у кромки угольного пласта возрастает от 2000 до 4800 тс/м², хотя коэффициент концентрации напряжений 6_У /jfH уменьшается от 2 до 1,6. Обжатие краевой части угольного пласта меняется незначительно от 95 до 135 мм. На большой глубине высокое опорное давление обусловлено в основном напряженным состоянием нетронутого массива; так,при Н = 400 м ZH = 1000 тс/м², а при Н = 1200 м оно увеличивается до 3000 тс/м². Поэтому уголь до разработки, т.е. в нетронутом массиве, находится в условиях высокого давления

19

УЖ 622.d3I.24

Приведены методика определения напряжения и деформации в угольном пласте, залегавшем под любым углом, при разработке его о закладкой выработанного пространства или с полным обрушением, а также закономерности изменения напряженно-деформированного состояния в пласте в зависимости от коэффициента бокового распора, компрессионных характеристик закладочных материалов и обрушенных пород, глубины разработки и наличия неоднородностей в угольном пласте.

Методика предназначена для работников научно-исследовательских и проектных организаций,занимающихся проектированием систем разработки.

Институт горного дела им. А. А. Скочинского (ИГД им. А. А. Скочинского), 1980

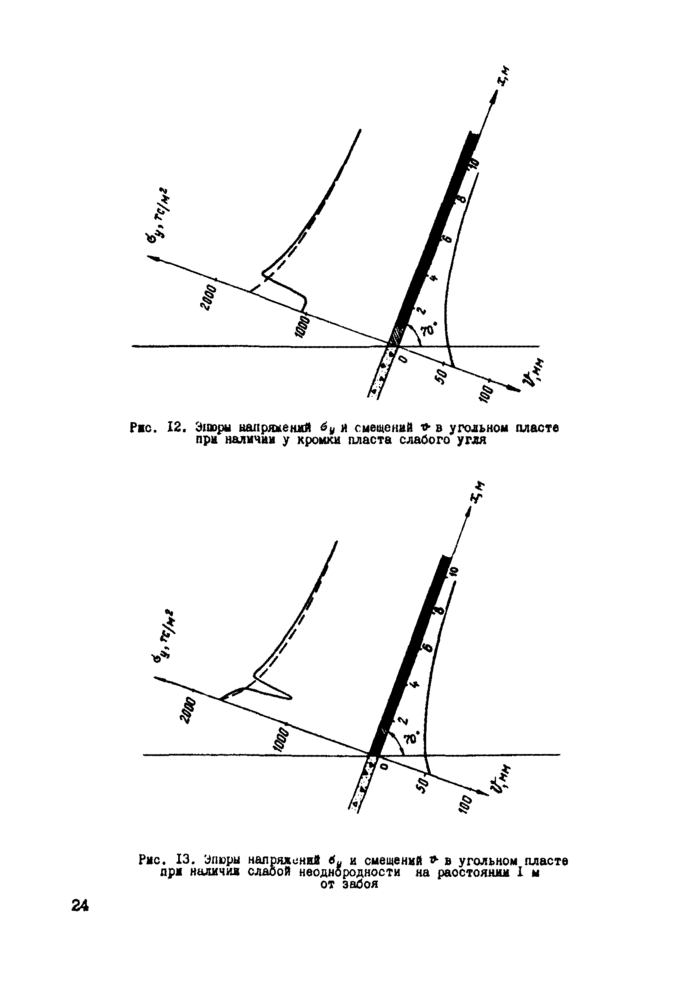
и сального обжатия. Такие проявления горного давления характерны при управлении кровлей закладкой с усадкой в 15%, а при управлении кровлей полным обрушением напряжение 6у и обжатие угольного ддаста значительно возрастают.

Влияние способа управления кровлей на напряженно-деформированное состояние

краевой части крутого угольного пласта

При разработке угольных пластов с закладкой выработанного пространства необходимо выявить влияние свойсте закладочных материалов, а при способе управления полным обрушением - свойств обрушенных пород на напряжения 6 и смещения ^ в краевой части угольного пласта.

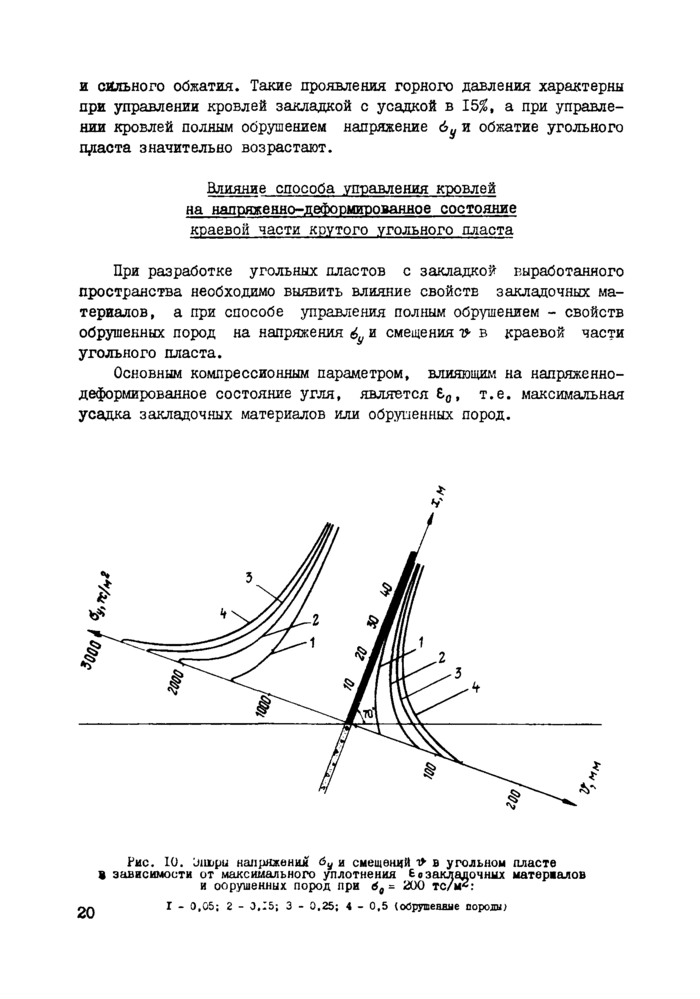
Основным компрессионным параметром, влияющим на напряженно-деформированное состояние угля, является £₀, т.е. максимальная усадка закладочных материалов или обрушенных пород.

ВВЕДЕНИЕ

С переходом горных работ на более глубокие горизонты резко возрастает горное давление и .увеличивается возможность возникновения внезапных выбросов угля и газа, поэтому важное значение приобретает задача изучения напряженно-деформированного состояния краевой части угольного массива, особенно при выемке выбро-соопасных пластов*

Основными параметрами, от которых зависит напряженно-деформированное состояние разрабатываемого угольного пласта, являются глубина разработки, коэффициент бокового распора нетронутого массива, способ управления кровлей, компрессионные характеристики закладочных материалов и структурные свойства угольного пласта, Учесть наиболее полно вбе эти параметры и вывести закономерности Изменения горного давления возможно лишь при применении аналитических методов расчета, поэтому возникла необходимость создания методики расчета напряженно-деформированного состояния угольного пласта с учетом всех перечисленных параметров.

СВОЙСТВА И СОСТОЯНИЕ МАССИВА ГОРНЫХ ПОРОД,

УГОЛЬНОГО ПЛАСТА И ЗАКЛАДОЧНЫХ МАТЕРИАЛОВ

Угольный пласт и вмещающие его горные породы находятся в напряженно-деформированном состоянии, вызванном весом вышележащих пород.

При определении напряженного состояния угольного пласта необходимо ввести две системы координат ;рис. I): одну, ориентированную по гравитационным силам, и другую, ориентированную по залеганию пласта.

3

Напряженное состояние нетронутого массива относительно первой из них х'у¹ определяется компонентами напряжений

;

6⁰xl=jnr(H-y'))    (I)

^тх'у^,=0 >

где Н - глубина залегания пласта в центре очистной выработки;

J3 - коэффициент бокового распора.

Компоненты напряжений 6°_я, 6% и t°_y относительной наклонной системы координат ху определяются из выражений

В результате проведенных экспериментов установлено, что для: условий Араличевского района (шахта км.Орджоникидзе; горизонтальная составляющая нормальных напряжений нетронутого массива больше вертикальной в 2-3 раза, т.е. J3 = 2-^3. Для условий Про-копьевско-Киселевского района (шахты "Ноградская" и "Коксовая’*) получено, что вертикальная составлявшая больше горизонтальной в среднем в 2 раза, т.е. J3 = 0,5. Следовательно, различные районы Кузбасса характеризуются разной величиной коэффициента бокового распора. Поэтому для таких районов необходимо знать конкретные значения коэффициентов бокового распора.

В некотором приближении можно принять, что слоистый горный массив со сцеплением по контактам слоев до начала расслоения является нвазполнородным, причем слои предполагаются тонкими и с одинаковыми иди близкими модулями упругости.

Горный массив принимается также кваз низ о троп дым, т.е. отношение модулей упругости, измеренных вдоль и поперек напластования, близко к единице. Существует большое количество экспершен-тов, подтверждающих это положение [в, 7].

Так как большинство горных пород обладает свойствами ползучести, трещиноватости, то массив принимается не упругим, а ли-нейно-деформируемым. Это означает, что связь между напряжениями и деформациями принимается линейной, но вместо кубякового модуля упругости берется величина модуля деформации всего массива с учетом трещиноватости, слоистости и ползучести пород. При длительной ползучести деформация пород возрастает, а следовательно, модуль деформации уменьшается.

Из экспериментальных кривых ползучести можно получить зависимость модуля деформации массива от времени в виде

еМ = е„ + (е_-е„)(»-Д),    ¹⁵¹

где Е₀ - модуль деформации в массиве в начальный момент воемени при t = 0;

Ео*- модуль деформации массива при t =    ,    т.е.    в установив

шемся состоянии;

£₀ - параметр скорости изменения модуля деформации.

Анализируя данные работы д.С.йржанова [8], можно заключить, что отношение E_Q : Е^ дая песчаника приблизительно равно 1,5-2,0, для алевролита - 3,0 для аргиллита - 3,7, т.е. колеблется в диапазоне 1,5-3,7.

6

Трещиноватость и различные ослабления тоже снижают модуль деформации массива, не меняя линейного характера его деформирования. Это положение достаточно хорошо подтверждено экспериментальными замерами мгновенного модуля деформации в массиве с помощью прессиометра [9]. Эти замеры показали, что коэффициент уменьшения модуля равен 2,5-3,5. Для интерпретации этих явлений К.З.Рупденейтом и И.В.Тарасовой предложена механическая модель трещиноватого массива [10]. Согласно этой модели, трещиноватость и различные ослабления в массиве снижают пропорционально их размерам модуль деформации массива, а общий характер деформирования массива в модели остается линейным.

Так как уравнения теории упругости для определения напряжен -но-деформированного состояния тела основаны только на предположении о линейной связи между напряжениями и деформациями независимо от величины параметров, то к массиву можно применить методы теории упругости, а модуль упругости массива Е_уПр в расчетах можно заменить модулем деформации массива Е, уменьшенным за счет ползучести, трещиноватости и слоистости пород:

£ = Еу_Пр/ К.    16)

Общий коэффициент уменьшения модуля упругости К, согласно вышеприведенным данным, можно взять как произведение крайних значений коэффициентов 4-13 в зависимости от свойств пород. Для приближенных расчетов общий коэффициент обычно принимается равным 10.

При разработке угольных пластов с закладкой выработанного пространства необходимо изучить свойства и состояние углей и закладочных материалов. Обычно закладочные материалы обладают нелинейной характеристикой уплотнения [II], а для: углей характерны как линейные, так я нелинейные деформации.

Поэтому при учете свойств угольного пласта и закладки в решении задачи о напряженно-деформированном состоянии краевой части угольного пласта вводятся аналитические зависимости, характеризующие деформационные свойства этих материалов. Нами предложены несколько типов аналитических зависимостей В =/(б) между напряжением 6 и деформацией 6 при одноосном сжатии:

I тип

Б=&₀(7-_е"^й«) = 6₇(<5);    (7)

7

Ш тип

S =b°tri б0-б ~ ъг(6) >
Е = 80

(8;

(9)

где £ - относительная деформация;

6 - напряжение;

Ь_ол6₀,т - характеристики материала.

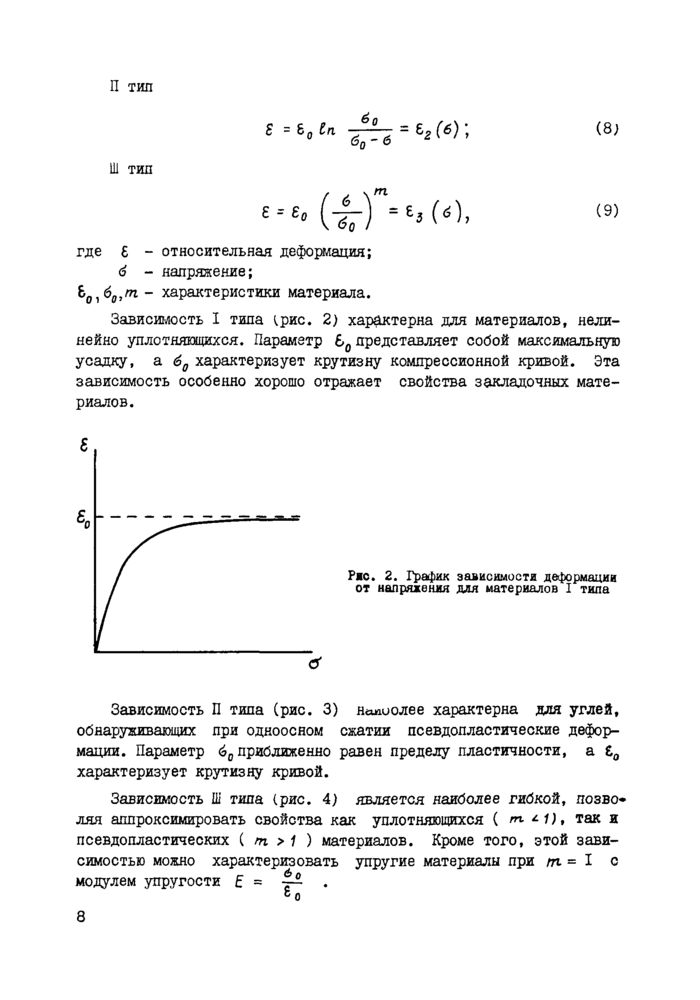
Зависимость I типа (рис. 2) характерна для материалов, нелинейно уплотняющихся. Параметр Ь₀ представляет собой максимальную усадку, а 6₀ характеризует крутизну компрессионной кривой. Эта зависимость особенно хорошо отражает свойства закладочных материалов.

6

Рис. 2. График зависимости деформации от напряжения для материалов I типа

б

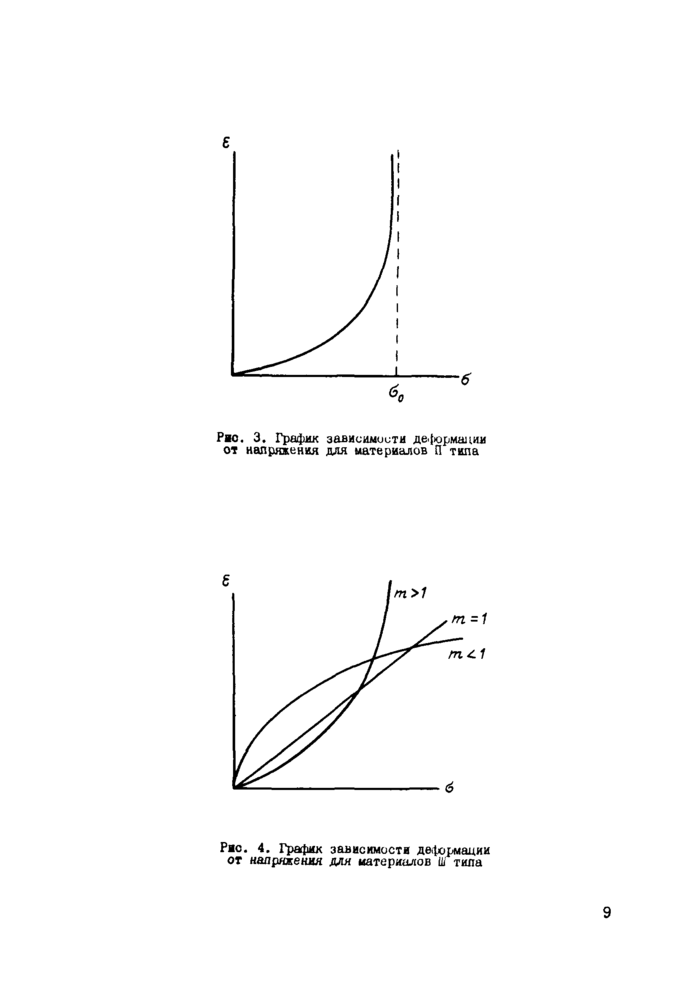
Зависимость П типа (рис. 3) Нешиолее характерна дая углей, обнаруживающих при одноосном сжатии псевдодластические деформации. Параметр 6₀ приближенно равен пределу пластичности, а t₀ характеризует крутизну кривой.

Зависимость Ш типа (рис. 4) является наиболее гибкой, лозво* ляя аппроксимировать свойства как уплотняющихся ( т * 1), так и лсевдопластических ( т > 1 ) материалов. Кроме того, этой зависимостью можно характеризовать упругие материалы при tn = I с модулем упругости Е =    —    .

8

Pic. 3. График зависимости де.|юрмации от напряжения для материалов П типа

Рмо. 4. График зависимости деформации от напряжения для материалов Ш типа

9