|
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ |
|
i@t
Il€ У ДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ (Госстандарт СССР)
Всесоюзный научно-исследовательский институт по нормализации в машиностроении (ВНИИШШ1)
Утверждены
Приказом ВНИИНМАШ » 2?4 от 03.5Л96Г7Г,
Расчеты и испытания на прочность
Метца ко печных элементов и программы расчета на ЭШ пространственных элементов конструкций в упругопластической области деформирования
Рекомендации Р 50-54-42-88
2,1,9. Компоненты тензора напряжений в упругой области деформирования определяются через компоненты тензора деформаций яри помощи обобщенного закона Гука [241 :
&iJ- C'-JKt6Ke. (2.14)
Для изотропного тела компоненты тензора упругих постоянных CtJK^ выражаются через коэффициенты Ламе Я ж i; , в общем случае зависящие от температуры,
'■ ?и »
С~Е(Т) ,$‘д(Т) - значение модуля Юнга и коэффициента Пуаооона при заданной температуре.
2.2. Основные гипотезы термопластичности. Уравнения состояния
2.2.1, Зависимость между напряжениями и деформациями эа пределом упругости устанавливается на основе уравнений теории течения. Предполагается, что упругие свойства и диаграмме деформирования материала зависят от температуры.
2.2.2. Теория пластического течения о изотропным упрочнением при яензотермичеохях процеооях нагружения базируетоя на следующих основных принципах [II,16] .
I. Материал тела однородный и изотропный, изменение его обьеме линейно-упругое;
II
P
£к« - Ot
2. Компоненты тензора приращений полных деформаций cf£\j
состоят из приращений упругих , пластических йсч
т
и температурных d£tj / составляющих
cLt,] = d£tj + d£?j d£cj. (2.i7)
Приращения температурных деформаций определяются выражениями
[24J
d£[j = drdTfycj f (2.18)
где dT-dr(T) - значения коэффициентов линейного теплового расширения при заданной температуре, cJT - приращение температуры в данной точке.
3. Область упругих деформаций при активном нагружении для любого напряженного состояния в пространстве напряжений ограничивается поверхностью нагружения
f(FL', а?, т)*о9 (2.19)
где 3? - параметр пластичности Одквиста. Функция текучести / характеризует переход материала из упругого ооотоявия в пластическое. В частности, при £ < 0 - материал деформируется по упругому закону, при / =0 наступает состояние текучеотн.
Принято, что состояния / > 0 не может быть реализовано.
4. В случае ассоциированного закона пластнчеокого течения компоненты тензора приращений плаотичеокой деформации пропорциональны производным функции текучести по компонентам тенвора напряжений:
p
d£^j - dj Qj$)
где dJ. - некоторый неопределенный не отряда тельный скалярный
множитель. Соотношения (2.20) означают, что пластическое течение развивается по нормали к поверхности текучести.
2.2.3. Принимая гипотезу изотропного упрочнения [II], уравнение поверхности нагружения при условии текучести Мизеоа запишем в виде
(2.21)
где Zs - предел текучести при чиотом одвиге, SLJ - компоненты девиатора напряжений:
(2.22)
(2.23)
2.2.4. Принимается ассоциированный закон пластического течения. Тогда на основании (2.20) компоненты тензора приращений пластических деформаций однозначно связаны о компонентами девиатора напряжений соотношениями
(2.24)
13
2.?.5. В случае яеизотермического процесса деформировался принимаются предпосылки о функциональных зависимостях
- f?s (Я?> Т) I
(2.25)
ЗБ - JVj бЬр> d£° .
Для определения закона ооотояния необходимо для каждого конкретного материала задать скалярную функцию Ts , зависящую от па-раметра & , фиксирующего иоторию нагружения, и температуры ГГ,
2.2.6. Установим зависимость между приращениями напряжений и пластических деформаций.
Поскольку при пластическом деформировании изображающая точка остается на поверхности нагружения, выполняется равенство
di - <**' ' %- ЧГ ' Ц в» -О. <2.26,
Для принятой поверхности нагружения (2.21)
df = S,j dSiJ - dT + 0 dzbo. (2.27)
С учетом иввеотного соотношения
Slj dSLj-- SLJ d^d (2.28)
|
перепишем (2.27) в виде |
|
(2.29) |
Из (2.25) о учетом (2.24) и (2.21) получим
V. wo -
аде = у ал ь s.
Подставив (2.30) в (2.29), найдем неопределенный множитель йл
аз. , (г-31)
(Г
где обозначено:
/ г L/lfS* д t-s
г ~ чь LS + т ^ ^ ,
Тогда связь между приращениями напряжений и деформаций представляется в виде
d^j = с *l(d£*e - d£h) -(рч- QL/) dr, (2.зз)
где введены следующие обозначения:
15
3. МЕТОД РЕШЕНИЯ
3.1. Метод конечных элементов для решения пространственных задач термоплаотичности
Метод конечных элементов (МКЭ) [ 10J эффективен при решении широкого круга краевых эадач меха-ханики оплошной среды. Одним из направлений развития МКЭ является распространение на физически нелинейные задачи. В данной работе рассматривается подход^ основании^ на методе переме-щений^н его применение к исследованию упругопластического деформирования пространственных конструкций. Вывод уравнений для конечных элементов и их объединение в систему уравнений осуществляется на основе вариационных методов. Предлагаемая схема вывода соотношений МКЭ [21,22] позволяет учеоть основные свойства жестких смещений для язопараметрических конечных элементов, компоненты деформации которых зависят от производных жестких вращений и от поступательных и вращательных смещений каждого элемента в целом, и извеотна как монентная схема конечных элементов (МСКЭ).
Процесс решения задач механики твердого тела по МКЭ состоит из следующих этапов:
1) дискретизация области на конечные элементы;
2) введение интерполяционных функций, т.е. аппроксимация ноля перемещений внутри конечного элемента через значения перемещений в узлах элемента;
3) вывод уравнений для каждого элемента;
4) объединение уравнений элементов в единую систему для всей рассматриваемой области;
5) решение общей системы уравнений;
16
6) вычисление искомых полей перемещений и напряжений.
5 предлагаемых рекомендациях рассматриваются в основном второй, третий и пятый этапы. При этом учитывают, что имеют* ся фундаментальные разработки метода конечных элементов^ 10,24]
Принципы и ооновные положения МСКЭ изложены в Приложении.
3.2. Библиотека конечных элементов ППП "Куб"
3.2.1. Для обеспечения проотрвнотвенных расчетов в ПИП "Куб" применяются различные типы КЭ в зависимости от геометрической сложности конструкции, ресурсов машинного времени, оперативной и дисковой памяти.
3.2.2. Для пространственных конструкций, объем которых
можно аппроксимировать конечными элементами прямолинейной формы, вводится предположение, что КЭ ввиду малости его размеров можно принимать в форме косоугольного параллелепипеда и подучат коэффициенты MS в аналитической форме. Для конструкции олокной формы с криволинейной границей возможно применение криволинейных КЭ в виде произвольных шестигранников о численным иитегри реваншем по объему элемента и аппроксимацией координат и перемещений с помощью полиномов Лпграпже от Г до 3-й степени по трем напревлгнипм и включает КЭ о полилинейной, поли-
квадратичной, нолику бичеокой ттрокоимипией и их комбинациями по раз.личным направлениям.
3. •!. 'К ''нойстта элемечт"в. Нччиодонт Mi элементов осум**
'•ГЧОО'М'Ч? п <nv>7f»ГНИЯ г r<\vi т >ПИ;?МИ W'’Q. Д.ЛН Я/РМСН ГОР •
17
численным интегрированием до объему вычисление коэффициентов выполняется по стандартным программам. Ш конечных элементов с аналитическим интегрированием вычисляются по отдельным программам. КЭ с аналитическим интегрирование по объему для вычисления коэффициентов Ш требует в шесть раз меньше времени, чем полилинейный элемент с численным интегрированием. Поэтому для тыл, близких к призматическим и с прямолинейными границами, можно рекомендовать применение КЭ о аналитическим интегрированием при незначительном сгущении сеточной области. Значительное сгущение сеточной области приводит к увеличению ширины строки ЫЖ, что ведет к увеличению времени вычисления U3K всей конструкции. Поэтому для трехмерных тел сложной формы с криволинейными границами следует применять криволинейные элементы о численным интегрированием.
3.2.4. Данные для элементов. Вое величины, относящиеся к элементам, могут быть переменными. Свойства материалов, нагрузки могут задаваться для групп элементов и зависят от номера узла, принадлежащего данному элементу.
3.3. КЭ в форме косоугольного параллелепипеда
З.ЗЛ. Конечные элементы в форме параллелепипеда (косоугольного и прямоугольного) имеют ту особенность, что метрические характеристики местной системы координат постоянны в объеме элемента и коэффициенты матрицы жесткости можно получить в замкнутой форме.
Предполагается, что компоненты тензора преобразования координат в объеме алемеита постоянны;
(3.1)
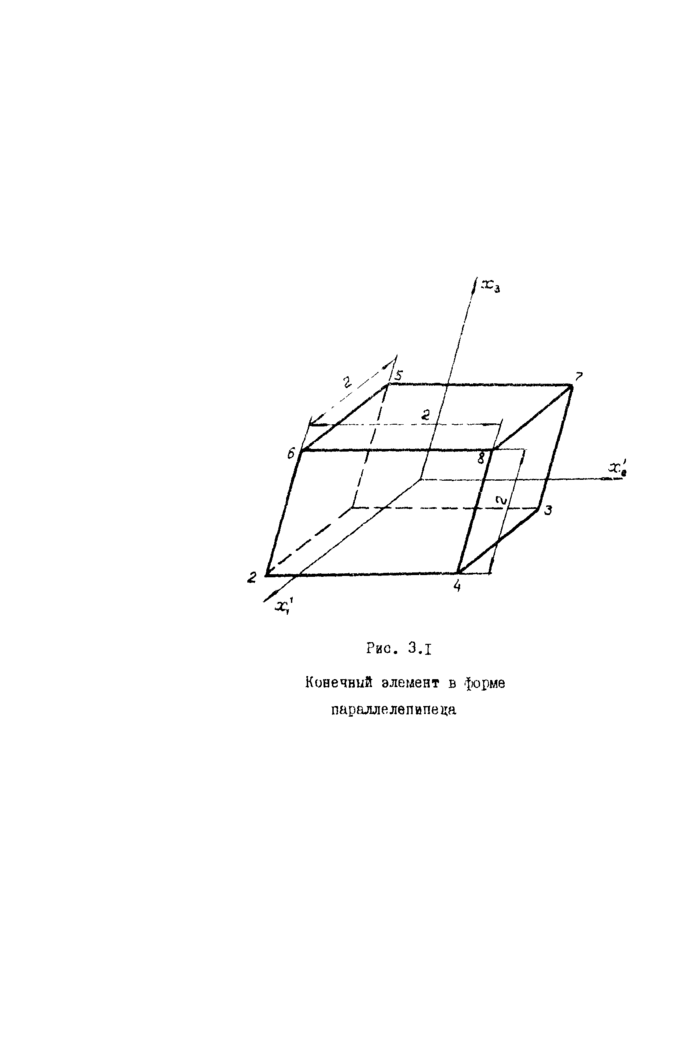
Конечннй элемент в форме коооугольного параллелештеда отобразим на куб о длиной ребра, равной 2. Местную онотему координат поместим в центр куба (рио.3.1). Перемещения точек КЭ предотавим вврахенкем
где
[Ят]г-[-ц-и-н~н];
[Рзт]Г^[Ч-4ЧЧНН];
т = 1,8 - яоквльннй номер уела.
Деформации еле ментов определяются по формулам
в, = / С?2 U” Pm (S+ ЯтХ*)(4+ Й>т X3);
fti- 4- cii и*йт(4+ OmX*)( 1 + й,тXs); f CXI и*'Рм(-?+ал>Х<)( 4 + втЯ*);
« да*/
= P & u* (* * Д,т&)(с?А» * cl'km);
UUi+&*&)(&'Am +C?Om);
) f ! С I / + Ptm X'XCl P3m + Cl Вт)
ff) " J
i
Рио. 3.1 Конечный элемент в форме
параллелепипеда
Группа T5I
РЕКОМЕНДАЦИИ
Расчета и испытания на прочность Метод конечных элементов и программы расчета на ЭВМ пространственных элементов конструкций в упругоплас-тической области деформирования
Р 50-54-42-88
ОКСТУ 4103
Рекомендации распространяются на расчет методом конечных элементов (МКЭ) пространственных объектов, подвергаемым статическим термосиловым нагрузкам при смешанных граничных условиях в упругопластической области деформирования.
Решение физически нелинейной задачи состоит в сведении краевой задачи к системе разрешающих нелинейных уравнений. Эффективность решения краевой задачи обеспечивается использованием моментной схемы конечных элементов ШСКЭ) [ 22J . При исследовании массивных и тонкостенных конструкций она не только превосходи^ другие варианты МКЭ, основанные на соотношениях теории упругости, но и не уступает оболочечным КЭ.
В рекомендациях предложен выбор оптимального алгоритма решения систем нелинейных уравнений, а также приведены г\лн определения точности получаемых результатов и затрп’ мо.инисто времени при использовании различных anr^ptrvon.
Матрица жесткости КЭ представляется в вхде
&] * Ес &*'j1
Коэффициенты матрицы хеотхоотх определяется по формулам
_ Г L pj/ Г'^
Ьтп ~ Ls it (Prnn 8
(по м и п - ее суммировать!), где
лТи --(1- s;)(i - &")(/-%)0-8Г)-.
I'-il-In-, ц] --[ir-cosm.,пУ]>-ъ ■
Можно существенно уменьшить количество операций при вычис-
/, S ь
дзнян коэффициентов Ьтп , если развернуть произведения х сум мы но воем индексам.
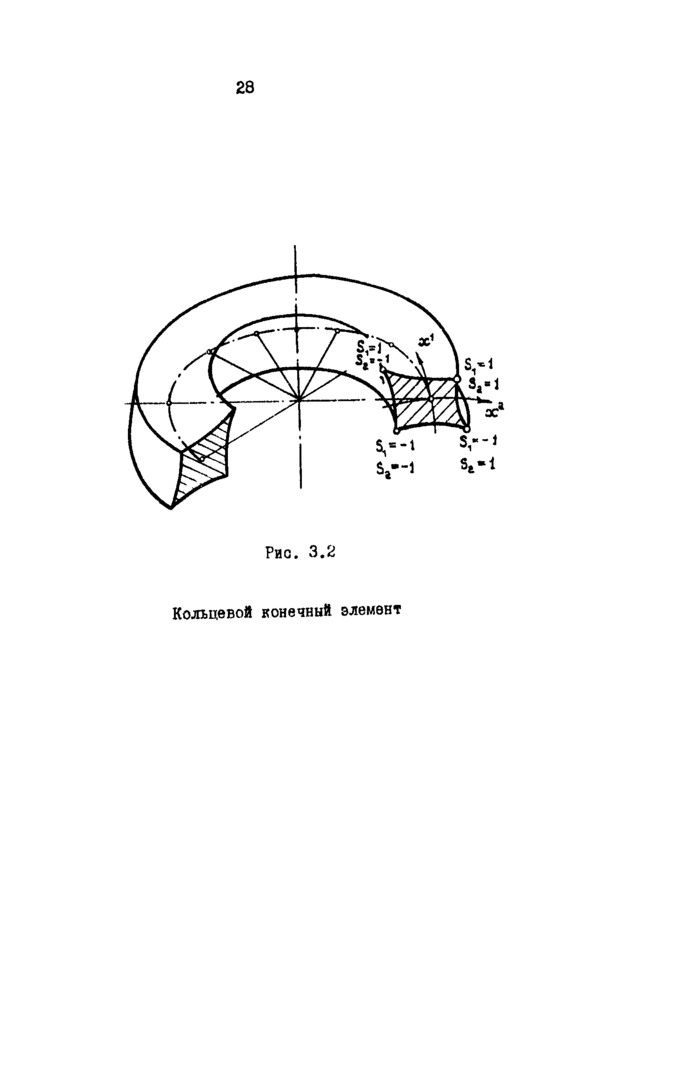
3.4. Иэопараметрический криволинейный КЗ Рассмотрим процесс вывода Ш для криволинейного параллели иинеда. Считаем, что область 0, занимаемая элементом (рно.3.1) отображена на куб о ребрами единичной длины, внутренние оьойсг
4
Эффективность решения пространственной задачи неосесим-матричного упругошгастического деформирования тел вращения обеспечивается применением полуакалитического метода конечных элементов (ПМКЭ), основанного на представлении перемещений и внешних нагрузок отрезками ряда ^рье по окружной координате и конечноэлементной аппроксимации их в плоскости меридианаль-ного сечения.
Метод конечных элементов реализован в пакете прикладных программ (ППП): "Куб"- для расчета пространственных тел призматической формы (общего вида) и "Круг" - для расчета неосесимметрично нагруженных тел вращения. ППП разработаны в развитие системы "Прочность-75", сданной в Республиканский фонд алгоритмов и программ \20] . Апробированы на контрольных примерах, показывающих эффективность метода и достоверность получаемых результатов при решении сложных задач упругопластического деформирования ответственных машиностроительных конструкций.
Подлинники программ хранятся в Киевском ордена Трудового Красного Знамени инженерно-строительном институте.
Рекомендации предназначены для специалистов НИИ, КБ и заводских лабораторий, занимающихся расчетами на прочность изделий машиностроения.
4a
I. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
Xе - местная система координат ZL‘ - базисная система координат
Ш - компоненты вектора перемещений в базисной сиотеме координат
ф - компоненты тензора деформаций в местной системе координат 6*J- компоненты тензора напряжений Si; - компоненты девиатора напряжений С( - компоненты тензора преобразования координат
- предел текучести при чистом сдвиге Т - температура
£ - параметр Одквиста Д коэффициенты Ламе
dr - коэффициент линейного теплового расвшрения Е - модуль упругости
- коэффициент Пуассона КЗ - конечный элемент
ПШ1 - пакет прикладных программ
MX - матрица жесткости
Щ - магнитный диск (том прямого доступа)
ВЗУ - внешние запоминающие устройства
АЦПУ - алфавитно-цифровое печатающее устройство.
5
2. ПОСТАНОВКА ЗАДАЧИ
2.1. Соотношения пространственной задачи термоупругости
2.1.1. Рассматривается напряженно-деформированное состояние трехмерного тела, которое занимает область $ , ограни
ченную границей Г . Физико-механические характеристики объекта изменяются произвольным образом внутри области S Тело деформируется под действием статически уравновешенной системы внешних сил и реакций связей,. Внешние воздействия могут быть представлены полем массовых внутренних сил, системой поверхностных нагрузок, приложенных на границе Г , и эквивалентными тепловыми нагрузками, вызванными неравномерным нагревом или охлаждением тела.
Важным классом пространственных задач термоупругооти являются тела вращения под действием неосесимметричного термооило-вого нагружения.
2.1.2. Для описания геометрии и граничных условий рассматриваемых объектов используется базисная система координат ZL . Внешние нагрузки и перемещение точек тела определяются проекциями в этой системе. Описание напряженно-деформированного состояния тел сложной формы упрощается в криволинейной системе координат , естественно связанной о геометрией тела. Такая система в дальнейшем называется местной.
2.1.3. Системы координат характеризуются компонентами метрических тензоров Qtj и Qtl/ , которые определяют масштабы базисных векторов и углы между ними. Символы Кристоффеля второго рода находятся по соответствующим компонентам Qtj и Qc)'
по формулам [ I ]
2.1,4. Полагается, что в любой точке тела известна связь между базисной и местной системами координат, осуществляемая тензором преобразования координат,
, if _ д21'
У “ ~ dxJ
Здесь и далее латинские буквы используются для обозначения индексов, принимающих значения 1,2,3, а греческие - 1,2.
2.1.5. Ковариантные компоненты метрического тензора в местной системе координат определяются через соответствующие компоненты в базисной
Ковариантные компоненты находятся по известным ковариент-
ным
7
fi ( Q'tj)
$
где - алгебраическое дополнение к элементу д-i/ мат
рицы, построенной по ковариантннм компонентам; g^d&iCgtjJ определитель этой матрицы.
+ Cl Uk'j - 2 Uк'■ Cl Cj fl'm ).
2.1.6. Принимается, что перемещения точек тела беоконечво малы. Тогда связь между компонентами тензора деформаций в местной системе координат и компонентами перемещений в базисной осуществляется в виде [i]
2.1.7. Для пространственных тел призматической формы в качестве базисной удобно использовать декартову систему координат В декартовых координатах не равны нулю следующие компоненты метрического тензора:
- дм - дм = f (2.6)
пк>
и вое li'm = 0. Компоненты метрического тензора в местной
системе координат определяются соотношениями
да -- Сс с]\ (2,7)
Связь между деформациями и перемещениями представляется в
виде
(2.8)
8
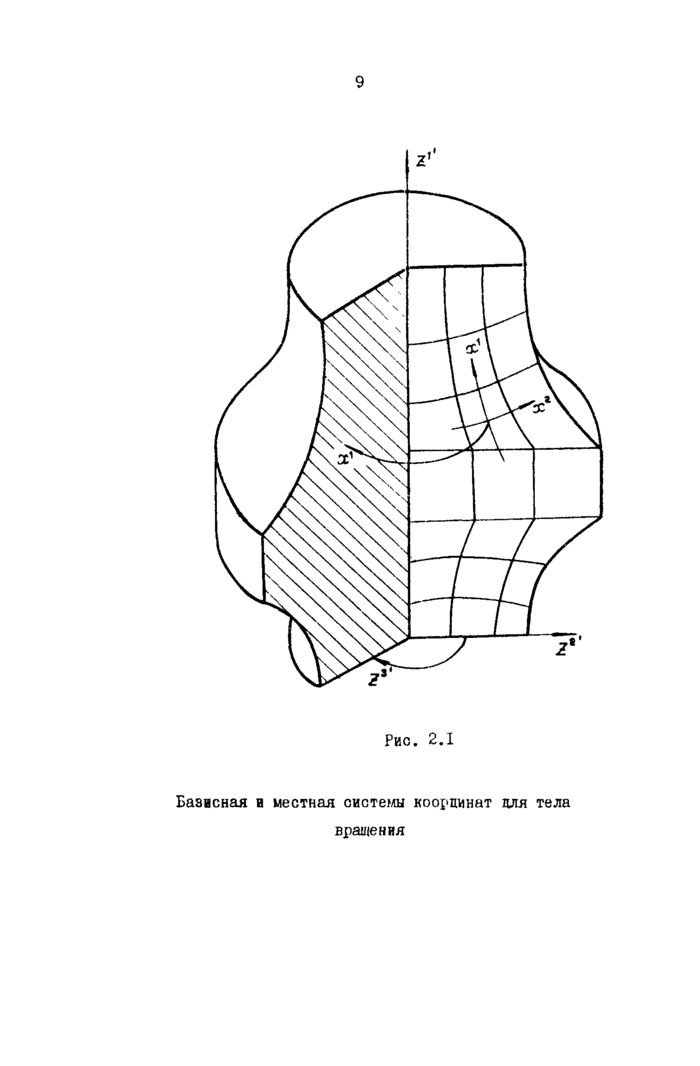
2,1.8. При исследовании тел вращения в качеотве базисной естественно принять круговую цилиндрическую систему координат (рно.2.1). В этом случае отличны от нуля; компоненты метрического тензора
9«-
символы Кристоффеля второго рода
пг' ryz' Н*'~ Г5‘- Х~
/5у = & ? 1з'£' " ‘2.'ъ' '%*’
Местная система координат Xе вводится таким образом, что
У 2
оси X и X расположены в плоскости меридионального сечения тела, а X6 совпадает по направлению с В9 . В силу ортогональности Хъ и В? к плоскости меридионального сечения имеем
cfi. (2ЛТ
С учетом выражений (2.9) и (2.II) компоненты метрического тензора в местной системе координат определяются соотношениями
Ск С ft Qrfr' •
gw
Связь между компонентами деформаций и перемещений осуществляется по формулам f ,
<4* = 7 (С<< fyfi * С/ь Щ* ) / ;
f - 4fи * ^)
t $ъ~ Uз'з V- Ul*
Базисная и местная системы координат для тела
вращения