ГИДРОПРОЕКТ ИМЕНИ С. Я. ЖУКА МИНЭНЕРГО СССР
РЕКОМЕНДАЦИИ по учету ползучести бетона при определении напряженно-деформированного состояния бетонных сооружений
П-795-83
Гидропроект
Москва — 1984
МИНИСТЕРСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФШСАЦИИ СССР
гмвнишроасг
Всесоюзный ордена Ленина проектно-изыскательский и научно-иоследоеательпкий институт "Гидропроект" имени С.Я.Жука
МУЧНО-ИХЩОВАТЕЯЬСКИП СЕКТОР (НИС Гидролроекта)
"УТВЕРЖДАЮ"
Главный инженер института
пГдоценко
"_"_,1983 г.
РЕКОМЕНДАЦИИ
ПО УЧЕТУ ПОЛЗУЧЕСТИ БЕТОНА ПРИ ОПРЕДЕЛЕНИИ КАПРЯНЕННО-ДЕЖСШИРОВАННОГО СОСТОЯНИЯ БЕТОННЫХ СООРУЖЕНИЙ
Е-795-83
Гидропроект
Зам.начальника НИСа Гидропроекта по научной работе, докт.техн.наук,
профессор /
Начальник отдела бетонных сооружений, канд.техн.наук
От.научн.еотр.,канд.тохн. наук
10
контуре сильно зависят от деформированного состояния тела, учет ползучести не может производиться с использованием принципа Вольтерра -Арутюняна [3] на ссноье упруго-мгновенных решений и требует полного решения краевой задачи с изменяющимися во времени характеристиками упругости и ползучести: совместное решение уравнений равновесия, неразрывности и физического уравнения состояния в форме
ч- • • foc.y,*)
f y(t) 3 ~^п7) "J dt
. ... ‘ \ . (х.у,л)
гдеetf v'Cqf+ttf)
В качестве приближенного метода решения таких сложных задач на практике может быть рекомендован шаговый метод решения краевой задачи, например, методом конечных элементов-с изменением на каждом шаге характеристик деформативнссти с учетом развития деформаций ползучести, отыскиваемых в соответствии с предисторией деформирования и нагружения.
3.
3.1. В расчетах конструкций с учетом старения и ползучести .
бетона (см.выражения(2.]), (2,используются:.
- функция полных удельных деформаций, равная
f c(t;d(зл)
и ко^^идиент Пуасоона полных деформаций
V ll,x)• const
II
3.2ч Модуль упругости, мера ползучести и коэффициент Пуассона, бетона определяются экспериментально при одноосном напряженном состоянии (как правило, при сжатии). Испытания должны производить-
|
и ГОСТ 24452-80 [Я .
3.3. Определение характеристик упругости и ползучести в отзетст |
|
ся на пароизолированных образцах по методике ГОСТ .24544-81 L 8 ]
тодом, предусматривающим испытания образцов, приготовленных из реального (производственного) состава бетона, либо элементов, выделенных и нагружаемых непосредственно в теле сооружений (как правило, при проведении натурных наблюдений за напруженным состояли* ем сооружения с помощью розеток телетензометров). Возможно также использование образцов бетона (кернов), отобранных па стройплоща--дке при их хранении в условиях полной пароизоляции.
3.4. Зависимость модуля упругости стареющего бетона от его возраста рекомендуется описывать в следующей форме
(3.3)
где Во ~ предельное значение модуля упругости бетона зрелого
возраста;
аД/п.а- коэффициенты, подбираемые по опытным данным.
3.5. Семейство экспериментальных кривых меры ползучести стареющего бетона рекомендуется описывать выражением, предложенным С.В,Александровским [ ll :
(3,4)
х) Сооружения I и П классов на стадии окончательного проектирования, строительства и эксплуатации.
12
где tyft) r A A) >
A t) - функции старения для предельных и быстронатекаялцкх
деформаций ползучести, которые рекомендуется описывать соответственно в форме:
Lf(r) * Lpo V феа'1+ ф c J*7г\ . фа
A(u* Ас * Ai2 4 Аг 2
(fo, А о - предельные значения функций lff[) и Л ft) ;
Ы, Ф-1 Ai,Axt jhjstjtfj* “ коэффициенты, подбирае
мые по опытным данным.
З.б. В случае, если по каким-либо причинам имеется только одна экспериментальная кривая меры ползучести, можно пользоваться методикой, предложенной С,В.Алексавдро^ским [^3 . Эта методика исходит из экспериментального факта,, показывающего, что при за-гружении бетона в различном возрасте до одинакового относительного уровня напряжений сжатия rl(f)~ (oft) !бп/^ ft) относительные
деформации ползуче сти
e(i,rc)ti(%) ■
га один и тот же интервал времени сказываются практически едина-новыми независимо от возраста бетона к моменту загружения. Исходя из кривей S(i t) и зависимости Pty> ft) можно получить полное семейство кривых меры.ползучести
sfi - с)1у7ы~ J (3-7)
котрое потом рекомендуется аппроксимировать по формуле (3.4).
3.7, Если длительность рассматриваемого воздействия составляет 2-3 года, для описания кривой меры ползучести бетона зрелого возраста рекомендуется использовать выражение, получаемое из фор-
му,та (3.4) путем предельного перехода:
£-(Ь~Т) “ .длительность воздействия*
3,0. В случае рассмотрения длительных воздействий, продолжающихся десятки лет, описание кривой меры ползучести бетона зрелого возраста должно осуществляться по формуле:
где:
1$, - предельное значение меры ползучести бетона при длительности воздействия нагрузки 2-3 года;
ГЦ - коэффициенты, подбираемые по опытным данным;
® '730 - 1100 сут. , длительность, дс которой возможно использование выражения (3.8).
Второй член з формуле (3.9) в логарифмическом масштабе по обеим осям вырождается в прямую линию. Эта формула применима ддл длительности действия нагрузки до 30 лет |*12,19,23] ,
3.9. Значения 0U и Гы в формуле (3,9) подбираются из условия наилучшего соответствия выражения
опытной хсривой меры ползучести бетона, зрелого возраста, полученной для данного сооружения в течение не менее 2-3 лет. Коэффициенты (Х\ и Гы определяются по выражениям
14
где h - произвольная длительность, равная приблизительно 30 суткам;
Oi - соответствующее значение меры ползучести.
ЗЛО. В случае, если имеются опытные данные по ползучести бетона при сложном напряженном состоянии, определение меры ползучести С(бЛ) и коэффициента Пуассона деформаций ползучести 1Л следует производить по выражениям:
(3.12)
_ Cge6(i;i) - Ccp(t,t)
се?&,г)
Сдеб ~ 4 *
_ б К - <Scf> С9еЬ - о* -СГ«у
>
. 6** 61*63
<3i + <5л
Указанная методика предусматривает независимое определение
двух деформационных характеристик материала непосредственно по
опытным данным при. трехосном напряженном состоянии общего вида
<о, ф <c?t Ф <oi , где <&’/, (os. 6U - главные напряжения.
„тт ■ ил)
З.П. В менее ответственных случаях определение характеристик упругости и ползучести может производиться методом аналогов с корректировкой при необходимости конечных значений меры ползучести в соответствии с известными рекомендациями по нормированию модуля
х) В случае, если какая-либо компонента девиатора напряжений близка к нулю, осреднение должно производиться по двум остальным ком
понентам.
хх) Сооружения 11!. ГУ класса на любой стадии и I и П ьарлтсльиых стадиях проектирования.
15
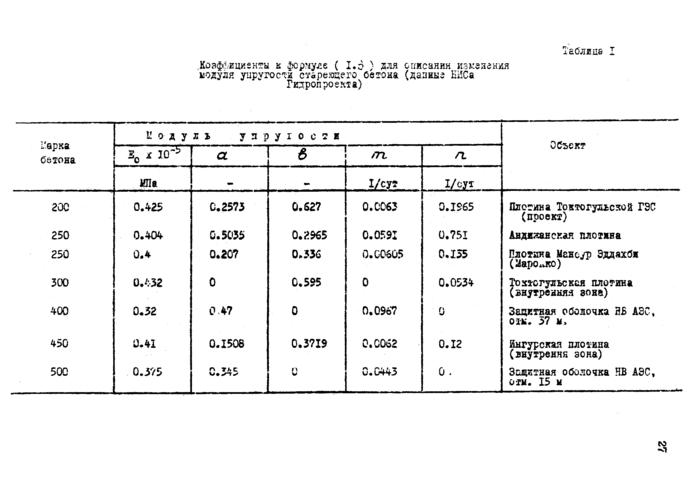
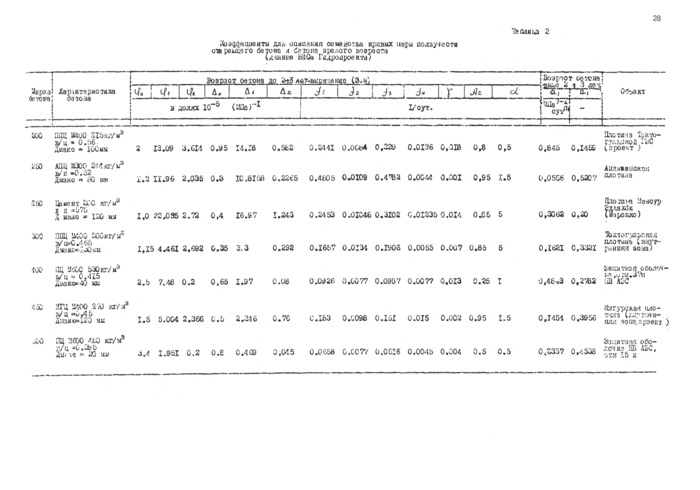
упругости ы и меры ползучести бетона [5,13,1б| . Для удобства
практического использования аналоговых данных й табл Л и 2 приложения I представлены численные значения констант в формулах (3.3)г~
(3,5)и (3.9) для ряда бетонов марок 200-500, применявшихся на конкретных энергетических объектах [lo] * При корректировке конечных значений мейы ползучести бетона с помощью методики нормирования [хб] поправочный множитель вводится только к величинам: сДъ До, At> Ал,
ЗЛ2. Для сооружений, длительное время эксплуатируемых при повышенной (до Ю0°С) температуре в условиях, обеспечивающих отсутствие заметных потерь влаги из бетона, его ползучесть и модуль упругости должны быть откорректированы на соответствующие условия.
В ответственных случаях такая-корректировка должна осуществляться по результатам специальных исследований ползучести рассматриваемого бетона & условиях повышенной температуры. В менее ответственных случаях в бетоне зрелого возраста корректировка может осуществляться по формулам;
С 7 = с *°L I ■* 0.03Н(г-20е')], (з Л4)ёт* ьсЮС / - о.о5 (т ■ го)], (2,15)
/*> ВО р Во
; С * с - мера ползучести и модуль упругости при
нормальной температуре 20°С);
С Г, Ь ‘ - то жз при повышенной температуре;
„ 7 - температура (средняя за длительный период) в °С. Приведенные зависимости относятся к случаю, когда сооружение начинает подвергаться повышенной температуре незадолго до начала
16
воздействия длительной нагрузки, так как не учитывают влияние повышенной температуры на процесс твердения (старения) бетона
[ш, 2?Г| .
ЗЛЗ. В бетоне раннего возраста, испытывающем воздействие экзотермического разогрева, влияние повышенной температуры на ползучесть и модель упругости бетона при расчетах термонапряженного состояния бетонной кладки в строительный период может не учитыватьс если максимальная температура бетона не превышает 40°С /дДб] .
В противном случае требуется такой*учет на основе специальных сксп$р?1ментально-теоретических исследований (V],
3.14, Расчет кривых релаксации напряжений K/> fitZ) рекомен дуется выполнять числонным методом по выражению [дЗ •
с fix. Ъ)+% Z‘3L , (3 1б)
д^‘)--5(и, Щ^У ЁрЩЩ)
t-r- - возраст бетона на момент отыскания напряжения!
Zi - фикси^юванйый возраст бетона в момент изменения напряжений. Модуль упругости и мера ползучести вводятся в расчет б виде выражений (3.3) - (3.5).
Для бетона старого возраста расчет кооффициентов релаксации может выполняться по формуле [z]:
г§е. А г- cTTj^~ l_(£tt+o>.A„)[Eoffy<,fo<A с) Vo j,A* - EcCf'y'o-tolAc)-Ai) fi.z ild +Eofp}>c +olA0) t i\lEo (ГФ'сю/afb + (ot.-j-У- Р£о(уу0 Ы Ло){о/~ I(“)J
17
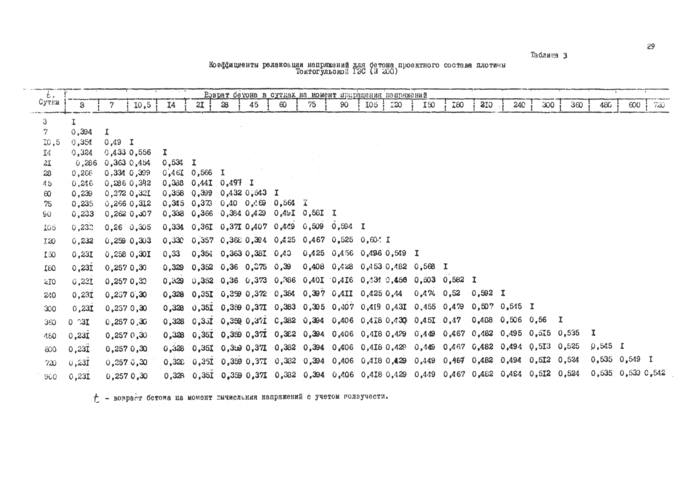
В приложении i (табл.3-5) приведены значения коэффициентов релаксации напряжений для бетона М20Г-450, которые могут использоваться в качестве аналоговых данных.
4. ПРОГРАММЫ ДЛЯ УЧЕТА ПОЛЗУЧЕСТИ БЕТОНА В ПРАКТИКЕ ИНЖБНЕРНЫХ РАСЧЕТОВ НА Ш
4.1. Дм автоматизации обработки экспериментальны:: данных
и расчетов напряженного состояния предлагаются программ, разработанные для ЭВМ БЭСМ-6. Программы написаны на языках АЮЛ и Фортран, сданы в фонд алгоритмов и программ НИСа Гидропроекта. Алгоритмы, тексты программ и инструкции по их использованию приведены в приложениях 2-6.
4.2. Аппроксимация зависимости модуля упругости от возраста бетона в форме (3.3) выполняется по программе АППРЕ (приложение 2). Программа позволяет получать значения коэффициентов, входящих в формулу (3.3), и предельное значение модуля упругости бетона. Могут быть рассчитаны значения модуля упругости на любые заданные моменты времени.
4.3. Аппроксимацию экспериментальных кривых меры ползучести рекомендуется выполнять по формулам (3.4),$,5) с помощью программы АКРИЛ (приложение 3), которая позволяет определять значения коэффициентов и функций, входящих в нее, на базе метода наименьших квадратов с использованием всех экспериментальных точек. Подобная аппроксимация, рыполнявшая-ся ранее на базе ручных расчэтов, из-за своей трудоемкости не позволяла отыскивать оптимальное- сочетание указанных коэффициентов, что делало эту процедуру неточной.
После подбора коэффициентов в программе производится вычисление значений C(tX) для исходных по опытам значений Т , что дает
18
возможность легко контролировать результаты аппроксимации.
Программа АКРИЛ позволяет расчитать значения C(t,t) для любых значений t и Z , что необходи- о при расчетах напряженного состояния с учетом ползучести численными методами.
4.4. Для расчета меры ползу тести без предварительной аппроксимации по имеющимся значениям коэффициентов в формуле (З.Ч ) может использоваться программа МЕР.ШЗ (приложение 4).
4.5. Для расчета кривых релаксации напряжений tCpfl.'t) по формулам (3.1(5-0.17) рекомендуется программа РЕЛАНП (приложение 5), в которой осуществлена численная реализация процедуры перехода от Cft Л) к tyftft). При этом учитывается также переменный модуль упругости ботона Е(т) . В программе ИЯАЖ предусмотрен также расчет Kj)(i‘T.) для бетона старого возраста по формуле (3.17). В целом программа РДЛАКС позволяет рассчитывать неограниченное число кривых релаксации, что дает возможность на практике широко пользоваться простым инженерным методом учета ползучести бетона на основе упругих решений краевых задач*
4.6. Напряжения с учетом ползучести Жетона по заданным в данной точке полным деформациям позволяет рассчитать программа НАЛ? (приложение 6), ксторая использует меру ползучести з форме (3.4)
и модуль упругости в виде (3.3). Алгоритм программы разработан на основе метода Й.В.Швецова [I?J ,
В качестве исходных даштых кроме деформаций на определенные моменты ьременч „вдаются значения коэффициентов, входящих в зависимости (3.3)01,5). Если известны упруго-мгновендае напряжения для ряда моментов времени, то они делятся на значения модуля упругости для тех же моментов времени и полученные деформации вводятся з программу в качестве исходных ( заданных ) деформаций.
19
Программа мс*еет быть использована для обработки результатов экспериментов, ь которых замерены полные (длительные) деформации бетона, в том числе и для обсчета натурных наблюдений за состоянием сооружений с помощью розеток телетензометроз. В этом случае заданные деформгщии определяются по формуле (2.3). Свободные температурно-влажностные деформации при этом должны быть исключены (например, с помощью измерения деформаций в ненапряженных элементах - "усадочных конусах").
4.7. Программа НАПР относится непосредственно к одномерной задаче теории упруго-ползучего тела, но может использоваться также в общем случае трехмерного поля напряжений, если известны три ортогональные компоненты тензора полных деформаций. Б этом случае по выражению (2.3) вычисляются "приведенные" деформации по каждой оси, а процедура вычислений напряжений остается прежней. Здесь как и обычно п теории ползучести используется соотношение (3.2), что предполагает задание еще одной константы - коэффициента Пуассона.
4®8® Программа ШЛР может щшмевяпоя ж в чисто расчетных задачах для однородной облаем® Здесь может встречаться ряд случаев* Воле граничные условия заданы только в вида усилий (напряжений), то в линейной области решение в напряжениях о учетом ползучести в точности равно решению упруго-мгновенной задачи,а перемещения а любой точке изменяются во времени в соответствии с изменением меры ползучести* В этом случае учет ползучести для напряжений не требуется*
Вели задача связана с воздействием кваяистшдионарньгх шттуж-денных деформаций (температура, усадке, осадка спор и т.гп). а условия на контуре заданы в виде свободного или жестко защемленного края, то полные деформации будут постоянными во времени и могут
го
быть найдены из упругого решения краевой задачи. Подставляя найденные таким образом деформации в программу НАИР в виде временного ряда значений для каждой точки отдельно, мы в итоге получим затухание напряжений за счет ползучести бетоне. Это затухание зависит от истории заданных воздействий.
D общем более сложном случао, когда граничные условия не ссвпадают с огшсашьши выше ( упруго-податливая опора и т.д.), или если речь идет о контактной задаче теории ползучести (кусочно-однородное упруго-ползучее тело) расчеты напряжений с учетом ползучести треб^тот более общего подхода, не связанного с принципом Волътерра-Арутдаяна [з] . Подобное положенно в общем случае имеет место и в нелинейной области ползучести. Во всех этих случаях программа HAPJP может Сыть использована только для приближенных решений,
,.9. Расчет потерь предварительного напряжения вследствие ползучести бетона по методике А.В.Швецовз [l8^B центрально обжатых железобетонных элементах сводится к решению интегрального уравнения теории ползучести по программе HAIIF при следующих дополнительных указаниях: усадочные деформации принимаются нулевыми;
- вычисляется параметр армирования
<*.!)
где с,Л/л- коэффициент обычного армирования,
Си. - модуль упругости обычной арматуры,
JU«,£n - то ке для предварительно напряженной арматуры;
- вычисляются значения деформаций ползучести- бетоне от постоянного
(условно) предварительного напряжения бь(Т^)\ приложенного цеят-ралхяо ь возраста бетона Т*
(4.2)
3
ПРЗДИСШОШШ
В связи с расширением области применения бетоне и желвзо-бетоиа аа Последние годы появилось иного новых исследований, посвященных вопросу ползучести бетона в условиях повышенной тейпе ратуры и сложного напряженного состояния, характерных для внже-нериых сооружений энергетических объектов. В то же время в связи с использованной ЭВ1£ увеличилась надежность расчетного прогнозирования напрялоиного состояния сложных сооружений, в том числе простраиствонно-работалщих. Поскольку большинство сооружений энергетических объектов рассчитано на длительную эксплуатацию в течение 30 и более лет, учет длительных процессов, связанных с ползучестью бетона, приобретает важное значение.
В настоящей методической работе на основе анализа и обобщения экспериментальных данных по ползучести бетона, полученных за последние годы, разработаны рекомендации по учету ползучести бетона в практике расчетов и натурных исследований бетонных сооружений.
Среди новых факторов ччтены результаты исследований последних лет, касающиеся сложного напряженного состояния, влияния повышенной температуры и длительного срока зкеплуатацин сооружений. В качестве аналогов представлены данные по ползучести бетона ряда крупных энергетических объектов, бетон которых исследовался в «а-туре или на крупномасштабных образцах.
Рекомендации предназначены для использования в практике проектирования, расчетов и натурных исследований бетонных и железобетонных конструкций энергетических сооружений.
Работа выполнена в отделе бетонных сооружений в рамках задания по теме 0.55.08.О?.HI.
В разработке Рекомендаций принимали участие:каид.тех». наук Мгалобелов Ю.Б., каад.тех»-наук Коган Е.А., инж.Соловьева Л.Д.
ч
ПЕРЕЧЩЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
напряжения с учетом ползучести на момент времени t ,
- напряжения упруго-мгновзнной задачи,
зал) - полные удельные продольные деформации в
условиях одноосного напряженного состояния,
<Ш) - полние удельные поперечные деформации, в тех же условиях,
Ол(гХ) » полные удельные деформации чистого сдвига,
£ - время; возраст бетона на рассматривавши момент,
(t.'t) - длительность действия нагрузки.
fcpfit'l)" коэффициент релаксации напряжений,
СМ" мера ползучести бетона, ф) - модуль упругости,
Gti) - модуль сдвига,
4,t)- коэффициент Пуассона полных деформаций,
коэффициент Пуассона упругих деформаций,
коэффициент Пуассона деформаций ползучести,
- компоненты тензора полных деформаций,
К - модуль средних (объемных) деформаций,
модуль девиаторных деформаций,
Одеб ~ компоненты девиатора полных удельных деформаций,
5
дер - мера полных ,средних1 (объемных) деформаций, CgeuftiT) - компоненты девиатора деформаций ползучести, Cep ft, Т) - мера- средних (объемных) деформаций ползучести.
6
I. ОБЩИЕ УКАЗАНИЯ
I Л.Настоящие рекомендации относятся к случаям определения нащ^яженно-деформированного состояния массивных либо изолирован-ных от высыхания бетонных^трещиностойкюс и предварительно напряжен иых железобетонных конструкций энергетических соор./жений, подвер гающихс'1 длительным воздействиям.
1.2. Рекомендации распространяются как на случай расчетного определения напряженно-деформированного состояния методами линей ной теории ползучести, так и на случай экспериментгигьного определения напряжений в сооружениях тензометрическим методом (включая натурные исследования).
1.3. В диапазоне напряжений от предела длительной прочности при растяжении 0,8,0. р) до 0,5R пр яри однооснсм сжатии, а в случае двух- и трехосного сжатия до 0,6 Rnp учет ползучести бетона может производиться по линейной теории ползучести. В тех случаях, когда напряжения в эксплуатационный период превышают указанные пределы, необходим переход на нелинейную теорию ползучести с использованием рекомендаций работы [is! . В данной работе вопросы нелинейной ползучести ке рассматриваются.
1.4. В случае двутг и трехосного напряженного состояния, как показывает анализ экспериментальных данных [il,19-22, 2/ф~2б] * деформационные характеристики: модуль ущгтости, мера ползучести, коэффициент Пуассона могут приниматься независимы?^ от вида калря -женаэго еостсяни: и определяться по результатам одноосных испытаний.
Указанное положение имеет место в области линейной ползучее т (при трехосном сжатии 6>^0,6 Rnp), В этих условиях деформирование происходит в соответствии с обычным принципом суперпозиций,
7
что позволяет применять на практике выражения» основанные на обобщенном законе Гука для упругой деформации и т подобные для деформаций» разбивающихся во времени.
2, ОСНОВНЫЕ РАСЧЕТНЫЕ ПОЛСЖШШ
2Л. При расчете конструкций или сооружений» для которых важно знать развитие напряжений с учетом собственных (технологических, темперагурно-усадочных и т.пЛ напряжений, появляющихся,, как правило, с раннего возраста бетона, необходимо применять теорию упруго-ползучего тела в ее современном модифицированном варианте [Д*3,4_].
При расчете напряженного состояния сооружений от длительных нагрузок и воздействий, прикладываемых з зрелом возрасте бетона» рекомендуется использовать теорию упругой наследственности, которая эквивалентна теории упруго-ползучего тела с инвариантны^^ во времени свойствами упругости и ползучестиг,[1,41 „
2.2. В целом ряде практических случаев: обработка данных натурных наблюдений, обсчет результатов измерений деформаций в экспериментах, расчеты для однородных тлл при действии вынужденных деформаций температурно-усадочного характера* расчет потерь пред-напряжений и т.п. учет ползучести бетона должен производиться с помощью интегрального преобразования
6к it) = <$К (О+ t[t)J <оШ -щ dill's drC} > г Л)
основанного на принципе Вольтерра - Арутюняна [о] и использующего понятие о напряжениях упруго-мгновенной задачи Со к ( ij -
6s(i)' Е({:) , где: (бк t £ к - компоненты тензора напряже
ний и деформаций.
8
2*3. В случае расчетного определения напряженного состояния у пруто-мгновенные напряжения ^находятся для последовательного ряда моментов времени на основе решения кваэистатических задач теории упругости. В случае натурных исследований упруго-мгновенные напряжения равны
(2.2)
-..............(x,y, A ),
(x,y*£ ) - обозначает круговую замену индексов для остальных компонентов тензора напряжений;
6у, 6». - измеренные компоненты полных деформаций по трем взаимно ортогональным осям;
V - коэффициент Пуассона.
2.4. Выражения (2.1) - (2.3) относятся к нормальным напряжениям, для касательных напряжений они остаются аналогичными с заменой:
6(t,l) на 6k(ipi)'Z(^v)6(t;i))Eft) на Gft) ~ n(i^) - €** на f*i
Касательные напряжения упруго-мгновенной задачи равны;
%rl(t)* Gft)
2.5. При разложении тензора напряжений на шаровую (среднюю) и девиаторную составляющие учет ползучести производится по выражению вида (2.1) с использованием соответствующих составляющих тензора напряжений с учетом ползучести и тензора упруго-мгновенных
напряжений, а также с заменой Eft) и (jfi'l) функции удельных средних и девиаторных деформаций:
6t/>(bfcO-M)d(t,Xh Sgiskrc) ■ fav)б(ьл) (2.5)
Коэффициент Пуассона V в этих случаях может быть принят одинаковым для упругих и полных деформаций и постоянным во времени. При отсут ствии опытных данных рекомендуется среднее для бетона значение V -0.2.
2.6. Для инженерных расчетов в упрощенной форме учет ползучести бетона налет производиться также с помощью коэффициентов релаксации напряжений Kp(t,'t} методом "ступенек" £б ] :
t-
6%) «Cottyfik) t^l Л <oj Кр (t, ), ( 2.6)
с £/*" 4 * £ j где ^j -—a^ * середина временного шага;
<£/*<?/?/) El'ZV) - упругие напряжения в начальный момент времени Tt , с которого начинается рассмотрение задачи;
А (од - приращение упруигх напряжений, вычисленных без учета ползучести, но с учетом переменного во времени модуля упругости.
Б случае обработки натурдах измерений они равны: .
Метод коэффициентов релаксации рекомендуется применять, в основном, для решения задач о термонапряженном состоянии массивных бетонных сооружений,
2.7, В тех случах, когда решение задачи с учетом ползучести производится доя существенно неоднородного тела с различными сбой-ствами упругости и ползучести или когда граничные условия на