ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
ГОСУДАРСТВЕННАЯ СЛУЖБА СТАНДАРТНЫХ СПРАВОЧНЫХ ДАННЫХ (ГСССД)
УДК 547.216:536.7
ТАБЛИЦЫ СТАНДАРТНЫХ СПРАВОЧНЫХ ДАННЫХ
Н-ПЕНТАН. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА В ДИАПАЗОНЕ ТЕМПЕРАТУРЫ ОТ ТРОЙНОЙ ТОЧКИ ДО 700 К ПРИ ДАВЛЕНИЯХ ДО 100 МПа
ГСССД 291 -2013
Москва-2013
РАЗРАБОТАНЫ ФГУП «СТАНДАРТИНФОРМ» с участием специалистов ООО «ГАЗПРОМ ВНИИГАЗ» докт. техн. наук Григорьева Б. А. и ФГБОУ ВПО «Калининградского государственного технического университета» докт. техн. наук Герасимова А. А, канд. техн. наук Александрова И. С.
ОДОБРЕНЫ экспертной комиссией в составе:
д-ра техн. наук А. Ф. Богатырева, д-ра техн. наук М.И. Лсвинбука, канд. физ.-мат. наук Е. Е. Городецкого, канд. техн. наук. Ю. В. Мамонова.
ПОДГОТОВЛЕНЫ к утверждению Российским научно-техническим центром информации по стандартизации, метрологии и оценке соответствия (ФГУП «СТАНДАРТИНФОРМ»)
У ТВЕРЖДЕНЫ Федеральным агентством по техническому регулированию и метрологии «31» октября 2013 г. (протокол № 3)
2
В используемом алгоритме используется аддитивный критерий оптимальности - минимизируемый функционал (15), который образуется путем сложения выходных параметров, преобразованных к безразмерным слагаемым. Это осуществляется с помощью введения нормирующих множителей -весовых коэффициентов. Нормирование необходимо для объединения нескольких выходных параметров - термодинамических свойств, имеющих в общем случае различную физическую размерность. Минимизируемый функционал содержит слагаемые, ответственные за точность аппроксимации результатов измерений разнородных данных о термодинамических свойствах, а также различные ограничения, накладываемые в виде неравенств на термодинамическую поверхность и представлен следующей зависимостью:
(АЗ)
где: Ж-весовой коэффициент для каждой опытной точки, /'- функция, используемая для минимизации отклонений. Например, для изохорной теплоемкости данных функция определяется как:
(А4)
Квадратичные функции для других термодинамических свойств имеют аналогичный вид. F0 функция, учитывающая различные ограничения на область изменения переменных.
Весовой коэффициент W для каждой выбранной опытной точки назначался индивидуально с учетом типа данных, области состояний и требуемой точности. Типичное значение W для р,р,Т- данных и давления насыщенных паров составляет I, для теплоемкости - 0,5, для скорости звука - 1.
Как видно из соотношения (АЗ) ограничения входят в виде дополнительных слагаемых в минимизируемый функционал. Например, для контроля знака производной какой-либо термодинамической величины численно вычисляется производная на основе расчетных значений по уравнению состояния, сохраненных на последних итерациях. После этого вычисленное значение производной по соответствующему свойству в безразмерном виде с соответствующим весовым коэффициентом включается в квадратичный функционал со знаком противоположным заданному. Замена знака на противоположный осуществляется для того, чтобы при правильном знаке производной это ограничение не влияло на функционал (АЗ).
Ограничения не влияют на критерий оптимальности до тех пор, пока параметры находятся в области допустимых значений. Стоит изменить параметр таким образом, что он пересечет границу, движение по траектории минимизации немедленно прекращается. Эта процедура продолжается плоть до возвращения параметров в область допустимых значений. Блок-схема алгоритма представлена на рисунке А1.
На шаге 1 задается количество итераций, задается точность, с которой ищется минимум и начальное приближение.
На шаге 2 осуществляется вычисление функционала в новой точке пространства поиска и добавление ограничений (шаг 2А). Это осуществляется
11
изменением начальных значений переменных в соответствии с заданным шагом поиска по следующей итерационной формуле
(А5)
где [хк] - массив начальных значений переменных, (xk+il - массив значений переменных на новой итерации, лК - шаг поиска на £-ой итерации.
После этого вычисляется значение функционала (АЗ) в новой точке пространства поиска S(xk+i). В качестве начальных значений переменных могут выступать коэффициенты уравнения состояния, либо коэффициенты и показатели степени при температуре и плотности одновременно. Величина шага поиска возвращается генератором случайных чисел и может варьироваться в диапазоне 10''<А.< 10'7.
На шаге 3 производится сравнение значений минимизируемого функционала на текущей и предыдущей итерациях. Если S(xk+i) < S(xk), то осуществляется переход к шагу 4. В противном случае на шаге ЗА запускается счетчик неудачных попыток и так же осуществляется переход к шагу 4. Если предельное количество неудачных попыток достигло максимума, то осуществляется выход из программы. Негативные шаги необходимы для того, чтобы избежать ловушки локального оптимума.
На шаге 4 информация о поведении минимизируемого функционала, накопленная в процессе поиска, используется для дробления шага поиска
К
где а е (-1, I) - коэффициент уменьшения шага (свободный параметр метода).
Параметр а в процессе дробления шага поиска изменяется следующим образом. При сравнении предыдущего и текущего значений функционала, алгоритм выбирает направление поиска и в соответствии с этим направлением определяет первоначальное значение коэффициента а
(Л7)
то есть принимается решение об увеличении, либо об уменьшении шага поиска. После присваивания коэффициенту а соответствующих значений по условию (А7) вычисляется новое значение функционала Л* /. Далее осуществляется дробление шага поиска изменением коэффициента а исходя из следующих условий
12
Если ни одно из группы условий (А8) не выполняется, то для определения нового значения а строится интерполяционная парабола на основе значений минимизируемого функционала S и коэффициента « на последних трех итерациях. Для этого используются следующие соотношения
= _S*., х(яг,+| -ак) + х(ак -ak_t) + S*x(а*_, -ам)
(«*♦1 -«*)*(**- ак-\)х (<**-. - ам)
где а и h - коэффициенты параболического уравнения. Тогда новое значение коэффициента а определяется как
Далее после вычисления нового значение функционала в соответствии с новым значением коэффициента уменьшения шага, сохраняются три наилучших значения функционала S и коэффициента а и алгоритм переходит к шагу
5.
На шаге 5 проверяются условия останова. Программа завершает свою работу, если достигнуто максимальное значение неудачных попыток минимизировать функцию или достигнута требуемая точность решения
где f.s- константа, определяющая требуемую точность решения по S.
Если ни одно из условий останова не выполнено, то осуществляется переход к шагу 6, на котором переопределяются границы поиска в соответствии с новыми значениями переменных, предыдущему значению функционала присваивается текущее значение, и алгоритм переходит к следующей итерации.
Таким образом, осуществляется цикл поиска глобального оптимума для разрабатываемого уравнения с учетом заданного количества итераций.
Кроме определения коэффициентов и степеней уравнений состояния, посредством вышеописанного алгоритма определено оптимальное количество слагаемых уравнения, удалением тех из них, которые вносят минимальный вклад. Это осуществляется поочередным приравниванием каждого сла-
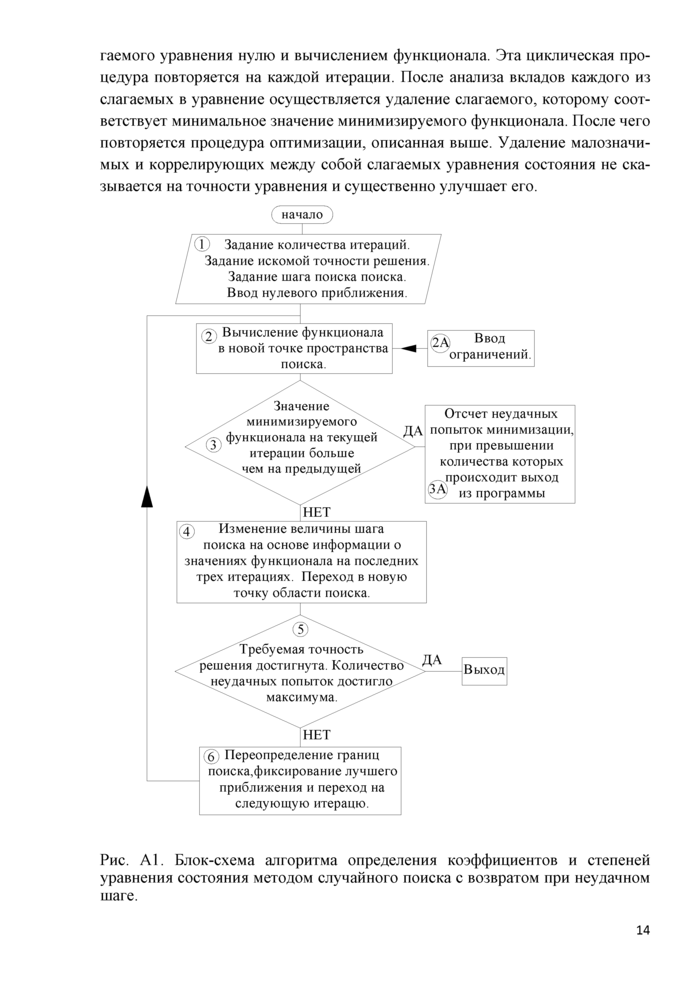
гаемого уравнения нулю и вычислением функционала. Эта циклическая процедура повторяется на каждой итерации. После анализа вкладов каждого из слагаемых в уравнение осуществляется удаление слагаемого, которому соответствует минимальное значение минимизируемого функционала. После чего повторяется процедура оптимизации, описанная выше. Удаление малозначимых и коррелирующих между собой слагаемых уравнения состояния не сказывается на точности уравнения и существенно улучшает его.
Рис. А1. Блок-схема алгоритма определения коэффициентов и степеней уравнения состояния методом случайного поиска с возвратом при неудачном шаге.
14
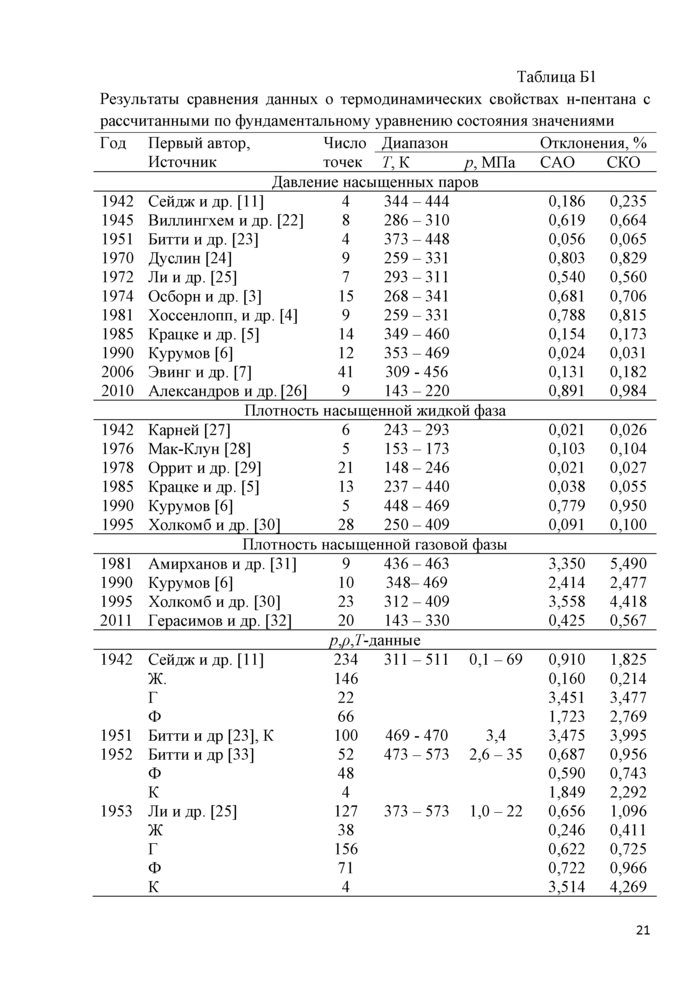
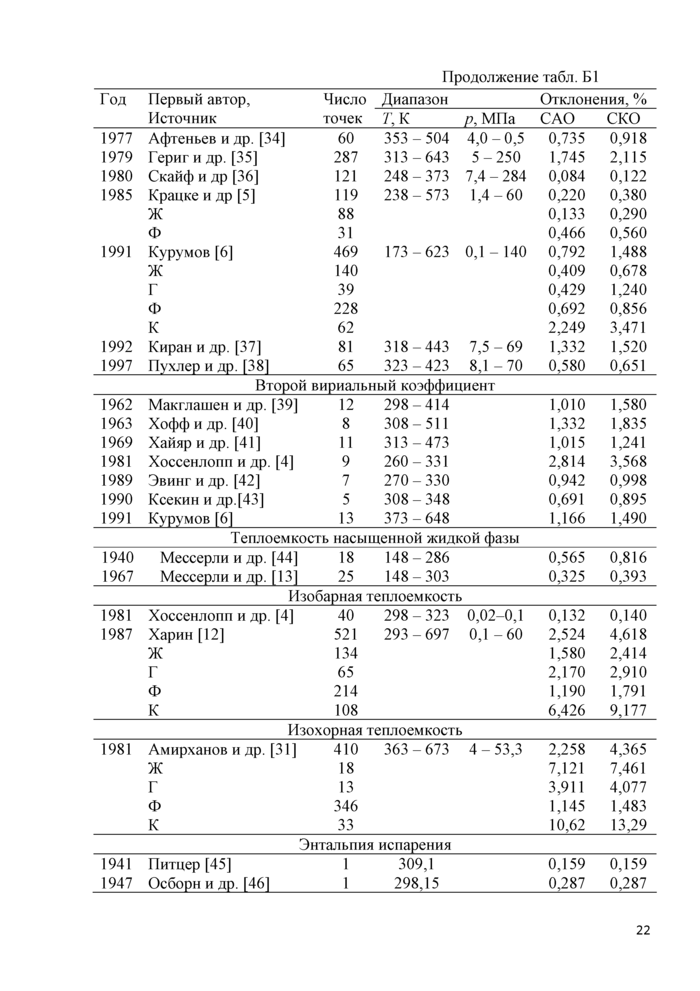
ПРИЛОЖЕНИЕ Б Анализ результатов и оценка точности табличных значений ТДС
Термодинамические свойства н-пентана исследованы весьма подробно и в широком диапазоне парметров состояния. Однако вся предыдущая история разработки УС н-пентана свидетельствует о не слишком хорошей согласованности данных о термических свойствах, в частности /?,р,7-данных. Такая ситуация, на наш взгляд, объясняется промежуточным положением н-пентана между газом и жидкостью (нормальная температура кипения н-пентана чуть выше комнатной). Поэтому, используя экспериментальные установки, разработанные для жидкостей, экспериментаторы неизбежно вносят дополнительные трудно исключаемые погрешности, связанные с высокой летучестью вещества. Достаточно подробный обзор экспериментальных данных и уравнений состояния, полученных до 1987 года, представлен в [18]. Анализируя, представленные в [18] результаты можно сделать вывод, что на тот момент были разработаны различные уравнения состояния, описывающие термодинамические свойства в той или иной области с различной погрешностью. Однако, несмотря на весьма большой объем экспериментальных данных, отсутствовало фундаментальное уравнение состояния (ФУС), которое описывало бы все термодинамические свойства с погрешностью, близкой к экспериментальной, в диапазоне температуры от тройной точки до начала термической диссоциации н-пентана (~ 700 К).
Среди наиболее поздних исследований, посвященных разработке ФУС, следует выделить работу' Ратанаписит и Эли [19], в которой получено модифицированное 32-х константное уравнение состояния Бенедикта - Вебба -Рубина, работу' Спана [16], в которой фундаментальное уравнение, описывающее безразмерную свободную энергию Гельмгольца, представлено оптимизированным 12-ти константным уравнением и работу Сона и Эли [20], в которой предлагается оптимизированное, единое для полярных и неполярных веществ 14-ти константное ФУС. Уравнение Ротанаписит и Эли [19] применимо в диапазоне температуры 173 - 573 К, а уравнения Спана [16] и Сона и Эли - в диапазоне температуры [20] от тройной точки до 573 К.
Как показал наш анализ, уравнение Спана [16] является наиболее точным, описывающим с погрешностью, близкой к погрешности эксперимента, все термодинамические свойства в диапазоне температуры от тройной точки до 600 К. Это уравнение включено в известную базу данных REFPROP [21].
Представленное в данной работе ФУС получено на более обширном экспериментальном материале и, благодаря своей структуре, обеспечивает
15
более высокую точность расчета ТДС в критической области (0,7 < р/рс< 1,3 и 0,98 < 777’с < 1,1), а также обоснованно может применяться до 700 К.
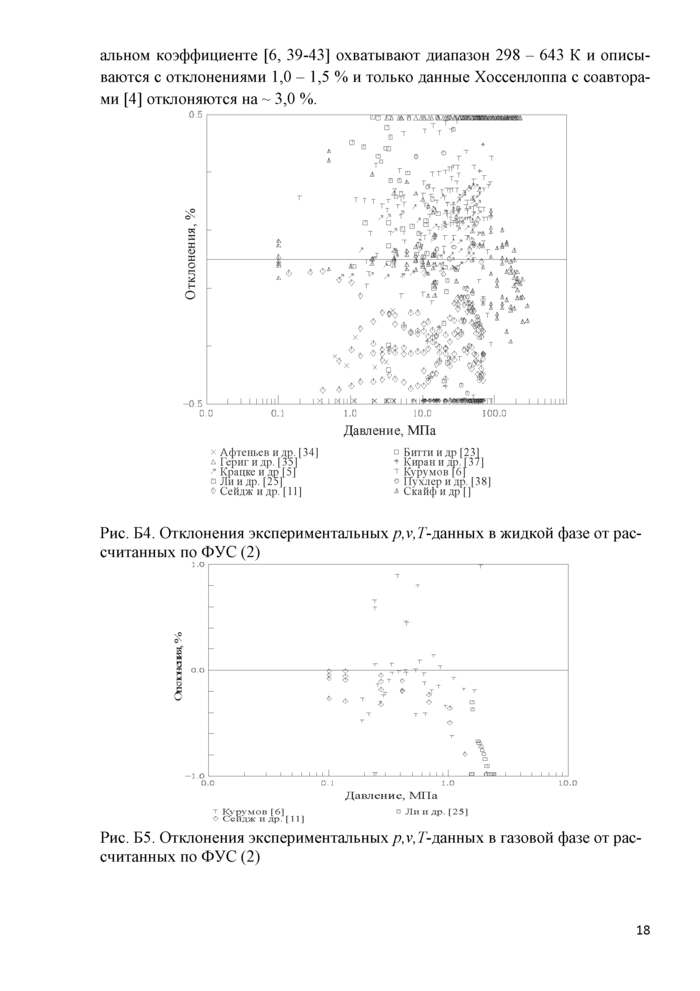
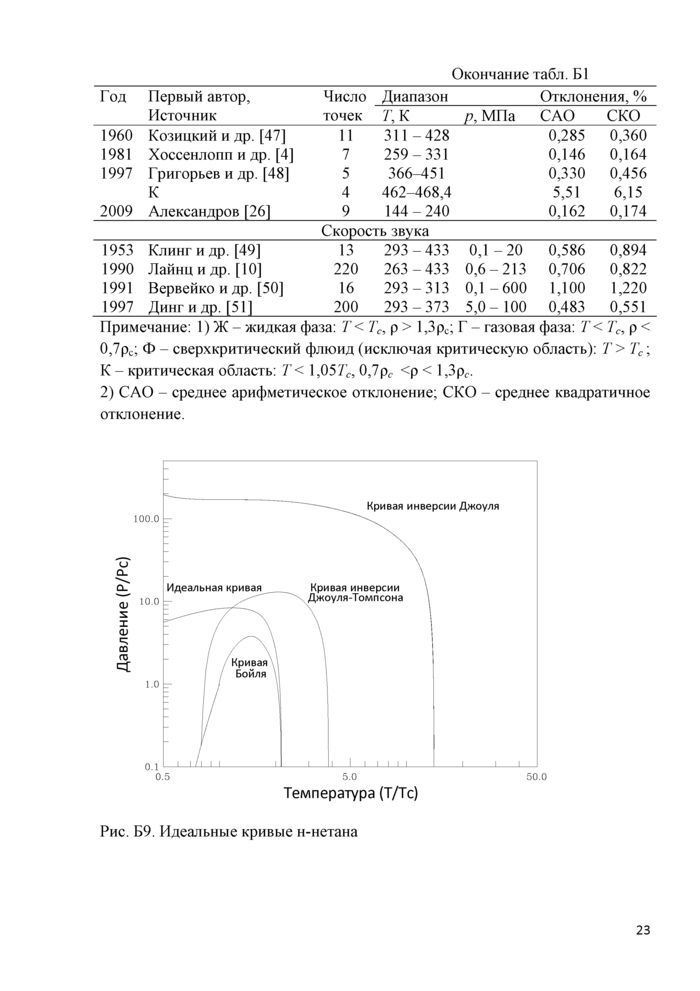
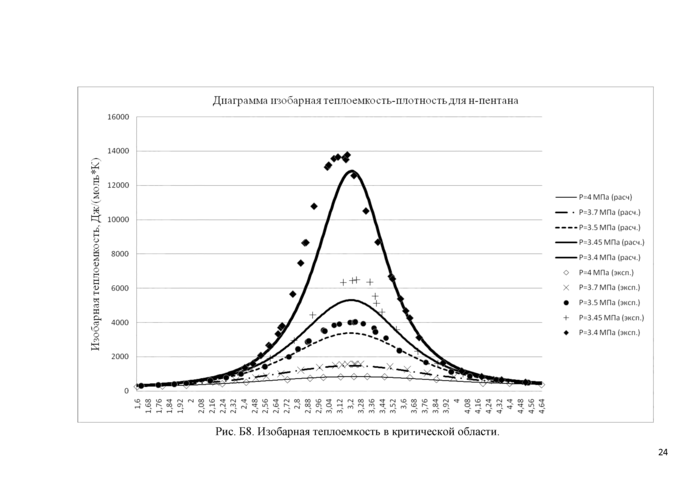
В табл. Б.1 и на рис. Б.1 - Б.8 представлены результаты сравнения экспериментальных данных о ТДС н-пентана с рассчитанными по ФУС (3) значениями. Следует иметь ввиду, что при определении коэффициентов ФУС, использовались только те данные, которые хорошо согласуются между собой.
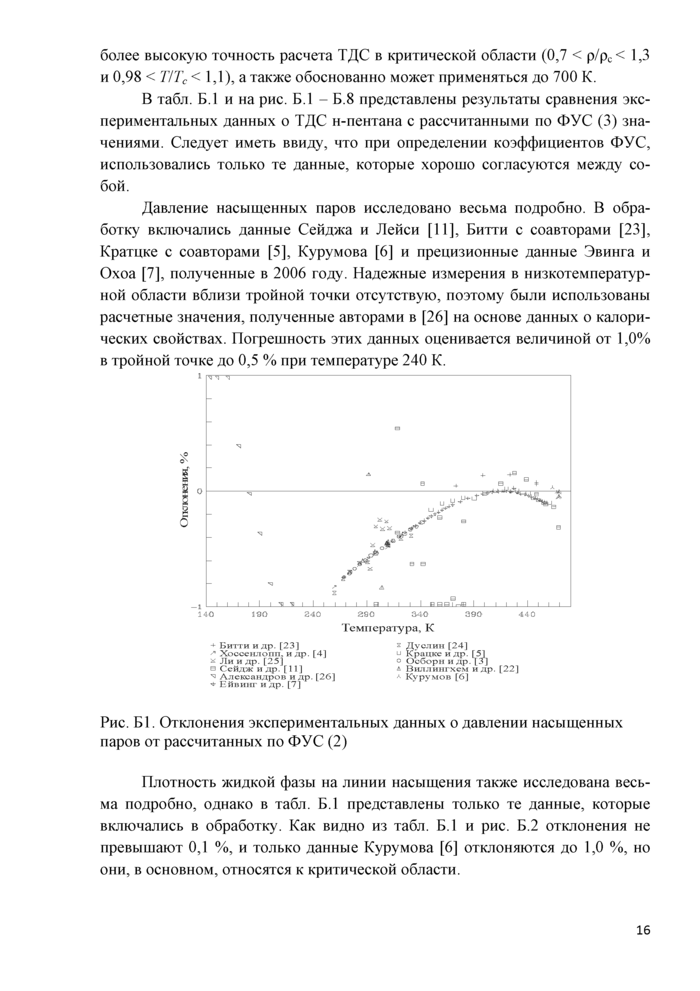
Давление насыщенных паров исследовано весьма подробно. В обработку включались данные Сейджа и Лейси [II], Битти с соавторами [23], Кратцке с соавторами [5], Курумова [6] и прецизионные данные Эвинга и Охоа [7], полученные в 2006 году. Надежные измерения в низкотемпературной области вблизи тройной точки отсутствую, поэтому были использованы расчетные значения, полученные авторами в [26] на основе данных о калорических свойствах. Погрешность этих данных оценивается величиной от 1,0% в тройной точке до 0,5 % при температуре 240 К.
|
|
140 ISO 240 280 540 590 440
Температура, К
- Битти и др. (23)
• Хосеснлопп, и ло. [41 Ли и др. [25)
° Сейдж и др [ 111
Александров и др [26] ■» I'itninii идр. [7]
• Дуслин [24]
Крацкс идр. Г51
о Осборн идр. [У]
• Внллингхсч и др. [22]
• Курумои [6] |
Рис. Б1. Отклонения экспериментальных данных о давлении насыщенных паров от рассчитанных по ФУС (2)
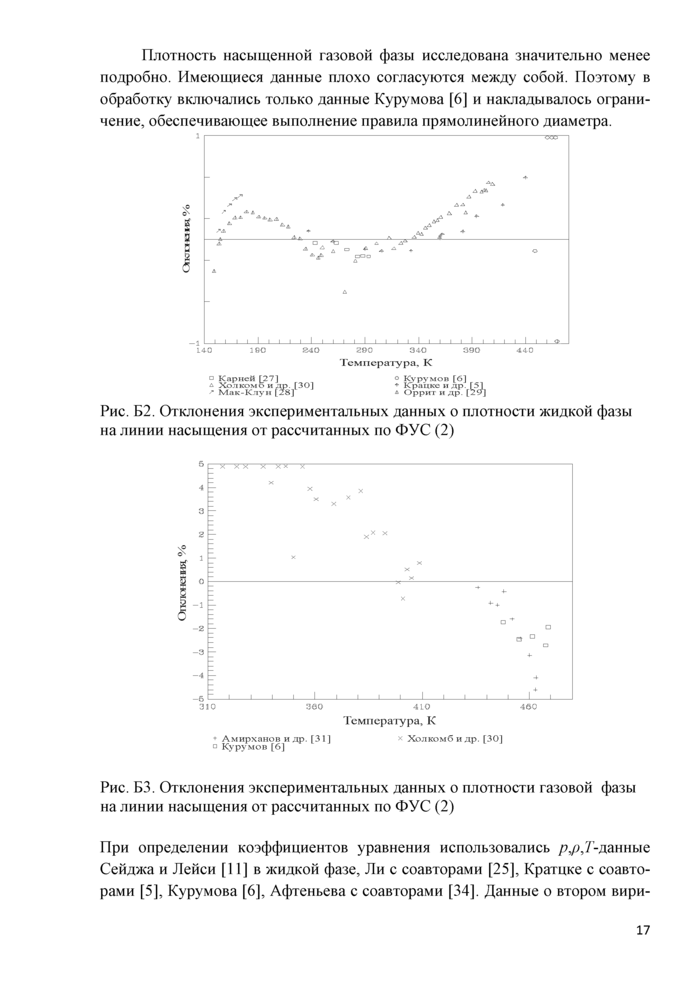
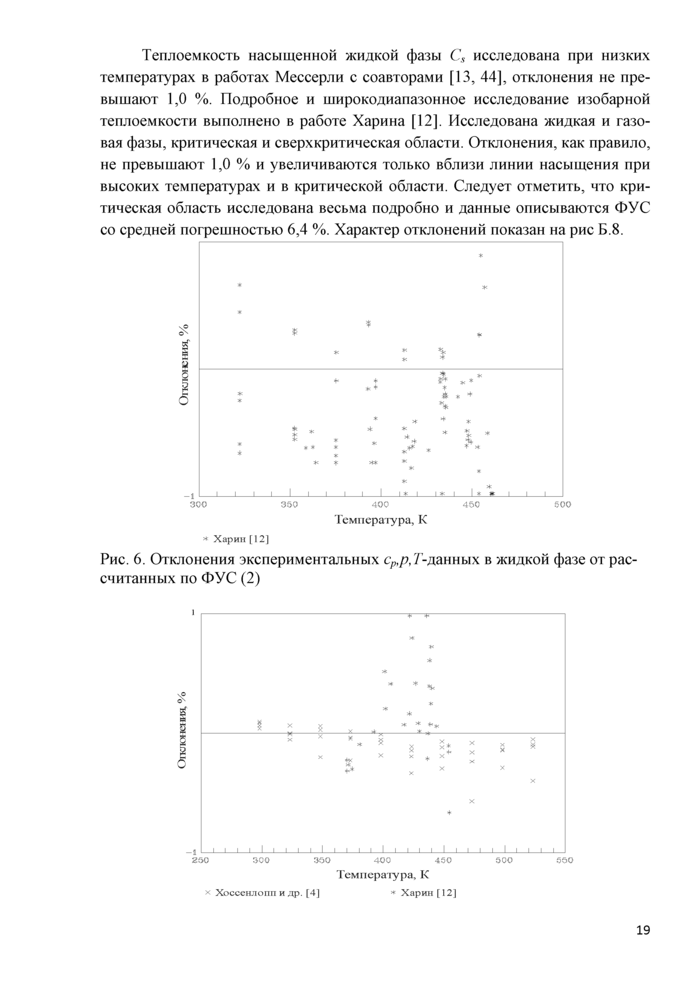
Плотность жидкой фазы на линии насыщения также исследована весьма подробно, однако в табл. Б.1 представлены только те данные, которые включались в обработку. Как видно из табл. Б.1 и рис. Б.2 отклонения не превышают 0,1 %, и только данные Курумова [6] отклоняются до 1,0 %, но они, в основном, относятся к критической области.
16
УДК 547.216:536.7
ГОСУДАРСТВЕННАЯ СЛУЖБА СТАНДАРТНЫХ СПРАВЧНЫХ ДАННЫХ
Таблицы стандартных справочных данных
н-Пентан. Термодинамические свойства
в диапазоне температуры от тройной точки ГСССД
до 700 К при давлениях до 100 МПа 291-2013
Tables of Standard Reference Data
n- Pentane. Thermodynamic properties
in the range from the triple point temperature GSSSD
up to 700 К at pressures up to 100 MPa 291-2013
3
ДЕПОНИРОВАННАЯ РУКОПИСЬ
УДК 547.216:536.7
Таблицы стандартных справочных данных ГСССД 291 - 2013. н-Пептан. Термодинамические свойства в диапазоне температуры от тройной точки до 700 К при давлениях до 100 МПа /Григорьев Б.А., Герасимов А. .А., Александрова И. С.. Российский научно-исследовательский центр информации по стандартизации, метрологии и оценке соответствия ФГУП «СТАНДАРТИНФОРМ» - М., 2013, - 54 с.: - Ил. - Библиогр. назв. - Рус. - назв. Депонированы во ФГУП «СТАНДАРТИНФОРМ» 31.10.2013 г., № 883- 2013 кк.
Таблицы стандартных справочных данных о термодинамических свойствах н-Пентана рассчитаны по фундаментальному уравнения состояния ФУС, описывающему свободную энергию Гельмгольца.
Авторы: Григорьев Б. А
Герасимов А. А.
И. С. Александров
4
Таблицы стандартных справочных данных о термодинамических свойствах н-пентана рассчитаны по фундаментальному уравнения состояния ФУС, описывающему свободную энергию Гельмгольца «(р.Г> в зависимости от температуры Т и плотности р. Свободная энергия Гельмгольца а(р, Т) представлена в виде суммы идеально-газовой части a°(Sj) и избыточной части и(д,т).
В свою очередь избыточная часть свободной энергии Гельмгольца представлена в виде разложения в ряд по степеням приведенной температуры г и приведенной плотности г)' с полиномиальными а?о\, экспоненциальными аЕхр и гауссовыми aGBS членами для лучшего описания свойств в критической области.
ar(jyS) — arFc, +ar^ +arGBS = exp(-r)+
+ Z exP(-/71 )’ -p, (r-r, У)
где S = plpc; г = TJT\ pc, Tc - параметры приведения, в качестве которых приняты критические значения. В частности для н-пентана: рс= 3,2155 кг/кмоль, Тс= 469,60 К.
Определение коэффициентов ФУС и оптимизация формы уравнения производились по алгоритму, реализующему метод случайного поиска с возвратом при неудачном шаге [1].
Минимизируемый функционал содержал как слагаемые, ответственные за точность аппроксимации результатов измерений разнородных данных о термодинамических свойствах, так и различные ограничения, накладываемые в виде неравенств на термодинамическую поверхность. Основными видами ограничений являлись: критические условия, правило Максвелла, контроль кривизны идеальных кривых, положительность теплоемкости, правило прямолинейного диаметра, контролирование знаков производных различных термодинамических величин и т.д. Эти ограничения обеспечивают «физическую» форму поверхности состояния и улучшают экстраполяционные возможности уравнения.
„ fcgr s0° , , <5г, г /‘t-р.. ir‘bp
- ЙГ 7Г 1 + ‘"Zoi- * L^dl + Rk^dT-
Безразмерная идеально-газовая часть свободной энергии Гельмгольца определяется по соотношению
где So = Ро/рс; т* = TJTq, ТоуРо - вспомогательная опорная точка (7’0= 298,15 К; /?0 = 101325 Па); р0- плотность идеального газа при температуре То и дав-
5
лении /?0; *e, si - соответственно энтальпия и энтропия в идеально-газовом состоянии при температуре 7о.
Для расчета функции необходимы данные об изобарной теплоемкости в состоянии идеального газа . Выли приняты значения, полученные в Термодинамическом Исследовательском Центре [2] и аппроксимированы уравнением
c4=i^ о)
1--J
где R = 8,314472 Дж/(мольК) - универсальная газовая постоянная. Значения коэффициентов ct представлены в табл. 1.
Термодинамическое соотношение (3) совместно с эмпирической зависимостью (4) приводят к следующей формуле для расчета и*
■г
а9 = X ai г* + огз 1"г + <**г1** + in£ (5^
/=-з
Значения коэффициентов а\ представлены в табл. 1.
Таблица I. Значения коэффициентов уравнений (4) и (5) для идеально-газовых функций н-пентана
|
/ |
ct |
|
|
-3 |
|
-0,2515444 |
|
-2 |
-0,3192613106 |
3,570695 |
|
-1 |
0,5725909-104 |
-29,89561 |
|
0 |
-0,3124129-102 |
-38,70635 |
|
1 |
0,1273237 |
41,75795 |
|
2 |
-0,9715112-1 O'* |
0,7238691 |
|
3 |
0,2914819-10'7 |
-32,24129 |
|
4 |
- |
-12,19316 |
Коэффициенты ФУС в форме (2) определялись по отобранным авторами разнородным экспериментальным данным о термодинамических свойствах н-пентана: давление насыщенных паров рх. [3-7], плотность жидкой pi [5, 8-10] и газовой фазы pv [6] на линии насыщения, второй В и третий С вири-апьные коэффициенты [6], p9v9T-данные [5,6,11], срр9Т- и с\.,у,7'-данные [12-14], скорость распространения звука w [10,14,15]. Оптимизированная форма уравнения (2) имеет вид (6). Коэффициенты уравнения и степени при температуре и плотности представлены в таблице 2. Более подробно процедура построения ФУС описана в Приложении.
6
|
<*r(T,S)=arPol+arExp+aGBS |
exp^^1’')+
i=7 |
+ 2>/^ exp(-//.)2 -pt (r-r, )2)
/=12
|
Таблица 2. Значения коэффициентов и показателей степени ФУС (6) |
|
к |
Пк |
1к |
dk |
_&_ |
|
1 |
0.03843469943171 |
1.353 |
4 |
|
|
2 |
1 416685474406 |
0.219 |
1 |
- |
|
3 |
-0.8321311024950 |
0 394 |
1 |
- |
|
4 |
0.4498740983986 |
1.94 |
2 |
- |
|
5 |
-1.473541352142 |
1.463 |
2 |
- |
|
6 |
0 1449480544422 |
0.502 |
3 |
- |
|
7 |
-1.001425083284 |
1.172 |
1 |
1 |
|
8 |
-1.463383940533 |
2409 |
1 |
2 |
|
9 |
-1.063698400458 |
3.027 |
3 |
2 |
|
10 |
-0.4965197180555 |
4092 |
2 |
2 |
|
11 |
-0 0008571960893994 |
2 519 |
8 |
1 |
|
12 |
0 7939001246115 |
2.627 |
1 |
- |
|
13 |
0 2564831077932 |
2624 |
1 |
- |
|
14 |
-0.02116009691532 |
3.173 |
2 |
- |
|
15 |
-0.3201840734624 |
2 541 |
3 |
- |
|
16 |
0 007046991758369 |
4 101 |
3 |
- |
|
17 |
0.01771175595068 |
0 798 |
2 |
- |
|
|
Окончание табл. 2 |
|
к |
Пк |
Ук |
Ук |
|
|
12 |
-1.066 |
-1.178 |
1.214 |
0.784 |
|
13 |
-0.673 |
0 172 |
1.59 |
0.795 |
|
14 |
-1.325 |
0.04 |
0.941 |
1.932 |
|
15 |
-1.121 |
-0 464 |
0.547 |
0.685 |
|
16 |
-1.721 |
-0 198 |
0.1 |
2.059 |
|
17 |
-1.478 |
-0 115 |
1.815 |
1.271 |
|
Термодинамические свойства рассчитывались по ФУС (6) с использованием известных дифференциальных соотношений термодинамики:
ПЛОТНОСТЬ
(7)
(8)
(9)
(10)
изобарная теплоемкость
7F <a"+“")+ i + 2&;+tfy„ •
(ID
(12)
где нижний индекс при а показывает частную производную по соответствующей переменной.
Конкретные аналитические зависимости различных производных термодинамического потенциала, входящие в уравнения (7) -(12) представлены, в Приложении, а также, например, в [ 16].
За термодинамическое начало отсчета при составлении таблиц термодинамических свойств н-пентана принято состояние равновесного молекулярного кристалла при температуре 0 К. Значения энтальпии /?0 и энтропии л0 во вспомогательной точке отсчета на линии насыщения жидкой фазы определены поданным [13] ( Но = 541,75 кДж-кг*|,50 = 3,6516 кДжкт'-К ‘).
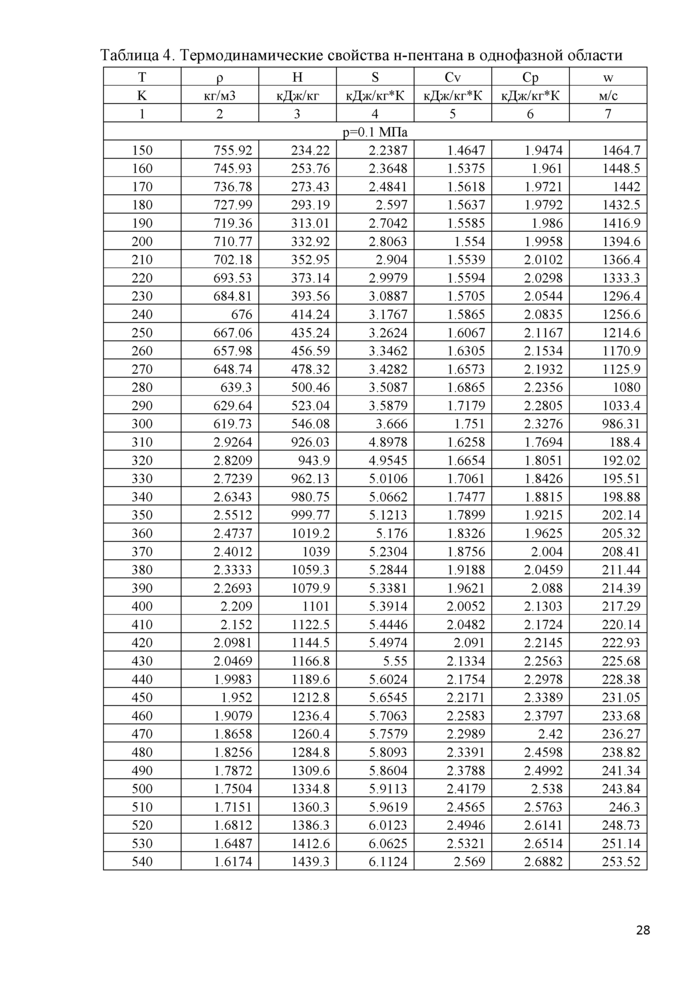
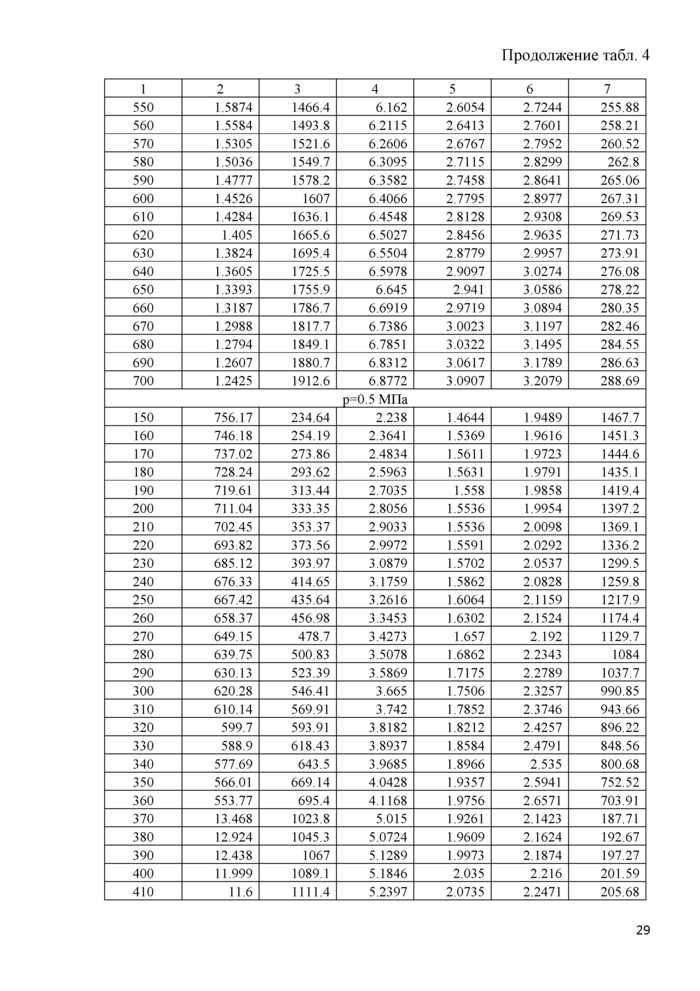
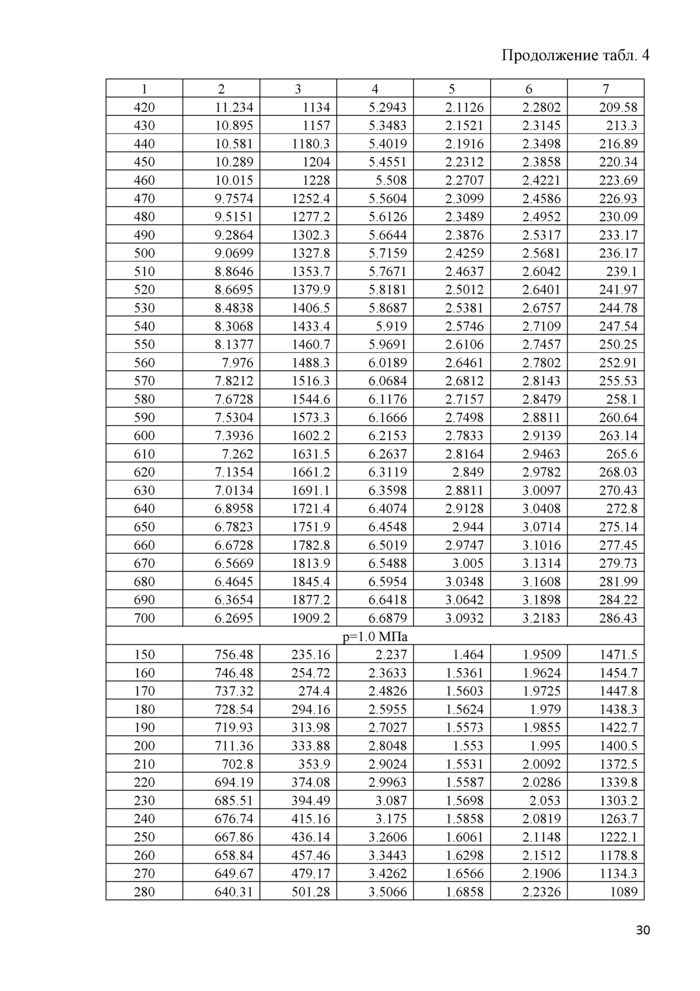
Таблицы термодинамических свойств н-пентана рассчитаны по ФУС (6) в диапазоне температуры от тройной точки (7", = 143,47 К) до 700 К при давлениях до 100 МПа. Свойства в однофазной области представлены в табл. 4, свойства на линии насыщения - в табл. 5. Линия плавления описана эмпирическим уравнением Симона - Глатцеля
(13)
где/?* = 660,7 МПа; с = 1,67. Значения коэффициентов уравнения (13) приняты по данным работы [17] и они носят оценочный характер.
Величина неопределенности расчетных значений термодинамических свойств оценена в результате сравнения с наиболее надежными экспериментальными данными и уравнениями. Представленные ниже в табл. 3 оценки даны для жидкой фазы Ф (Т < Тс, р > 1,3/?<•), для газовой фазы Г(Т< Тс> р < 0,7/?с), для сверхкритического флюида Ф (Т > 7*с, исключая критическую область) и для критической области К(ТЯ<Т< 1,05/с, 0,7рс< р< 1,3рс)
|
Таблица 3. Оценки неопределенности расчетных значений термодинамических свойств |
|
Свойство |
Неопределенность, % в области |
|
Ж |
Г |
Ф |
К |
|
А |
- |
0,1 -0,15 |
- |
0,7 |
|
Pi |
0,1 -0,15 |
|
- |
до 1,3 |
|
Ру |
- |
Ъ»
1
ю
о |
- |
до 3,0 |
|
Р-Р-Т |
0,15-0,25 |
0
1
о
00 |
0
СЛ
1
р
'•si |
2,0 - 3,0 |
|
Ор |
1,0- 1,5 |
1,2-2,0 |
1,0- 1,5 |
0
1
о
о |
|
с\. |
ю
0
1
'VI
о |
2,0-4,0 |
1,0- 1,5 |
8,0- 12,0 |
|
W |
1,0- 1,5 |
- |
- |
- |
|
|
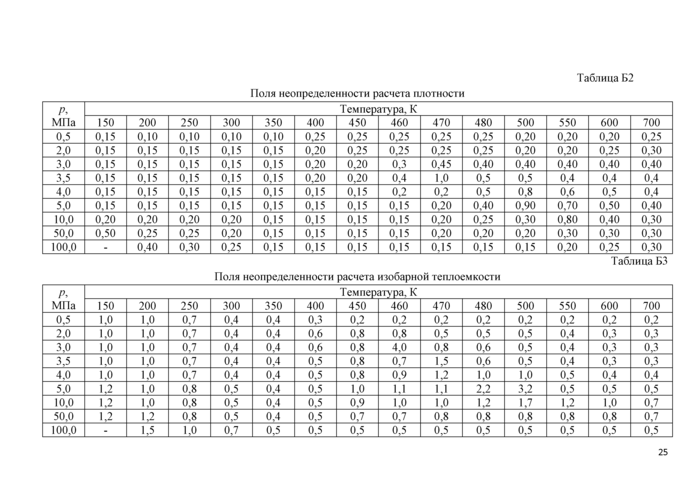
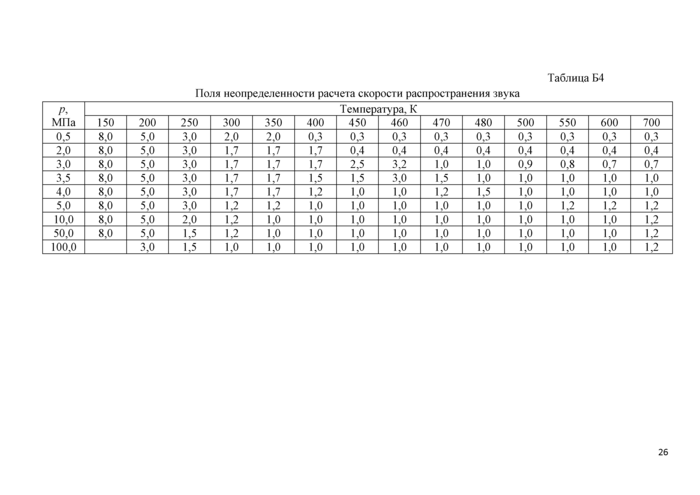
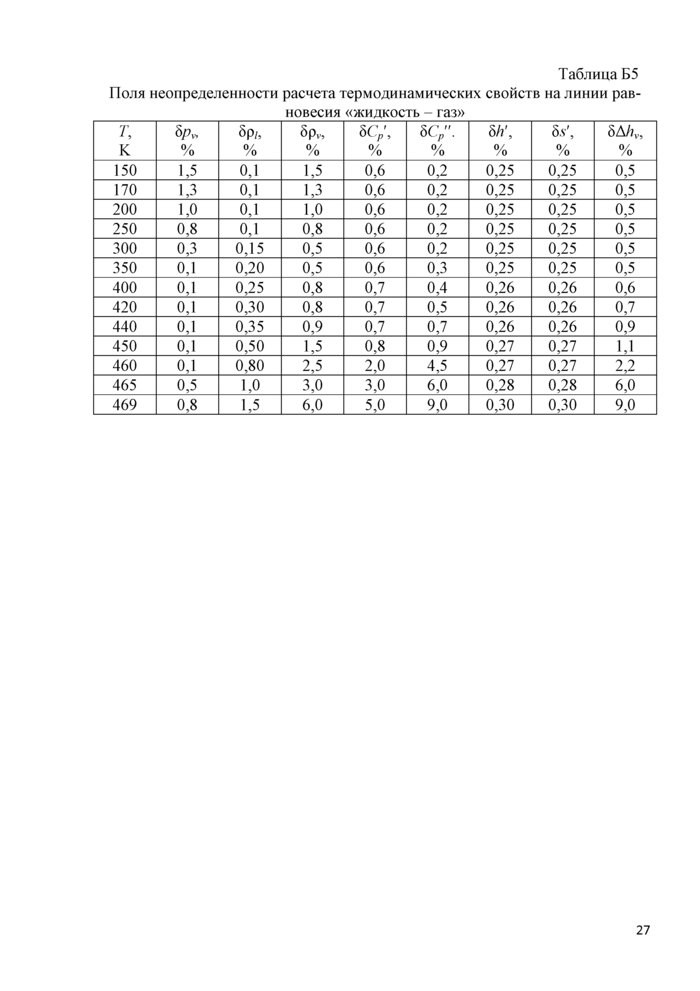
Более подробные сведения о результатах сравнения расчетных данных со всеми имеющимися экспериментальными данными и поля неопределенностей представлены в Приложении Б. |
9
ПРИЛОЖЕНИЕ А
Методика разработки уравнения состояния.
При разработке ФУС (2) использовались разнородные экспериментальные данные о термодинамических свойствах н-гептана - p,v,'/’-данные, данные о втором В и третьем С вириальных коэффициентах, упругость насыщенных паров pv, плотность насыщенной жидкой pi и газовой фазы pv, теплоемкость насыщенной конденсированной фазы с„ изохорная cv и изобарная ср теплоемкости, энтальпия И, скорость распространения звука w.
В минимизируемый функционал включалось несколько слагаемых, каждое из которых ответственно за определенную категорию обрабатываемых термодинамических величин:
где я, - коэффициенты ФУС, арл- слагаемые ФУС, определяемые по (14), — -
<т;
вес опытной точки, ао - экспериментальное значение термодинамического свойства.
В данном случае функциональная связь задавалась уравнением
apj = exp(-y,Sp ), (A2)
а коэффициенты я определялись посредством оптимизационного алгоритма, описанного ниже. Для расшифровки правой части формулы (А1) использовались известные дифференциальные соотношения термодинамики (6) -(11). Кроме включения в обработку' экспериментальных данных о различных термодинамических свойствах н-пентана, также применялась система ограничений, накладываемых в виде неравенств на термодинамическую поверхность. Основными видами ограничений являлись: критические условия, правило Максвелла, контроль кривизны идеальных кривых, положительность теплоемкостей, правило прямолинейного диаметра, контролирование знаков производных различных термодинамических величин и т.д. Эти ограничения обеспечивают «физическую» форму поверхности состояния и улучшают экстраполяционные возможности уравнения.
При разработке ФУС (2) для н-пентана была применена модификация метода случайного поиска с возвратом при неудачном шаге. Алгоритм модифицирован введением элементов детерминированного поиска на шаге корректировки величины шага поиска и выбора направления.
10
1