ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

ТЕОДОЛИТЫ. МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ ДИАМЕТРОВ

ГОРИЗОНТАЛЬНОГО КРУГА

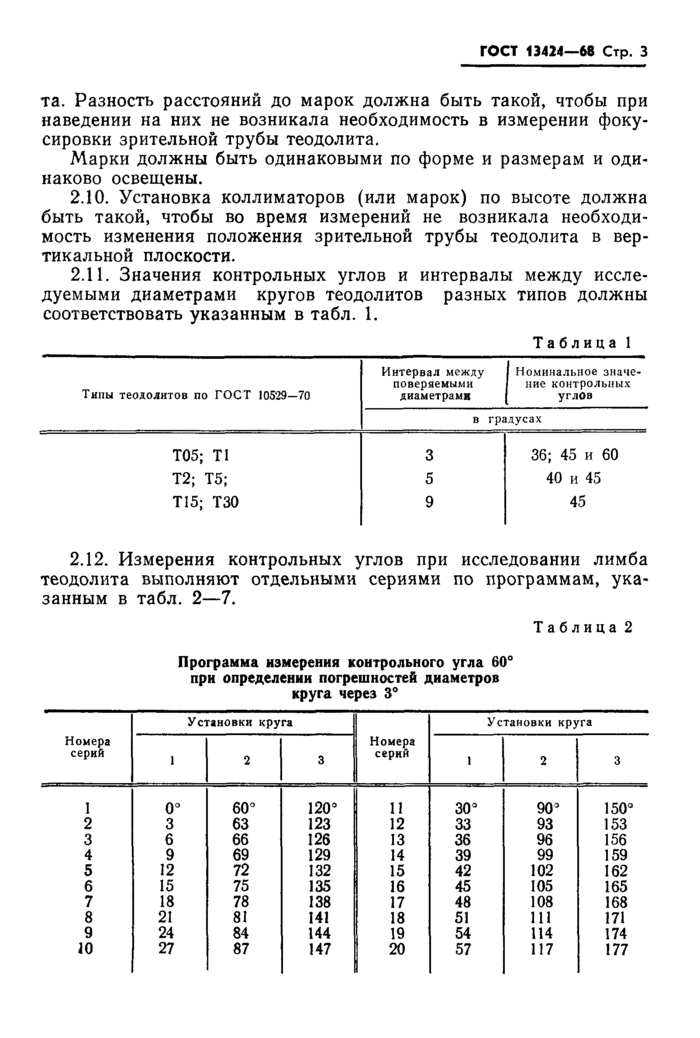
ГОСТ 13424-68

Издание официальное

государственный комитет стандартов

СОВЕТА МИНИСТРОВ СССР

Москва

УДК 528.5.001.4(083.74)    Группа    П49

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

ТЕОДОЛИТЫ. МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ ДИАМЕТРОВ ГОРИЗОНТАЛЬНОГО КРУГА

Teodolites. Methods for determination of errors of horizontal circle diameter

Утвержден Комитетом стандартов, мер и измерительных приборов при Совете Министров СССР 2 января 1968 г. Срок введения установлен

с 01.07. 1968 г.

Несоблюдение стандарта преследуется по закону

Настоящий стандарт устанавливает методы определения полных погрешностей диаметров горизонтальных кругов (лимбов) теодолитов.

Стандарт не устанавливает методов определения короткопериодических погрешностей штрихов лимбов, а также методов пред-приятий-изготовителей, выполняемых до установки круга в прибор.

1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ

1.1.    Погрешность диаметра лимба — отклонение фактического положения диаметра лимба, образованного парой взаимно противоположных штрихов, от его расчетного положения в угловых единицах.

Сумма погрешностей диаметров, равномерно расположенных по кругу через интервал Дф, равна

180°—Д tp 0

где ф=0, Дф, 2Дф, . . . , 180°—Дф.

Погрешность начального (нулевого) диаметра не равна нулю.

1.2.    Полная погрешность диаметра х<р состоит из систематической (л;* ) и случайной (х_п ) погрешностей.

Издание официальное    Перепечатка    воспрещена

Переиздание. Январь 1977 г.

©Издательство стандартов, 1977

Стр. 10 ГОСТ 13424-68

Число нормальных уравнений (4) будет равно числу исследуемых диаметров круга (л).

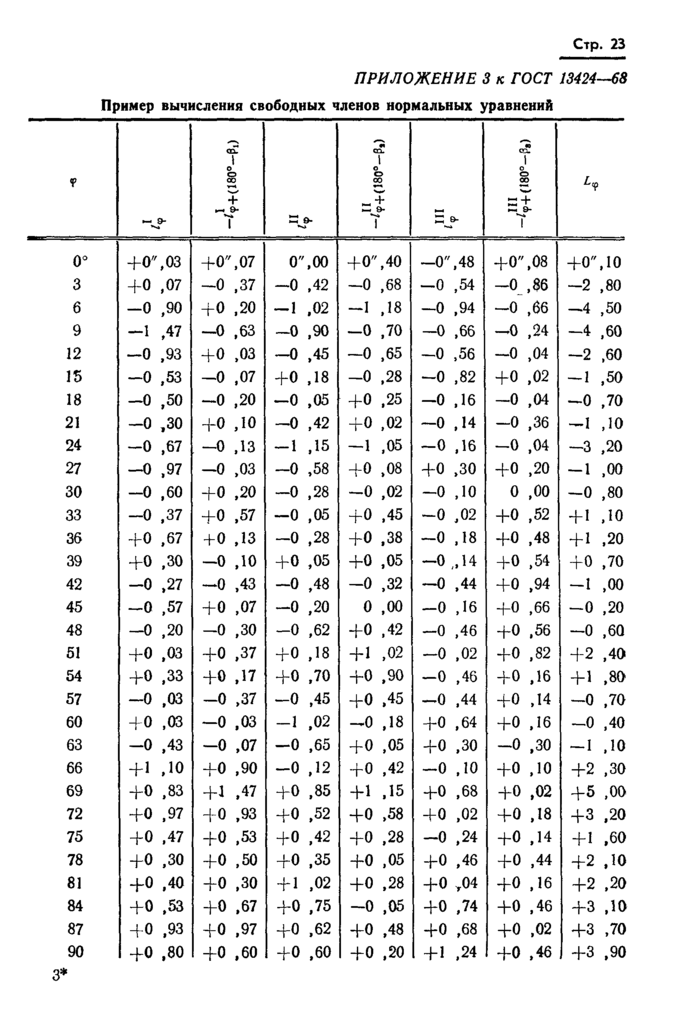
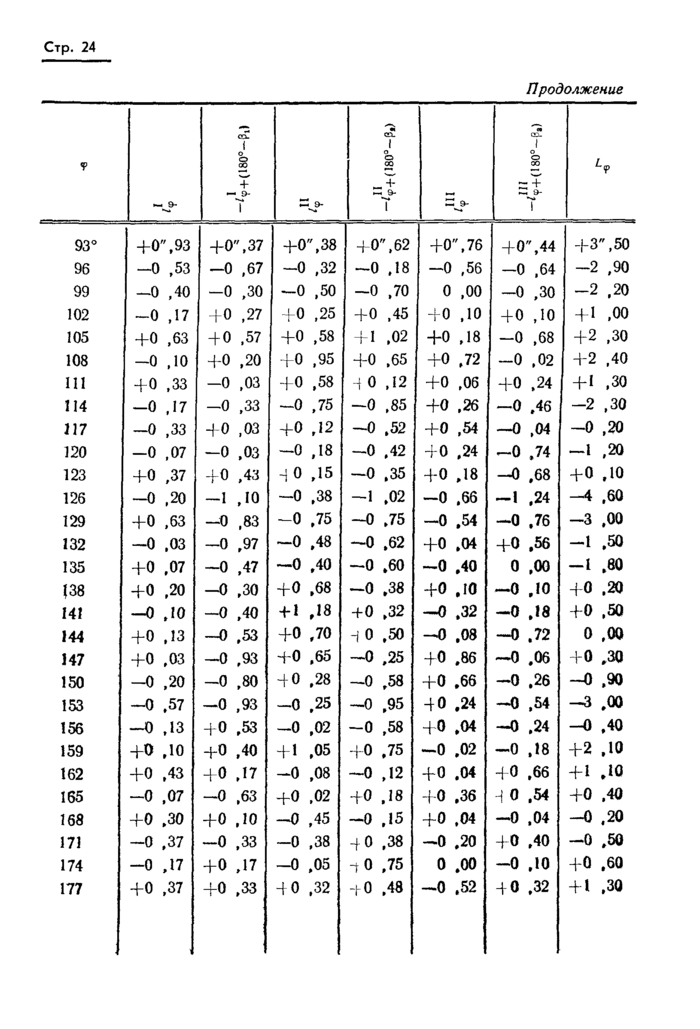
Пример вычисления свободных членов нормальных уравнений приведен в приложении 3.

3.2.2.    Коэффициенты нормальных уравнений (4) образуют вырожденную квадратную матрицу.

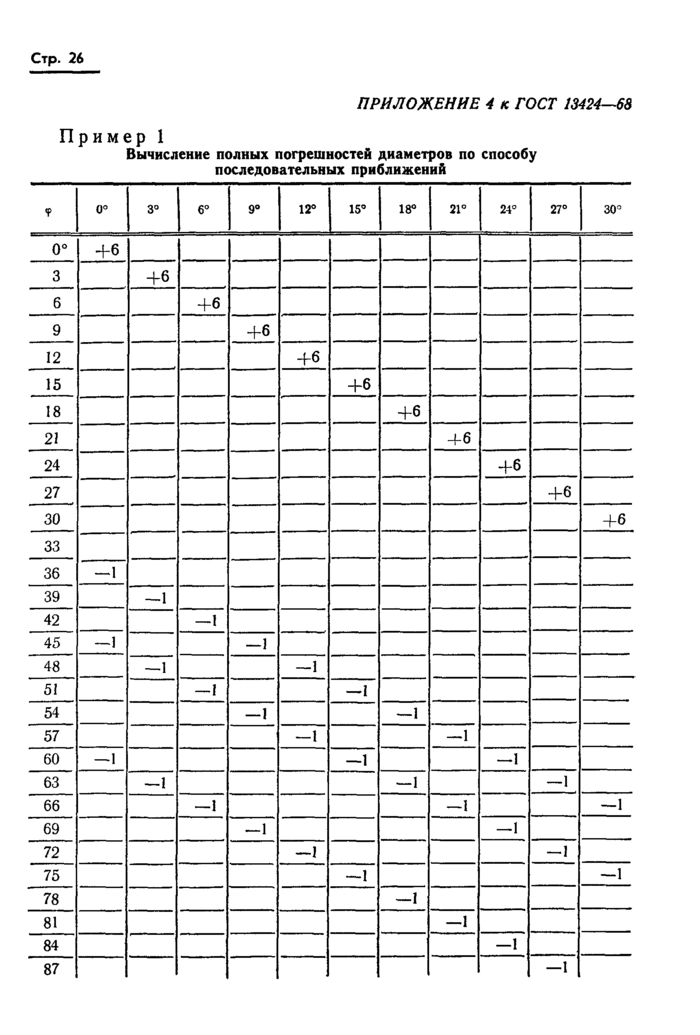
Если прямая матрица А_п, п не подвергается преобразованию, то система нормальных уравнений (4) решается способом последовательных приближений.

За значения неизвестных в первом приближении пр-инимают среднее арифметическое из ошибок диаметров, вычисленных по формулам 10, 11, 13 или 11, 12.

Примеры вычисления полных погрешностей диаметров по I способу приведены в приложении 4.

3.2.3.    При вычислении погрешностей по II способу вырожденную матрицу преобразуют в совместную и определенную, а вычисления производят с помощью заранее вычисленных коэффициентов обратной матрицы (весовые коэффициенты).

Обратная матрица А7\ 60-го порядка (для р = 36; 45 и 60°) приведена в приложении 5.

Обратная матрица Ап\ 36-го порядка (для р = 40 и 45°) приведена в приложении 6.

3.2.4.    Полные погрешности диаметров вычисляют путем умножения коэффициентов обратной матрицы на свободные члены нормальных уравнений (4). Для этого коэффициент обратной матрицы, записанный в первом столбе, умножают на свободный член 1-го нормального уравнения; записанный во втором столбе — на свободный член 2-го нормального уравнения; записанный в третьем столбе—на свободный член 3-го нормального уравнения и т. д.

Для определения погрешности какого-либо одного диаметра необходимо получить сумму произведений всех коэффициентов обратной матрицы, записанных в одной строке, на свободные члены всех нормальных уравнений.

Контролем правильности вычисления по II способу служит равенство нулю суммы всех вычисленных погрешностей диаметров

п

=0, где п — число исследуемых диаметров круга.

3.2.5. При вычислении по I и II способам вычисляют среднюю квадратическую погрешность единицы массы (направления, измеренного четырьмя полуприемами), ц и среднюю квадратическую-погрешность т_Х(р определения полной погрешности диаметра

ГОСТ 13424—М Стр. 11

3.2.6.    Среднюю квадратическую погрешность единицы массы (jx) находят по формуле

• «

где 6 — случайные погрешности измерения контрольных углов, вычисляемые из уравнений (3) путем подстановки в них найденных значений полных погрешностей диаметров N — число всех уравнений погрешности (3), равное числу измеренных углов Л_?; п — общее число независимых установок круга, равное числу исследуемых диаметров или числу нормальных уравнений;

S — число серий, в которых измерены контрольные углы А_г.

3.2.7.    Среднюю квадратическую погрешность определения полной погрешности диаметра (тх?) вычисляют по формуле

= Qu>    (⁷>

где Qa — обратная масса полной погрешности диаметра, равная квадратичному коэффициенту обратной матрицы.

Примечание. При исследовании круга через 3° и использовании трех углов {5, равных 60; 45 и 36°, Q = 0,20.

При исследовании круга через 5° и использовании двух углов (3, равных 40 и 45°, Q=0,37.

3.3. При вычислении полных погрешностей по III способу (способу Елисеева) применяют следующие формулы

₆ -2^-/£_+в0. .

-’

а -2£-£^«.+4+135° . _ю---------

10    — 2^5>°—^+зб°+4+108*+ 2/₉+М4° .

•*“-¹—б--*

ft ,п 0)®+(0⁶ _Мо+С0® ₇,о+0)«₊₁₀8^+“®+ 144° .

«)<Р    =- —- *

ГОСТ 13414-6» Стр. 13

l_f и /_¥+бо» — уклонение углов A_v измеренных на установках круга ф и ф₊бо° от среднего арифметического С,- (/=ф=0; 3; б;

.....57°) в каждой отдельной серии;

б) при контрольном угле 02 = 45°

~    **'?+45‘^> —    Х_т\

•^?+90^o==-^ip+90^o •Х'т' •^<р+135⁰—^:^<р+13б° ^т\    (11)

_где    “    __    ■*Н-45°+-У|-90°    +*,>+135°

^<р 1 JCy -f 90° -К<р+45°    4-    45°

^С<р+Х35° =-*<р+90^о +Ар+90°;

⁼⁼Су Af J ltp+ 45° — Cj—Aif4- 45°;

/<р+90° =Cj—Л_?+ 90°;

/' = Ф = 0; 3; 6; . , . ; 42° при исследовании круга через 3°; /=<р=0; 5; 10;    ; 35° при исследовании круга через 5°;

/=Ф=0; 9; 18; ... ; 36° при исследовании круга через 9°;

в) при контрольном угле 04=40°

JCm — ^Xnv> -*9+40°'““-*9+40^о хтл IV —    — IV    “    ~

•*9+80°---*<р + 80°    "^/я*    -*9+12Э^4>===-^9+120°    ^jTZ >

-*^+160^о=:г**9+Ш^о —^р^ЮО°“-*Ф+200° fmi -*9+240°⁼-*9+240° —-*m] -*9+280^o=-*9+280°

x\ 4-320° =-*9 +320° —-*_m,    (12)

-     *у-Н0^о+*(р-Ь    БО^^УЧ-^Э⁰    +*<p+16QQ    +*y+2TO^&~^^X9+240^o +

9

+^x<p+ 280^о+^у+320°

9    ’

Ху+№=1у * -*9+80° =-*9+40° +^+.40°;

•*9+120° ⁼-*ф+ 80°Ч“^ф+ 80°) -*9 + 160^о==-^9+,120°”^'^?+Л^⁰*

-*9+200° =-*9+ 160°+^<p+ *60°; -*9+L240° = **9 + 200° +Ар + ²⁰⁰°5 •*9+280° =-*9+ 240°+ ^9+240°^ -*9 + 320° = -*9+:280° +^9 + ²⁸°⁰»

l₉=Cj— А₉; /9₊40°=£/~^9+40°; /<р+80^в=С/—Л?+80°;

Д+120°—¹Су—Лф +120°; /9+160° ^ssc^/ ^9+160° ; ^9+ гоо⁰³^^ -Ау+200°,

/9+240° = ^—Аф+240°; /9+280° — ^—Л_?+280°;

у=0; 5; 10; . . . ;35°;

Стр. 14 ГОСТ 13424-68

г) при контрольном угле р₃=*36°

JH_    "    .    „III    -    -

— ^Лт> ^д'*р+36°=^:г^<р+36°—^хт\

^Х9+ 72«Л:9₊ 72°”Х_т; _Х'Уиг=Х₉+ 108 III    -

^9 + 144° — Х₉₊ 144°—^;

где

_    *9+    36°+*^Г9+    72°+-*<р-Н08°+-*9+144^в    .

^лт--'    I----1

о

•^9+ 36°“£р > *^9+ 72°—Х9+ 36°Н“ ^9+ 36°;

-^9+ 108^o=*^9+ 72°+ /9+ 72*; -£9 + 144°=-*;9+ 108° + ^+

I9 ⁼ Cj А₉;    j—А₉ +зб°;

/9+ 72°==Су—А(р₊ 72°; 1₉₊ Ш8° —Cj—A_f+ 108°;

/-V^е0; 3; 6;    ;    33°.

3.4.1.    При исследовании круга через 3° при помощи трех контрольных углов 36; 45 и 60° вычисления погрешностей диаметров осуществляют в следующем порядке:

а)    по формулам (10) вычисляют погрешности диаметров х\ из обработки результатов измерений контрольного угла 60°;

б)    по формулам (11) вычисляют погрешности диаметров из обработки результатов измерений контрольного угла 45°;

в)    по формулам (13) вычисляют погрешности диаметров х\^и из обработки результатов измерений контрольного угла 36°;

г)    по формуле

л» — Е(л4+л:”+jc"¹)    (14)

з

находят окончательные значения погрешностей диаметров;

д)    по формуле

^т«~]/ -тг    <¹⁵>

вычисляют среднюю квадратическую погрешность полной погрешности диаметров круга,

где    Ьх\-=х₉ —х\, Aje"=j:_f —л",    —jc"¹.

3.4.2.    Пример вычисления полных погрешностей диаметров круга по формулам (10), (II) и (13) и оценка точности по формуле (15) приведены в приложении 8.

Стр. 16 ГОСТ 13424-68

bj = -~[^icos2y<pj"_=o ,    (20)

где х₉ — полные погрешности диаметров;

i — порядковый номер полной погрешности диаметра (i=l;

2; 3);

/ — порядковый номер коэффициента ряда Фурье, (/=2, 4,

6, 8.......к);

п — число полных погрешностей диаметров.

4.3.    При вычислении систематических погрешностей ограничиваются вычислением коэффициентов ряда Фурье, определяющих первые четыре гармоники.

4.4.    Примеры вычисления систематических погрешностей диаметров приведены в приложении 9.

4.5.    Случайные погрешности диаметров круга вычисляют как разность между полными и систематическими погрешностями:

=Х₉ — Ха .    (21)

4.6.    Случайные погрешности диаметров круга могут быть определены графически по вычисленным значениям полных и систематических погрешностей. Для этого строят график погрешностей x_f и х_а и случайные погрешности определяют как разность одноименных ординат (см. приложение 10).

5. ОФОРМЛЕНИЕ РЕЗУЛЬТАТОВ ПОВЕРКИ

5.1.    На горизонтальные круги теодолитов, признанные годными при поверке органами Государственного комитета стандартов Совета Министров СССР дается свидетельство установленной формы.

5.2.    Результаты периодической ведомственной поверки вносят в соответствующий документ, составленный органами ведомственного надзора и согласованный с органами Государственного комитета стандартов Совета Министров СССР.

5.3.    Результаты поверки горизонтальных кругов теодолитов техническим контролем предприятия-изготовителя оформляют путем выдачи выпускного аттестата.

5.4.    Горизонтальные круги теодолитов, не удовлетворяющие требованиям ГОСТ 10529-70 и настоящего стандарта, к выпуску и применению не допускаются.

Замена

ГОСТ 10529-70 введен взамен ГОСТ 10529-63.

Стр. 17

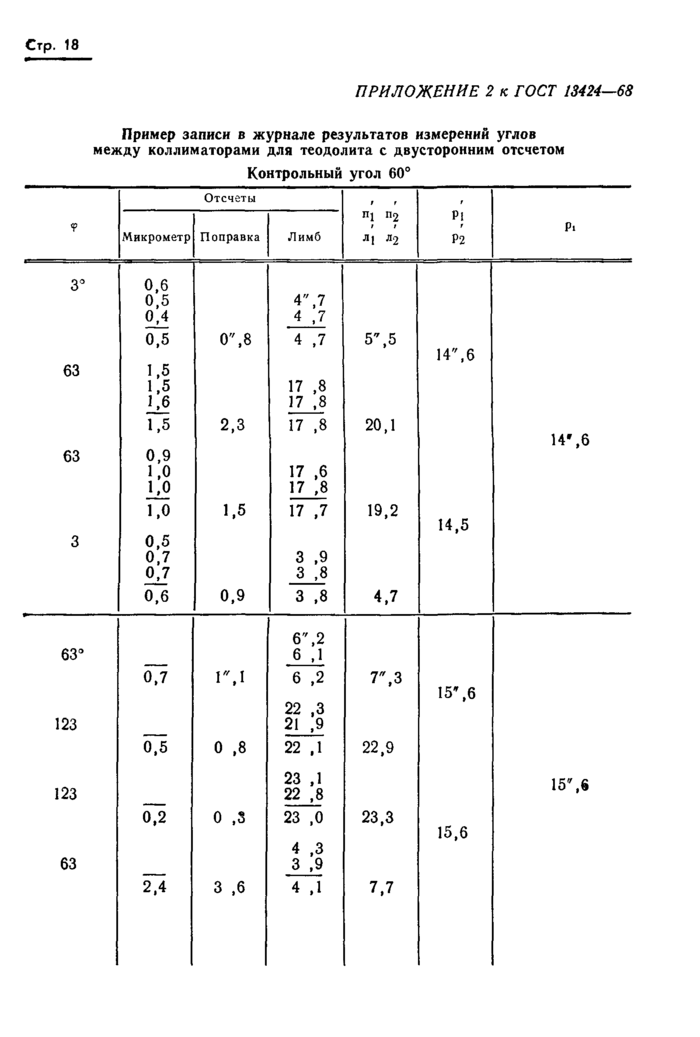
ПРИЛОЖЕНИЕ 1 к ГОСТ 13424-68

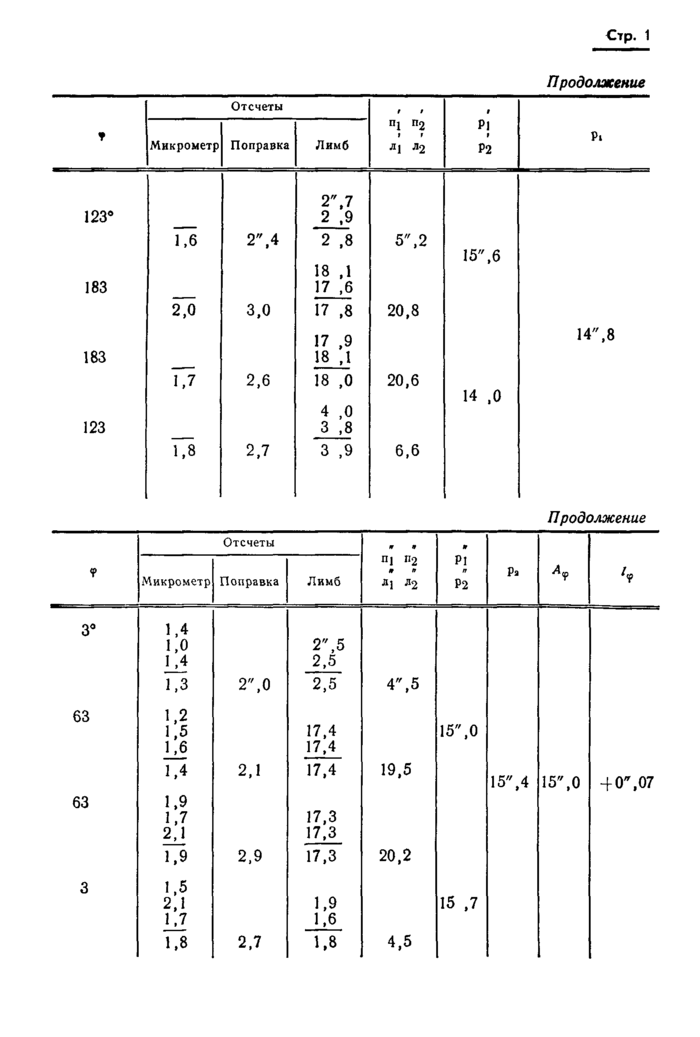
Пример записи в журнале результатов измерений углов между коллиматорами для теодолита с односторонним отсчетом

Op. 1

Стр. 2 ГОСТ 13424-68

1.3.    Систематической погрешностью называют ту часть полной погрешности, которая представляется периодическим рядом и вычисляется с заранее ограниченным количеством членов этого ряда (см. п. 4.3).

1.4.    За случайную погрешность принимают разность между полной и систематической погрешностью диаметров

Х_п =Х:р —Ха .

2. АППАРАТУРА И ПОРЯДОК ПРОВЕДЕНИЯ ИЗМЕРЕНИЯ

2.1.    Определение погрешностей диаметров горизонтального круга теодолитов должно производиться методом калибровки, основанным на последовательном откладывании на исследуемом круге значения одного или нескольких контрольных углов, принимаемых за постоянные.

2.2.    При измерении одного контрольного угла температура воздуха не должна изменяться более чем на 3°С.

2.3.    Контрольные углы могут быть образованы направлениями на два коллиматора или две марки, или двумя гранями образцового многогранника, если исследуют лимб, вмонтированный в теодолит, или двумя парами микроскопов, если отделенный от прибора лимб компарируется на специальном приборе для исследования круговых шкал.

2.4.    Номинальное значение |3 контрольного угла должно укладываться в окружности или полуокружности целое число раз.

Разность между действительным значением А₉ контрольного угла и его номинальным значением р должна быть меньше половины цены деления исследуемого круга.

2.5.    В качестве коллиматоров допускается использовать зрительные трубы геодезических приборов, имеющие фокусные расстояния и световые диаметры объективов, равные или большие чем у зрительной трубы исследуемого теодолита.

2.6.    При исследовании кругов теодолитов типов Т5 и ТЗО (ГОСТ 10529-70) зрительные трубы, используемые в качестве коллиматоров, должны иметь винтовые или оптические микрометры.

2.7.    Исследуемый теодолит должен быть установлен на устойчивом столбе, защищенном от толчков и сотрясений.

2.8.    При наведении на коллиматоры, образующие контрольный угол А зрительная труба теодолита должна быть установлена на бесконечность.

Освещенность сеток нитей коллиматоров и трубы теодолита должна быть одинаковой.

2.9.    Специальные марки, образующие контрольный угол А₉, должны быть установлены на расстоянии не менее 6 м от теодол*-

л — отсчет по кругу (или микрометру) при наведении зрительной трубы теодолита на левый коллиматор; п — отсчет по кругу (или микрометру) при наведении зрительной трубы теодолита на правый коллиматор;

Pj=nj—л₁—измеренное значение угла в первом полуприеме прямого хода;

г г г

р2^=п2—^л2 — измеренное значение угла во втором полуприеме прямого хода;

pj=n^——измеренное значение угла в первом полуприеме обратного хода;

ГОСТ 13424-68 Стр. 3

та. Разность расстояний до марок должна быть такой, чтобы при наведении на них не возникала необходимость в измерении фокусировки зрительной трубы теодолита.

Марки должны быть одинаковыми по форме и размерам и одинаково освещены.

2.10.    Установка коллиматоров (или марок) по высоте должна быть такой, чтобы во время измерений не возникала необходимость изменения положения зрительной трубы теодолита в вертикальной плоскости.

2.11.    Значения контрольных углов и интервалы между исследуемыми диаметрами кругов теодолитов разных типов должны соответствовать указанным в табл. 1.

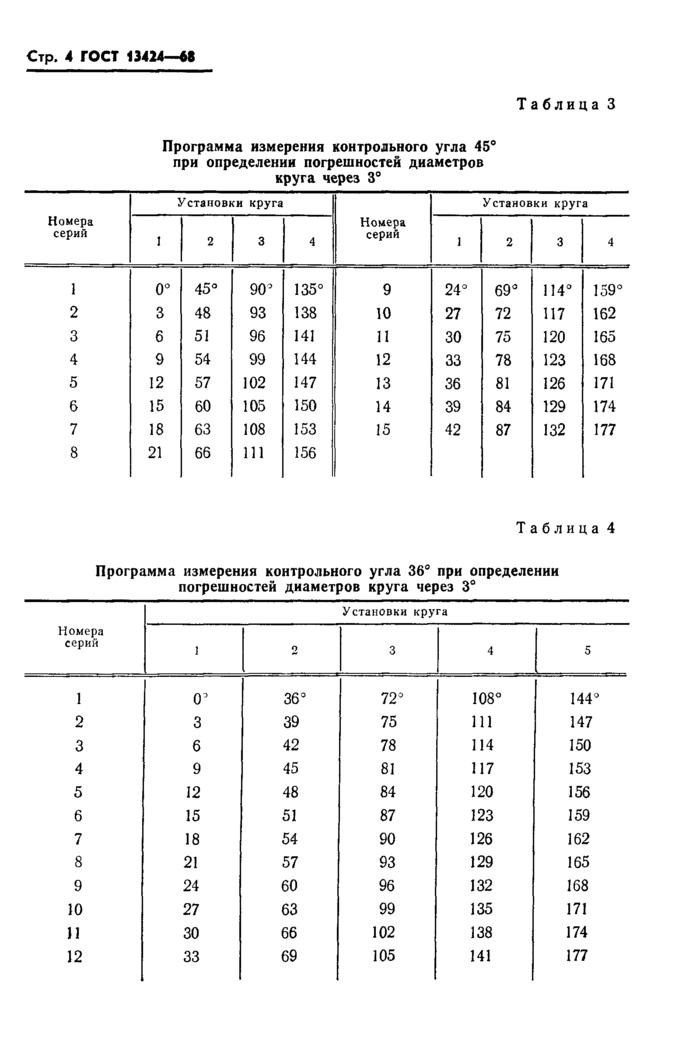
2.12. Измерения контрольных углов при исследовании лимба теодолита выполняют отдельными сериями по программам, указанным в табл. 2—7.

Таблица 3

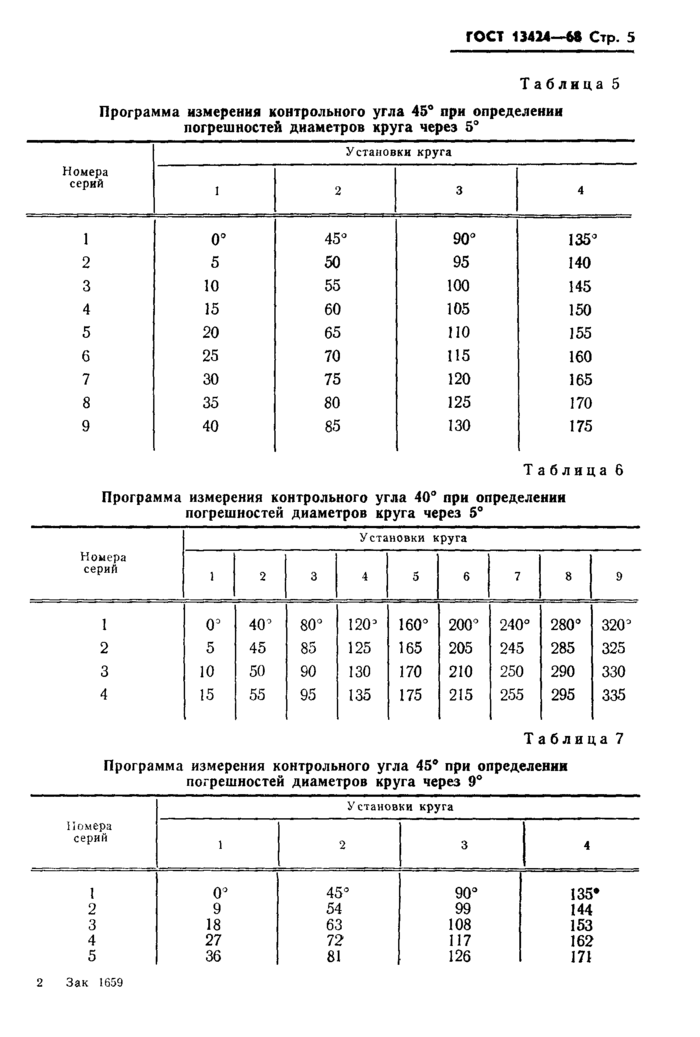
ГОСТ 13424--6$ Стр. 5

Стр. 6 ГОСТ 13424-68

2.13. Количество выполняемых серий измерений и количество перестановок поверяемого круга должны соответствовать указанным в табл. 8.

2.14.    В каждой серии измерения производят в прямом и обратном порядке, выполняя на каждой установке круга по одному приему в следующей последовательности:

Прямой ход

Первый полуприем 1—2;

Второй полуприем 2—1.

Обратный ход

Первый полуприем 2—1;

Второй полуприем 1—2. где 1 и 2 — наведения на левый и правый коллиматоры или марки.

2.15.    При измерениях углов, образующих одну серию, не допускается изменять фокусировку зрительной трубы теодолита, положение коллиматоров (или марок) и теодолита и освещение сеток нитей коллиматоров и зрительной трубы теодолита, а также поле зрения микроскопа теодолита.

В целях исключения систематической погрешности микрометра при измерениях в одной серии следует использовать примерно одну и ту же часть его отсчетной шкалы.

2.16.    При исследовании лимбов теодолитов с отсчетом по двум противоположным краям круга не допускается в процессе измерения углов переводить зрительную трубу через зенит.

У теодолитов с односторонним отсчетом кругов или с двусторонним отсчетом, но имеющих на лимбе две круговые шкалы, трубу через зенит переводят в каждом приеме.

2.17.    При исследовании кругов теодолитов с односторонним отсчетом точное наведение на нити сетки зрительной трубы производят с помощью винтового или оптического микрометров коллиматоров. В этом случае вместо отсчетов по кругу поверяемого

ГОСТ 13424-68 Стр. 7

теодолита в журнал записывают отсчеты по барабанам или шкач лам микрометров коллиматоров.

2.18.    Измерения контрольных углов при исследовании круга теодолита с односторонним отсчетом производят в следующем порядке.

2.18.1.    Снабженные микрометрами коллиматоры устанавливают так, чтобы их визирные линии составили угол А ₉ с вершиной, лежащей в точке установки исследуемого теодолита.

Зрительную трубу теодолита наводят на левый коллиматор, точно совмещая индекс отсчетного устройства исследуемого круга со штрихом а_у соответствующим начальной установке (например, 0°).

Пользуясь микрометром левого коллиматора, в биссектор сетки нитей (его зрительной трубы) вводят изображение вертикальной нити зрительной трубы теодолита и снимают отсчет с барабана или шкалы микрометра.

2.18.2.    Не изменяя положения исследуемого лимба, поворачивают алидаду теодолита, по ходу часовой стрелки и точно совмещают индекс со штрихом а+А_? .

При помощи микрометра зрительной трубы правого коллиматора в биссектор сетки нитей вводят изображение нити зрительной трубы теодолита и снимают отсчет с барабана или шкалы микроч метра.

2.18.3.    Зрительную трубу теодолита переводят через зенит и точно совмещают индекс со штрихом а+А₉ +180° (при этом труба теодолита будет наведена на правый коллиматор).

Микрометром правого коллиматора в биссектор его трубы вводят изображение вертикальной нити зрительной трубы теодо^ лита и снимают отсчет по барабану или шкале микрометра.

2.18.4.    Вращая алидаду против хода часовой стрелки точно совмещают индекс со штрихом а+180°.

Микрометром зрительной трубы левого коллиматора осуществляют точное наведение биссектора сетки его нитей на вертикальную нить зрительной трубы теодолита и снимают отсчет по барабану или шкале микрометра.

2 18.5. Указанные в пп. 2.18.1—2.18.4 действия составляют один прием.

На каждой установке круга исполняют по два приема.

2.18.6. Пример записи результатов измерений для теодолита с односторонним отсчетом приведен в приложении 1.

2.19.    В журнале для записи измерений контрольных углов записывают и вычисляют: измеренные значения углов; среднее арифметическое значение А₉ угла между коллиматорами, полученное

2*

Стр. 8 ГОСТ 13424-68

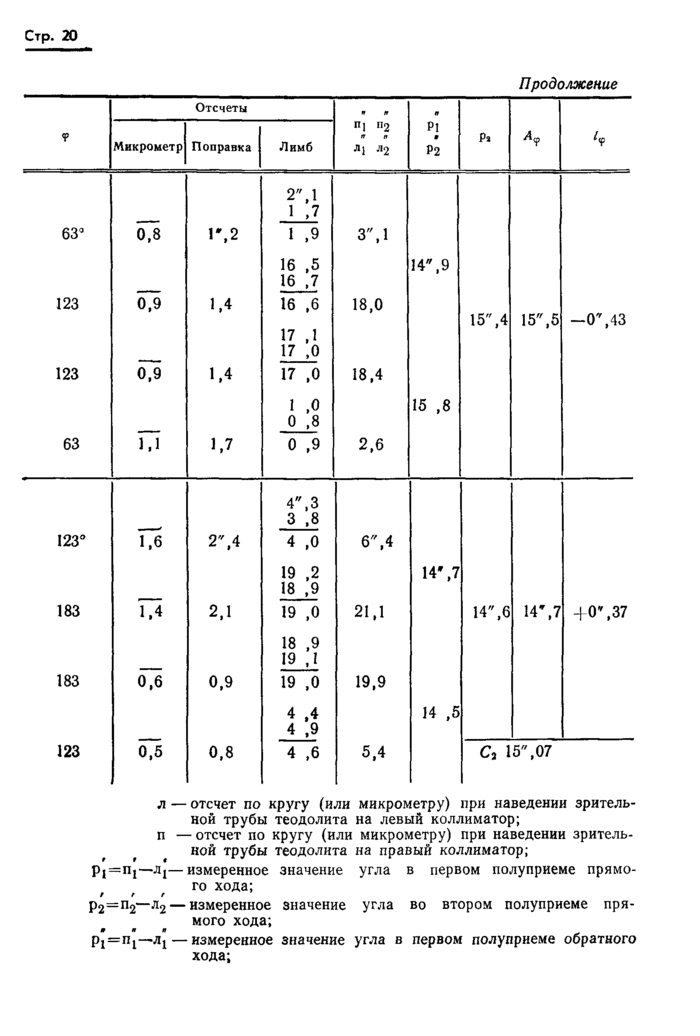
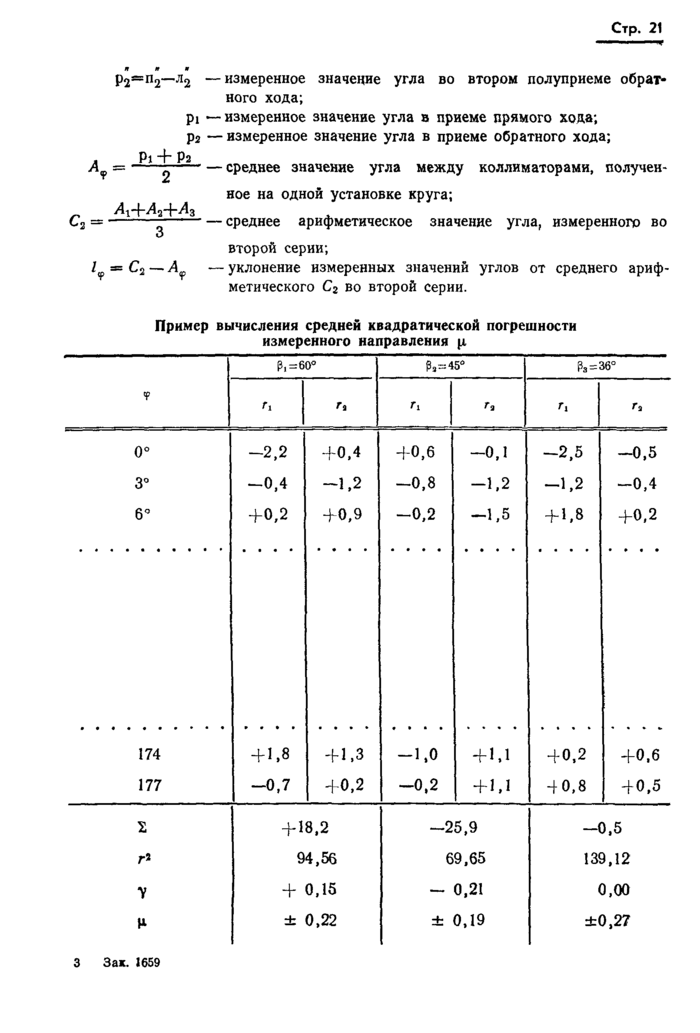
на одной установке круга; среднее арифметическое значение угла С из измерений в одной серии; отклонения измеренных значений углов /<р от среднего арифметического в каждой отдельной серии (l₉ =>Cj—A_f). По окончании программы наблюдений вычисляют также среднюю квадратическую погрешность (р) направления, измеренного в четырех полуприемах, по формуле

где г* — разность значений углов, измеренных в полуприемах прямого и обратного хода; п — общее число независимых установок круга, равное числу исследуемых диаметров; у — систематическая погрешность, вычисляемая по формуле

Ы_

2 п '

2.20. Средняя квадратическая погрешность (р) направления не должна превышать величин, указанных в табл. 9.

2.21. Пример записи в журнале наблюдений теодолита с двусторонним отсчетом и пример вычисления средней квадратической погрешности измеренного направления р приведены в приложении 2.

ГОСТ 13424-68 Стр. 9

3. СПОСОБЫ ВЫЧИСЛЕНИЯ ПОЛНЫХ ПОГРЕШНОСТЕЙ ДИАМЕТРОВ КРУГА

3.1. Вычисление полных погрешностей диаметров круга выполняют одним из способов, указанных в табл. 10.

3.2. В способах I и II значения полных погрешностей диаметров круга вычисляют из уравнений (3), решаемых под условием минимума суммы квадратов случайных погрешностей измерений. Уравнения погрешностей составляют по формуле

лс<р+(з .Хер — 1₉,    (3)

где -Сер и х₉₊$ — полные погрешности диаметров круга <р и <р+р;

4 — свободные члены уравнений погрешностей, вычисляемые по формуле U =    —А_уР.

Число уравнений погрешностей (3) равно числу измеренных углов А₉.

3.2.1. От уравнений погрешностей (3) переходят к нормальным уравнениям вида:

2_tXcp -^р+р! ■^'9 + Ра -^«р + Рз    • * •    *£(р + (10О°—pj)

-Х<р + (180°~р_а) —X<p+(180⁰-Pa) + ^<Р =0,    (4)

где Zi — коэффициент при квадратичном члене i-го нормального уравнения;

L₉—свободный член того же нормального уравнения, вычисляемый по формуле

£<р —+ 4 ^— 4 + ^80°-Pi) +    4V(180*-Pe) + 4^П+ 4+(180^в-Р*)| (5)

где Рь Р2, рз — номинальные значения первого, второго и третьего контрольных углов.