ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЛУЧИ КОСМИЧЕСКИЕ СОЛНЕЧНЫЕ
Вероятностная модель потоков протонов
Издание официальное
ГОССТАНДАРТ РОССИИ Москва
Предисловие
1 РАЗРАБОТАН Научно-нсслсловатсльскнм институтом ядерной физики Московского Госу-ларствснного Университета (НИИЯФ МГУ) и Всероссийским научно-исследовательским институтом стандартизации (ВНИИстанларт) Госстандарта России
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 27 апреля 2001 г. № 196-ст
3 ВВЕДЕН ВПЕРВЫЕ
© ИПК Издательство стандартов. 2001
Настояший стандарт нс может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Госстандарта России
II
Г О С У Д А Р С Т В Е Н Н Ы И СТЛНДЛ Р Г I» О С С И Й С К О Й Ф Е Д Е Р Л Ц И И
ЛУЧИ КОСМИЧЕСКИЕ СОЛНЕЧНЫЕ Вероятностная модель потоков протонов
Solar energetic particles. Probabilistic model for proton duxes
Дата ВВС.1СННЯ 2002—01—01
1 Область применения
Настоящий стандарт устанавливает вероятностные энергетические спектры потоков (флюсн-сон и максимальных пиковых потоков) протонов солнечных космических лучей (СКЛ) с энергией Е>5 МэВ в околотемном космическом пространстве вне магнитосферы Земли для условий изменяющегося уровня солнечной активности.
Стандарт предназначен для использования в расчетах радиационного воздействия протонов СКЛ на технические устройства, материалы и другие объекты в космическом пространстве.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ 25645.105-84 Лучи космические солнечные. Термины и определения
ГОСТ 25645.302-83 Расчеты баллистические искусственных спутников Земли. Методика расчета индексов солнечной активности
3 Определения
В настоящем стандарте применяют следующие термины с соответствующими определениями:
3.1 солнечные космические лучи (СКЛ): Потоки заряженных частиц высоких энергий (более 5 МэВ/нуклон) солнечного происхождения.
3.2 число Вольфа: Относительное число солнечных пятен, определяемое ежесуточно (ГОСТ 25645.302).
3.3 уровень солнечной активности: Среднегодовое или среднемесячное число Вольфа.
3.4 прогношруемыи уровень солнечной активности: Уровень солнечной активности, прогнозируемый от 4 месяцев до 11 лет вперед (но ГОСТ 25645.302).
3.5 солнечное протонное событие (СТ1С): По ГОСТ 25645.105.
3.6 флтснс прогонов: Полное количество протонов, падающих на сферу с сечением площадью I см2.
3.7 пиковый поток протонов: Максимальное количество прогонов, падающее в единицу времени в единице телесного угла на единичную площадку, перпендикулярную направлению наблюдения (в одном или нескольких событиях СКЛ. произошедших за определенный промежуток времени).
3.8 дифференциальный энергетический спектр флк>енса протонов: Дифференциальное распределение флюснса протонов по энергии.
3.9 дифференциальный энергетический спектр пикового потока протонов: Дифференциальное распределение пикового потока прогонов СКЛ по энергии.
3.10 вероятность фноенса: Вероятность, с которой флюснс протонов превышает заданное значение.
3.11 вероятность пикового потока: Вероятность, с которой пиковый поток протонов превышает заданное значение.
II панне официальное
4 Обозначения и сокращения
В настоящем стандарте применяют следующие сокращения и обозначения:
<1У> — среднегодовой уровень сашсчной активности;
< W*> — среднемесячный уровень солнечной активности;
Ф — флюснс протонов, ем-2;
Ф (>30) или Фад — значение события СКЛ;
Ф (£) — дифференциальный энергетический спектр флюснса прогонов. (см2МэВ) ';
/— пиковый поток протонов, см '2 ср”'-с_|;
/(£)—дифференциальный энергетический спектр (пикового) потока протонов. (см2срсМэВ)-1;
R — жесткость протона. МВ;
\10<? — энергия покоя протона, равная 938 МэВ:
D— спектральный коэффициент дифференциального энергетического спектра протонов;
Я. — спектральный индекс дифференциального энергетического спектра протонов;
6 — индекс завала спектра дифференциального энергетического спектра протонов;
</»> — ожидаемое в среднем количество событий СКЛ Фад> 105 см 2;
*Р — вероятность флюснса или пикового потока протонов превышать заданное значение;
|) — относительная скорость света;
£ — кинетическая энергия протона. МэВ.
5 Основные положения
5.1 Модель устанавливает в виде дифференциальных энергетических спектров значение флюенсов и пиковых потоков протонов, превышение которых в условиях заданного уровня солнечной активности <И/(/)> на временном интервале Тожидается с заданной вероятностью Ч*.
5.2 Дифференциальные энергетические спектры флюенсов |Ф (£)| или пиковых потоков [/■(£)! протонов (обобщенно F<£)| залают в форме степенных функций жесткости протонов R.
£,,.<£> rf£=0^j’,‘£. ("
где ц — спектральный индекс, при £>30 МэВ постоянен и равен X. а при £<30 МэВ р вычисляют по формуле
R — жесткость протонов, вычисляют по формуле
где £— кинетическая энергия протона. МэВ;
A/qC2 — энергия покоя протона, равная 938 МэВ:
/<, ■= 239 МВ. соответствует энергии протона £ =* 30 МэВ;
[5 — относительная скорость протона, которую вычисляют по формуле
р_ \/е\е + 2Д/Пс2) (4)
Е* J
5.3 Энергетические спсклзы (1) определяют, используя три параметра:
/)— снектр;иьный коэффициент;
л — спектральный индекс;
5 — индекс завала спектра.
Каждый из параметров является функцией двух параметров модели — среднего ожидаемого числа событий СКЛ </»> и вероятности 1Р.
5.4 К параметрам модели относятся:
- вероятность ‘Н превышения флюснса или пикового потока прогонов энергии £. задаваемого дифференциальным энергетическим спектром (1);
- среднее ожидаемое число событий СКЛ Ф^Ю5 см 2 — </»>.
5.5 Среднее ожидаемое число событий СКЛ Ф^Ю5 см-2 — </»> вычисляют по формулам: при продолжительности периода времени (длительность палета) Г<1 гол и равной т месяцам
т (5)
<я> = 0.27 -j- Л < \У]> .
где <W’t > — среднемесячные (прогнозируемые) числа солнечных пятен, при длительности полета Г >I гол и Г = s (лет) + т (месяцев)
I <»>
где < W> — среднегодовые (прогнозируемые) числа солнечных пятен, а отсчет гола начинают от момента начала интервала времени (начала полета).
5.6 Среднегодовые и среднемесячные числа солнечных пятен вычисляют по ГОСТ 25645.302-83.
5.7 Значения параметров дифференциальных энергетических спектров для флюснсов и пиковых потоков протонов Dr <я>, X* <н> и 6.,. <я> для набора наиболее часто встречающихся на практике параметров модели — вероятности 'И. равной 0.9:0.842:0.5:0.158; 0.1:0,05:0.0316; 0.01 и ожидаемых в среднем количеств событий <//>, равных I. 2. 4. 8, 16. 32. 64. 128. 256, 512. приведены в таблицах A.I—А.6 (приложение А). Параметры энергетических спектров для промежуточных значений параметров модели вычисляют по табличным данным методами интерполяции.
5.8 Подробная методика расчета флюснсов и пиковых потоков протонов, которая может быть использована для определения как дифференциальных энергетических спектров, так и промежуточных величин, необходимых для проведения некоторых специальных расчетов, приведена в приложении Ь.
6 Точность метода
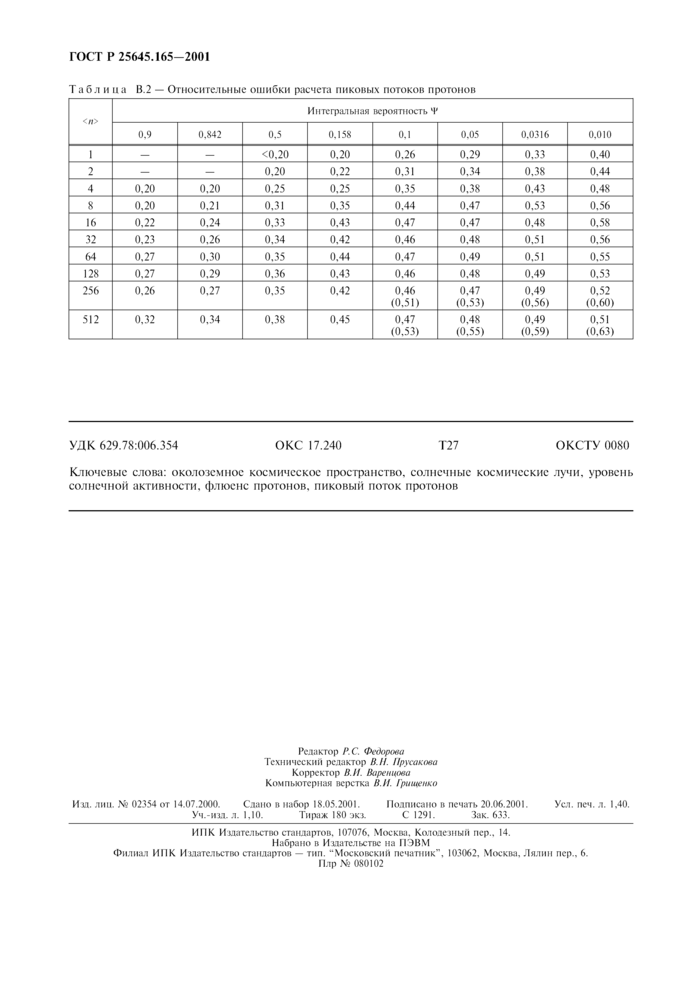
6.1 Точность метода характеризуется относительной погрешностью определения значений флюснсов и пиковых потоков, обусловленной ограниченной статистической точностью накопившихся к настоящему времени экспериментальных данных (таблицы B.I и В.2).
ПРИЛОЖЕНИЕ А (обязательное)
Таблицы параметров для расчета энергетических спектров флюенсов и пиковых потоков протонов
|
Т а б л и и а А. I — Коэффициенты дифференциального энергетического спектра флюенсов протонов А, <*> |
|
<п> |
А,. <я>, см-1, при нигегральиоП вероятности Ч* |
|
0.9 |
0.842 |
0.5 |
0.158 |
0.1 |
0.05 |
0.0316 |
0.010 |
|
1 |
— |
— |
0,6760 *-04 |
0.1340 06 |
0.3360 * 06 |
0.1030*07 |
0.1960*07 |
0.7810*07 |
|
2 |
— |
— |
0.3840+05 |
0.5050 + 06 |
0.1040+07 |
0.2770*07 |
0.5010+07 |
0.1530+08 |
|
4 |
0.I49E+05 |
0.2600 *05 |
0.I75E+06 |
0.1560+07 |
0,3070+07 |
0.696Е *07 |
0,1110+08 |
0.2620+08 |
|
8 |
0.93IE+05 |
0.I44E+06 |
0,7270+06 |
0,4450+07 |
0.7610*07 |
0.1470*08 |
0,2070+08 |
0.3970+08 |
|
16 |
0.4500+06 |
0,644Е+06 |
0.2400+07 |
0.1030+08 |
0.1640 *08 |
0.2650+08 |
0.3400+08 |
0.5580+08 |
|
32 |
0.I86E+07 |
0.248П <-07 |
0.7040+07 |
0.22IE+08 |
0.2980+08 |
0.4290 *08 |
0.523Е+08 |
0.7730+08 |
|
М |
0,648Е г 07 |
0.8100*07 |
0.1850*08 |
0.4210*08 |
0.5200 * 08 |
0,6860*08 |
0.7940 +08 |
0.1090 * 09 |
|
128 |
0,1980+08 |
0.2360 f 08 |
0.4350*08 |
0.7710*08 |
0.9050 * 08 |
0.11 IE *09 |
0,1230 09 |
0.1530*09 |
|
256 |
0.539Е+08 |
0.6160*08 |
0,9380+08 |
0.1410*09 |
0.1570*09 |
0.1790*09 |
0.1950+09 |
0.2250+09 |
|
512 |
0.I35E+09 |
0.1470*09 |
0,1950+00 |
0.2570 + 09 |
0.2760 * 09 |
0.300Е *09 |
0.3I8E+09 |
0.3450*09 |
|
|
Табл и на А.2 — Индексы дифференциального энергетического спектра флюенсов протонов >-*.<*> |
|
<п> |
*+ <*• ПР*' интегральной вероятности 4’ |
|
0.9 |
0.842 |
0.5 |
0.158 |
0.1 |
0.05 |
0.0316 |
0.010 |
|
1 |
— |
— |
6.41 |
5.18 |
4.86 |
4.48 |
4.29 |
4.12 |
|
2 |
— |
— |
5.64 |
4.74 |
4.50 |
4.30 |
4.19 |
4.03 |
|
4 |
6,15 |
5.91 |
5.19 |
4.46 |
4.29 |
4.19 |
4.11 |
3.94 |
|
8 |
5.60 |
5.46 |
4.81 |
4.28 |
4.18 |
4.10 |
4.02 |
3.86 |
|
16 |
5,19 |
5,05 |
4.52 |
4.18 |
4.11 |
4.02 |
3,95 |
3.79 |
|
32 |
4.83 |
4.70 |
4.36 |
4,13 |
4.04 |
3.95 |
3.88 |
3.73 |
|
64 |
4.56 |
4.48 |
4.27 |
4.05 |
3.98 |
3.90 |
3.84 |
3.69 |
|
128 |
4.41 |
4.37 |
4.20 |
4.01 |
3.95 |
3.87 |
3.81 |
3.67 |
|
256 |
4.31 |
4.28 |
4,14 |
3.99 |
3.93 |
3.85 |
3.81 |
3.67 |
|
512 |
4,24 |
4.21 |
4,10 |
3,96 |
3.91 |
3.84 |
3.81 |
3.68 |
|
ГОСТ 1* 25645.165-2001
|
I а б л и па А.З — Индексы завала дифференциального энергетического спектра фыюенсов протонов гя> |
|
<п> |
<V <*> при интегральной вероятности Ч* |
|
0.9 |
0.842 |
0.5 |
0.158 |
0.1 |
0.05 |
0,0316 |
0.010 |
|
1 |
— |
— |
0.168 |
0.055 |
0.050 |
0.049 |
0.054 |
0.078 |
|
2 |
— |
— |
0.076 |
0.048 |
0.048 |
0.057 |
0.071 |
0.089 |
|
4 |
0.122 |
0.085 |
0.062 |
0.049 |
0.059 |
0.074 |
0.085 |
0.086 |
|
8 |
0.077 |
0.069 |
0.050 |
0.062 |
0.072 |
0.084 |
0.084 |
0.069 |
|
16 |
0.058 |
0.053 |
0.048 |
0.067 |
0.070 |
0.081 |
0.076 |
0.052 |
|
32 |
0.048 |
0.046 |
0.050 |
0.064 |
0.065 |
0.066 |
0.059 |
0.032 |
|
64 |
0.045 |
0.046 |
0.057 |
0.064 |
0.060 |
0.054 |
0.046 |
0.019 |
|
128 |
0.049 |
0.052 |
0.059 |
0.056 |
0.052 |
0.042 |
0.034 |
0.009 |
|
256 |
0,053 |
0.055 |
0.056 |
0.049 |
0.043 |
0.032 |
0.025 |
0.004 |
|
512 |
0.055 |
0.056 |
0.053 |
0.043 |
0.036 |
0.025 |
0.017 |
0.000 |
|
|
Г а 6л н и а Л.4 — Ко ><|к|»|1нис11 гы дифференциального энергетического спектра пиковых потоков протонов
<я> |
|
<п> |
Л*.<*>* (смгср с МэВ)-'. при нктсгралыюП всроягносги *Р |
|
0.9 |
0.842 |
0.5 |
0.158 |
0.1 |
0.05 |
0.0316 |
0.010 |
|
1 |
— |
— |
0.0014 |
0.056 |
0.170 |
0.750 |
1.66 |
8.4 |
|
2 |
— |
— |
0.0106 |
0.261 |
0.706 |
2.35 |
4.75 |
20.8 |
|
4 |
0.00257 |
0.0041 |
0.0561 |
1 |
2.27 |
6.65 |
12 |
39.6 |
|
8 |
0.0159 |
0.0237 |
0.258 |
3.24 |
6.75 |
16.7 |
26.8 |
77.5 |
|
16 |
0.0866 |
0.123 |
1 |
8.56 |
15.9 |
32.7 |
50.6 |
126 |
|
32 |
0.389 |
0.537 |
3.27 |
19.9 |
32.9 |
63.4 |
89.9 |
215 |
|
64 |
1.48 |
1.94 |
8.86 |
40 |
60.3 |
104 |
145 |
300 |
|
128 |
4.33 |
5.45 |
20.6 |
70.3 |
102 |
171 |
227 |
425 |
|
256 |
11.3 |
13.8 |
41 |
116 |
169 |
264 |
332 |
540 |
|
512 |
26.8 |
31.5 |
73.6 |
191 |
252 |
370 |
446 |
702 |
|
|
Т а б л и н а А.5 — Индексы дифференциального энергетического спектра пиковых потоков протонов /.* ^ |
|
<я> |
Ку гя> при интегральном вероятности Ч* |
|
0.9 |
0.842 |
0.5 |
0.158 |
0.1 |
0.05 |
0.0316 |
0.010 |
|
1 |
6.779 |
6.581 |
6.434 |
5.09 |
4,765 |
4.413 |
4.247 |
4.06 |
|
2 |
8.071 |
6.976 |
5.548 |
4.672 |
4.433 |
4.23 |
4.134 |
3.98 |
|
4 |
6.065 |
5.872 |
5.083 |
4.348 |
4.24 |
4.131 |
4.05 |
3.889 |
|
8 |
5.415 |
5.306 |
4.664 |
4.219 |
4.129 |
4.041 |
3.956 |
3.814 |
|
16 |
4.943 |
4.841 |
4.369 |
4.11 |
4.052 |
3.%1 |
3.9 |
3.765 |
|
32 |
4.567 |
4.491 |
4.195 |
4.02 |
3.948 |
3.883 |
3.822 |
3.72 |
|
64 |
4.2% |
4.262 |
4.107 |
3.935 |
3.87 |
3.81 |
3.756 |
3.649 |
|
128 |
4.164 |
4.145 |
4.028 |
3.869 |
3.806 |
3.754 |
3.699 |
3.6 |
|
256 |
4.098 |
4.092 |
3.%2 |
3.82 |
3.773 |
3.704 |
3.63 |
3,52 |
|
512 |
4.069 |
4.057 |
3.885 |
3.777 |
3.685 |
3.613 |
3.568 |
3.44 |
|
|
Табл и на А.6 — Индексы завала дифференциального энергетического спектра пиковых потоков протонов (Ц, <л> |
|
<я> |
при интегральной вероятности Ч* |
|
0.9 |
0.842 |
0.5 |
0.158 |
0.1 |
0.05 |
0.0516 |
0.010 |
|
1 |
— |
— |
0.167 |
0.065 |
0.064 |
0.080 |
0.089 |
0.121 |
|
2 |
— |
— |
0.078 |
0.069 |
0.078 |
0.100 |
0.1 II |
0.135 |
|
4 |
0.12 |
0.095 |
0.064 |
0.083 |
0.095 |
0.122 |
0.132 |
0.147 |
|
8 |
0.07 |
0.068 |
0.066 |
0.110 |
0.127 |
0.142 |
0.150 |
0.152 |
|
16 |
0.064 |
0.063 |
0.084 |
0.132 |
0.145 |
0.155 |
0.158 |
0.155 |
|
32 |
0.072 |
0.075 |
0.108 |
0.151 |
0.156 |
0.158 |
0.152 |
0.153 |
|
64 |
0.093 |
0.099 |
0.134 |
0.163 |
0.154 |
0.152 |
0.145 |
0.137 |
|
128 |
0.111 |
0.131 |
0.151 |
0.159 |
0.156 |
0.152 |
0.142 |
0.124 |
|
256 |
0.156 |
0.168 |
0.170 |
0.156 |
0.159 |
0.155 |
0.140 |
0.107 |
|
512 |
0.188 |
0.197 |
0.180 |
0.165 |
0.159 |
0.152 |
0.143 |
0.090 |
|
ПРИЛОЖЕНИЕ В (справочное)
Методика расчета флюснсов и пиковых потоков протонов
БЛ Значения флюс псов и пиковых потоков протонов, превышение которых ожидается с заданной вероятностью 4*. для условии заданного уровня солнечной активности <1У> на временном интервале Т вычисляют по расчету потоков протонов для батыного количеств;» вариантов полета /V с последующим преобразованием вычисленных вероятностных кривых в энергетические спектры.
Рашыс варианты полетов отличаются:
а) разным «случайным» количеством событий СКЛ (при заданном среднем <я>);
б) величина каждого из событий Ф«, является «случайной» в рамках функции распределения;
в) значения параметров энергетического спектра протонов (спектральный индекс у и индекс завала спектра а) для каждого события при случайной величине Ф10 также являются «случайными» и заданы средними значениями и их статистическими отклонениями.
Б.2 Расчет флюснсов и пиковых потоков протонов, превышение которых ожидается с заданной вероятностью Ч\ для условий заданного уровня солнечной активности <1У> на временном интервале Г:
1. Вычисляют основной параметр модели — среднее ожидаемое количество событии СКЛ Фм к 10-' см-2 <я> по формулам (5) или (6) настоящего стандарта.
2. Вычисляют флюенсы или пиковые потоки для N случайных вариантов полета при рекомендуемом значении ;V к 30000.
Б.2.1 Для каждого варианта вычисляют случайное количество событий СКЛ я.
Если <л> мало (<я> <8). то для определения случайного числа событий следует пользоваться распределением Пуассона, для которого при средней величине <я> вероятность наблюдать я событий равна
схр (—<Я>) <Я>* Р (я,<я>) =-—}-
т. е. вычисляют случайные значения флюенсов и пиковых потоков для К„ = Spin. <я>) вариантов палета с количеством событий я ■ 0, I. 2. 3 и т. д.
Если <я> > 8. то для определения я (случайного числа событий для каждого очередного варианта полета) следует пользоваться методом Монте-Карло согласно нормальному (Гауссову) распределению
Б.2.2 Вычисляют елейную величину Ф$ каждого события / (10's Фи, £ 10") протонов/см2 метолом Мойте-Kapiio и» распределения
Б.2.3 Для каждого события / величиной Ф',',1, вычззеляюг «случайные» параметры дифференциальных энергетических спектров (спектральный индекс и индекс завала спектра «). заданных в виде степенных спектров по жесткости с завалом в области низких энергий (£<30 М эВ>
а при £<30 М эВ т=1,°(^оГ
где Лир — жесткость зз относителызая скорость протона, определяемая по формулам (3) зз (4) настоящего стандарта.
За исключением спсктральз1ых коэффиниеззгов С. велич131зы у0 и « как для лнффсрсззнзза1ьв1ых эззерге-ттзческнх спектров флюеззеов (Фз. гак и для пиковых потоков (/) протонов принимают одинаковыми.
Б.2.3.1 Используя значение события Ф$, определяют среднее зиачеззие спектрального иззлекса диз)к)>с-рензизалызого энергетического спектра прогонов ’>
<Х{,' *> = 6.3
< К> = 5.5 - 0.8 sin|- (log (ф^)-7)| <^о *> 4.7
при Фад < I06 протоззов/см2 (Б.5а)
при IО6 ^ ^ 10х протонов/см2 (Б.5Ь)
при Ф'^ > 10х протонов/см2. (Б.5с)
Находят стандартное отклонение логнормального распределения
%., = 0.023 <7(>>
Методом Монте-Карло находят случайную величину спектратыюго индекса энергетического спектра флюенсов протонов в событии ‘ в предположении, что случайные величины спектрального иззлекса
раеззределены логнормально вокруг среднего <Х^ ’>.
Б.2.3.2 Используя величн1зу собыгззя Ф1^' и спектрального индекса Х^1, определяют средний индекс заззала <аи ,>
I6LsK_f,e.
• (8.6 !()«•] (4.5J '
Стандартное отклонение 1ззздекса завала спектра протонов о|' \t вычисляют по формуле
<С-0-2
|
гле |
в =
и — |
3 I07 |
|
и |
п — |
ф'>
м |
|
.36 |
При Фад 2: 3-I07 протонов/см2 при < 3 107 протонов/см2.
Далее метолом Монте-Карло находят случайное зззачеззие иззлекса завала а*' ► дззфз]>срсз1зизальззого энергетического спектра протоззов из логнормальзюго распрслслснззя случайных величин;
Б.2.3.3 Спектральный коэз]эфииззснт лнфференииалызого эззсргетичсского спектра флюеззеов протонов С'ф вычисляют по формуле
(Б.9)
Б.2.3.4 Среднее значение спектрального коэффициента дифференциального энергетического спектра пиковых потоков протонов С"' ВЫЧИСЛЯЮТ ПО формуле
<С<?Ь» - 6.0 10-’ (фдаУ'да протонов/(см2ср-с-МэВ). <Б,,0)
Стандартое отклонение для логнормального распределения спектральных коэффициентов пиковых потоков протонов принимают равным
0|g “ 0,5. (Б.II)
Далее метолом Монте-Карло вычисляют случайное значение спектрального коэффициента дифференциального энергетического спектра пикового потока протонов C'j \ следуя логнормальному распределению.
Б.2.4 По формулам (Б.4) и (Б.5) вычисляют энергетические спектры флюенсов тан пиковых потоков для каждого случайного события.
Б.2.4.1 Параметры С“\ У'\ о"1 используют для вычисления дифференциального энергетического спектр;! флюенсов протонов СКЛ Ф" ’(А ) для случайного события СКЛ / (I й / </»).
Б.2.4.2 Параметры C"F'. Vм. at1* используют для вычисления дифференциального энергетического спектра пиковых потоков протонов СКЛ /" •(Е ) для случайного события СКЛ / (I 5 i <, я).
Б.2.4.3 Для каждого события СКЛ вычисляют интегралы1ые энергетические спектры флюенсов Ф" Ч2 Е) и пиковых потоков/*' ►(£ Е )
Ф"><*£) = /Ф»Ч£>з/£ /<'><г £> = //«><£)</£. (Б.12)
£ £
Б.2.5 Определив энергетические спектры для каждого из л случайных событии, вычисляют энергетические спектры флюенсов и пиковых потоков для каждого варианта палета.
Б.2.5.1 Вычисляют интегральный энергетический спектр флюенсов протонов Фт (2 £) для каждого варианта полета т (I £ т й >V). суммируя флюснсы Ф" > (г £ ) всех л событий
#»
<*«ftfl = l4"'ft£). <Б|3>
Б.2.5.2 Интегральный энергетический спектр пиковых потоков протонов для каждого вариатгта полета /<2: Е ) находят, выбирая из пиковых потоков п событий максимальные потоки при каждой энергии Е:
/(£ £) « max [f{i ’(* £ )J . (Б. 14)
Б.З Определяют энергетические спектры флюенсов и пиковых потоков протонов для всех N вариантов полета и вероятности иметь флюснс или пиковый поток протонов больше заданной энергии £в выбранном интервале Фт(2 Е ) ♦ Фт+|(а Е ). или £ ). или интегральные вероятности иметь флюенс или
пиковый поток протонов больше заданной энергии А'выше заданного значения флюенса Фм(а А ) или пикового потока /Да Е).
Б.З. 1 Для определения плотности вероятности находят относительное количество вариантов sm из N вариантов полета, флюенс или пиковый поток которых для протонов энергии больше А'находится в интервалах ЛФ,„(£ £ ) и Е) соответственно:
ЛФ*(^ £) = Фти <* £) - Ф*<* £) или &£)»/„., ft £)-/„&£) (Б. 15)
ДЧ'(Ф1П) = 3Л/;У или AW{fm) = Sm/N. (Б. 16)
, d'Y
или соответствующие плотности вероятности флюенсов
d'Y
или пиковых потоков (lj r, у>:
d'Y , d'Y 5 (Б.17)
</ф(а£) Л'дФтгА ) или dfa> £) Щ7ПГ)'
Формула (Б. 17) является вероятностью иметь при заданных условиях палета флюенс или пиковый поток протонов с энергией больше А'в интервале (Б. 15).